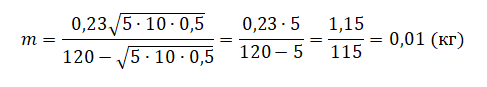Задание ЕГЭ-Ф-ДВ2023-30(1)

Алгоритм решения:

Решение:

Запишем исходные данные:

Переводим единицы измерения величин в СИ:

M = 230 г = 0,23 кг

l = 50 см = 0,5 м

Систему отсчёта, связанную с Землёй, будем считать инерциальной. Тела считаем материальными точками.

Для описания взаимодействия пули и шара используем закон сохранения импульса системы тел. Он выполняется в инерциальной системе отсчёта, если сумма внешних сил, приложенных к телам системы, равна нулю. В данном случае проекции внешних сил (силы тяжести и силы натяжения нити) на горизонтальную ось в момент взаимодействия равны нулю. Следовательно, можно использовать закон сохранения импульса в проекциях на эту ось.

Для дальнейшего движения шара с застрявшей в нём пулей будет справедлив закон сохранения механической энергии, поскольку сопротивлением воздуха по условию задачи можно пренебречь, а единственная неконсервативная сила, действующая на шар, – сила натяжения нити – не совершает работы при движении шара по окружности, поскольку она всюду перпендикулярна скорости движения шара.

Условие минимальности v₀ означает, что шар совершает полный оборот в вертикальной плоскости, но при этом натяжение нити в верхней точке (и только в ней) равен 0.

Применим закон сохранения импульса, согласно которому сумма импульсов всех сил в системе не меняется до и после их взаимодействия. Следовательно:

Так как начальная скорость V шара равна нулю:

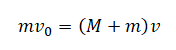
Скорость v — скорость движения шара и пули, которые после столкновения движутся как единое тело с массой M + m.

Теперь применим закон сохранения энергии. Учитываем, что в момент столкновения система тел имела максимальную скорость, а соответственно — максимальную кинетическую энергию. Также учитываем, что в верхней точке движения кинетическая энергия системы тел была меньше за счет уменьшения скорости, но не была нулевой. Также в верхней точке траектории система тел обладала максимальной потенциальной энергией. Запишем это так:

Максимальная кинетическая энергия системы тел будет равна:

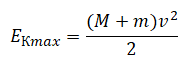
Кинетическая энергия в верхней точке:

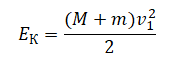
v₁ — скорость системы тел в верхней точке.

Потенциальная энергия равна произведению массы системы тел на ускорение свободного падения и на высоту, на которой находится система в верхней точке — h. Эта высота равна удвоенной длине нити:

Тогда закон сохранения энергии принимает вид:

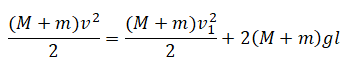
Также применим законы Ньютона к системе тел в верхней точке траектории. С одной стороны, на нее действует сила тяжести $F_{тяж}=\left(M+m\right)g.$ С другой — центробежная сила — $F_{Ц}=\frac{(M+m)v_1^2}{l}$. В знаменателе используем длину нити, так как она в данном случае равна радиусу окружности, по которой происходит движение системы тел.

Модули этих сил равны. Следовательно:

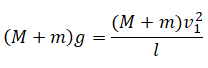
Или:

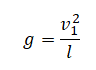
Отсюда выразим квадрат скорости в верхней точке:

Подставляем это выражение в закон сохранения энергии:

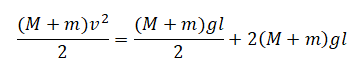
Или:

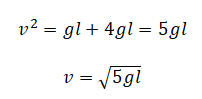
Подставляем эту скорость в закон сохранения импульса и выразим из него массу пули:

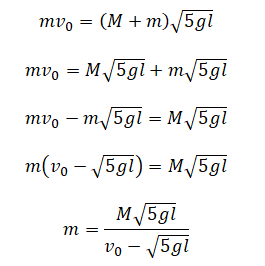
Подставляем известные значения и находим массу пули: