Задание №1 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.
Задание EF18273
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17519
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
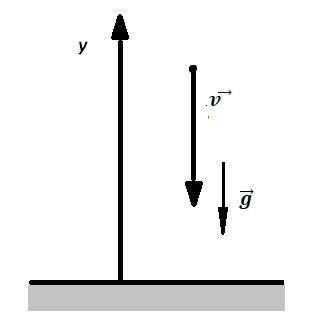
Перемещение (высота) свободно падающего тела, определяется по формуле:
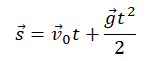
В скалярном виде эта формула примет вид:
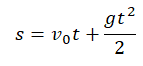
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
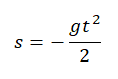
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
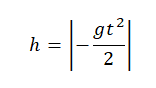
Вычисляем высоту, подставив известные данные:
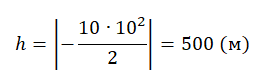
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
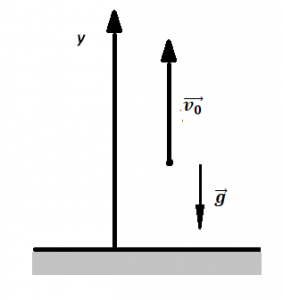
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17957
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения пути при равноускоренном прямолинейном движении.
- Определить недостающие исходные данные.
- Найти искомую величину.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Конечная скорость v = 20 м/с.
- Время изменения скорости t = 10 с.
Формула для вычисления пути при равноускоренном прямолинейном движении:
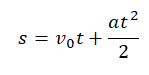
Так как начальная скорость равна нулю, формула принимает вид:
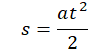
Нам неизвестно ускорение, но его можно вычислить по формуле:
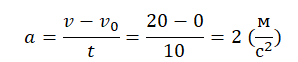
Вычисляем путь:
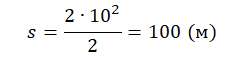
Ответ: 100
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17553
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…

Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831

Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1 и s2, а затем сложим их:

s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17612
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид:

Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17727
Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно оси ОХ: v1 = v.
- Скорость второго автомобиля относительно оси ОХ: v2 = –4v.
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость второго автомобиля относительно оси ОХ (v2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
v2 = v + v1
Отсюда:
v = v2 — v1 = –4v – v = –5v
Ответ: -5vpазбирался: Алиса Никитина | обсудить разбор
Задание EF17518
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей в скалярном виде.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно неподвижной системы отсчета: v1 = 110 км/ч;
- Скорость второго автомобиля относительно Земли: v2 = 60 км/ч.
Изображаем графическую модель ситуации:
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость автомобиля относительно земли (v1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v2).
По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
v’ = v + u
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
v = v’ — u = v1 — v2 = 110 – 60 = 50 (км/ч).
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.
Ответ: 50pазбирался: Алиса Никитина | обсудить разбор
👀 35.5k

хорошие задания -но я непонимаю-во второй задаче по системе СИ я перевел 30 км и получил 30000 м и 0,5 ч перевел в 1800сек и у меня стал неверный ответ.Почему?
Александр, нужно просто посмотреть, в каких единицах требуют ответ. В заданиях такого типа чаще всего необходимо указать в форме км/ч. В м/с ответ будет 16,666 что тоже верно, но это уже другие величины.
привет из 2020
В этом году обновим раздел! =)
Невозможно правильно решить задачу на «ускорение»,пока не определитесь: что такое скорость «at», и скорость «2at».
Скорость at-это равномерное движение-(СРЕДНЯЯ скорость, V начальное=V конечной).
Средняя скорость (у «яблока…») соответствует этим требованиям:- движение равномерное, нач.и кон. скорости равны: 4,9…м/с. Это «at». «Конечная скорость» НЕ есть «at», т.к. её нач. скорость=0, а конечная=9,8..м/с.
«Если тела прошли путь S за одинаковое время t — Средняя скорость и ускорение будут одинаковы, в независимости от графиков их движения». Самое главное: СИЛА, обеспечивающая это движение, (с любым графиком) будет ОДИНАКОВА и ускорение будут равны, т.к. S/tt- это «прибавка скорости к скорости», а F/m- это «энергия движения». И они- РАВНЫ! (1 литр воды=одному кг. воды). Расчёты можно вести в разных системах.
S,t,m можно измерить . Искать просто ускорение-бессмысленно. Задача: найти СИЛУ движения! И «а» S/tt = «а» F/m. S/tt=F/m. ВСЁ! Теперь можно найти и силу ,и КПД механизма (мотора у машины, или ракеты).
…Инженерам тех. задание: сделать машину массой не более 1200 кг., с разгоном не более 22 сек. Какой мощности нужен мотор? S/tt (V средняя!)/t=F/m. 13,9/22=F/1170. F=739 кг..м/сс. Это 9,85 л.с. при 100% КПД. КПД двс=16% (у ВСЕХ бензиновых ДВС ) 9,85*6,25=61,6 л.с. Получилось «Жигули 2101».
Для разгона за 18 сек. нужен мотор 75 л.с. (3-я модель «Жигули).
Если хотим машину с разгоном…9 сек. с такой массой, нужен мотор: 13,9/9=F/1170. F=150,5 л.с.
«Ускорение»- это «золотой ключик» для S,t,m,v,V,КПД,n,F…!!!
очень дюступно