Задание №32 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Для решения задания № 32 могут потребоваться знания из разных разделов физики. Как правило, в рамках одной задачи перекликаются материалы из 2-4-х разделов. В разделе теории приведены сведения, которые могут потребоваться при решении, но не были рассмотрены в теоретических разделах других задач по соответствующим тематикам.
Задание EF15717
Алгоритм решения
Решение
Запишем исходные данные:
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
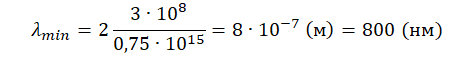
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18201
Излучением лазера с длиной волны 3,3⋅10−7 м за время 1,25⋅104 с был расплавлен лёд массой 1 кг, взятый при температуре 0 °С, и полученная вода была нагрета на 100 °С. Сколько фотонов излучает лазер за 1 с? Считать, что 50% излучения поглощается веществом.
Алгоритм решения
Решение
Запишем не только те данные, что есть в условии задачи, но и табличные данные, которые нам понадобятся в ходе решения задачи:
Чтобы лед расплавился, а образовавшаяся вода нагрелась до температуры кипения, нужно сообщить ему следующее количество энергии:
Q=Q1+Q2=mλльда+mc(t2−t1)
Так как КПД равен 50% (0,5), то это количество теплоты равно половине энергии, выделенной лазером:
Q=ηE
mλльда+mc(t2−t1)=ηE
Энергия, выделенная лазером, равна сумме энергий каждого из излученных фотонов, количество которых будет равно N:
E=Nhν
Но частота световой волны равна:
ν=cλсвета
Тогда:
E=Nhcλсвета
Отсюда:
Nhcλсвета
Теперь мы можем записать:
mλльда+mc(t2−t1)=ηNhcλсвета
Выразим количество излученных фотонов за все время:
N=λсвета(mλльда+mc(t2−t1))ηhc
Если разделить это выражение на время проведения опыта, то мы найдем количество фотонов, излученных за 1 секунду:
N1с=λсвета(mλльда+mc(t2−t1))ηhct
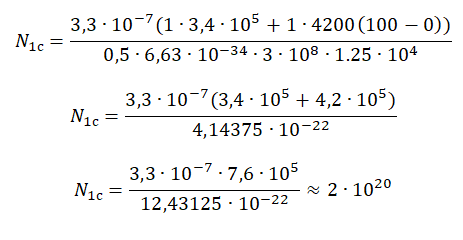
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17726
Покоящийся атом излучает фотон с энергией 16,32·10–19 Дж в результате перехода электрона из возбуждённого состояния в основное. Атом в результате отдачи начинает двигаться поступательно в противоположном направлении с кинетической энергией 8,81·10–27 Дж. Найдите массу атома. Скорость атома считать малой по сравнению со скоростью света.
Алгоритм решения
Решение
Запишем исходные данные:
Так как до излучения фотона атом покоился, то его импульс был равен нулю. Поэтому после излучения фотона суммарный импульс согласно закону сохранения импульса тоже должен быть равен нулю. Поэтому импульс атома равен по модулю импульсу излученного фотона:
pа=pф
Импульс тела и его кинетическая энергия — связанные величины. Но скорость атома много меньше скорости света. Поэтому для атома связь импульса с кинетической энергией будет описываться нерелятивистским выражением:
Eа=p2а2mа
Отсюда импульс, обретенный атомом, равен:
pа=√2mаEа
Фотон двигается со скоростью света, и его импульс может быть выражен из следующей его связи с энергией:
Eф=pфc
Тогда импульс фотона равен:
pф=Eфc
Приравняем импульсы атома и фотона:
√2mаEа=Eфc
Возведем обе части выражения в квадрат, выразим и посчитаем массу атома:
2mаEа=E2фc2
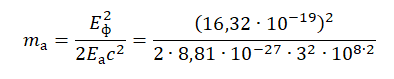
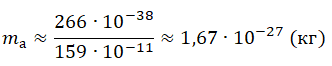
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17552
Пациенту ввели внутривенно дозу раствора, содержащего изотоп 1124 Na. Активность 1 см3 этого раствора а0 = 2000 распадов в секунду. Период полураспада изотопа 1124 Na равен T = 15,3 ч. Через t = 3 ч 50 мин активность 1 см3 крови пациента стала а = 0,28 распадов в секунду. Каков объём введённого раствора, если общий объём крови пациента V = 6 л? Переходом ядер изотопа 1124 Na из крови в другие ткани организма пренебречь. Ответ записать в куб. см.
Алгоритм решения
Решение
Запишем исходные данные:
Переведем объем крови пациента в кубические сантиметры, так как активность раствора и крови рассчитывается на 1 куб. см:
6 л = 6000 куб. см
Период полураспада и время переведем в секунды:
15,3 ч = 15,3∙60∙60 = 55080 с
3 ч. 50 мин = 3∙60∙60 + 50∙60 = 13800 с
Запишем закон радиоактивного полураспада:N=N0·2−tT
Объем введенного раствора обозначим за V0. Изначально активность всего объема крови пациента будет равна активности введенного раствора. Следовательно:
at=0=a0(V01 см3)
Тогда активность 1 куб. см крови в начальный момент времени будет равна:
a1=a0(V01 см3)(1 см3V)=a0V0V
По закону радиоактивного распада по прошествии времени t активность 1 куб. см крови станет равной:
a=a1·2−tT
Подставим сюда найденное раннее выражение:
a=a0V0V·2−tT
Выразим объем раствора:
a=a0V0V·2−tT
V0=aVa02−tT=aV2tTa0
Вычислим:
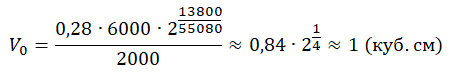
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
Решение
Запишем исходные данные:
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
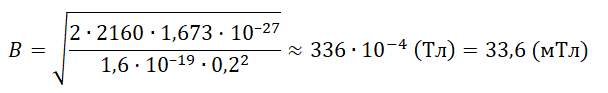
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18703
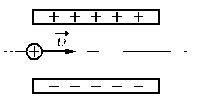 Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.
Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.
Алгоритм решения
Решение
Запишем исходные данные:
1 см = 0,01 м
5 см = 0,05 м
Сделаем рисунок:
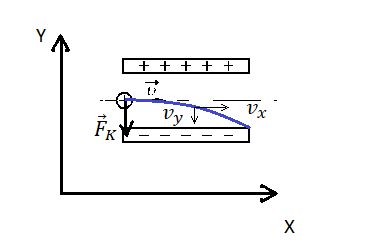
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
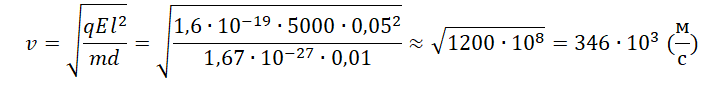
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350pазбирался: Алиса Никитина | обсудить разбор
Задание EF17550
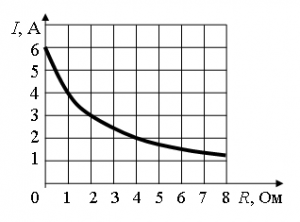 Реостат R подключен к источнику тока с ЭДС E и внутренним сопротивлением r (см. рисунок). Зависимость силы тока в цепи от сопротивления реостата представлена на графике. Найдите сопротивление реостата, при котором мощность тока, выделяемая на внутреннем сопротивлении источника, равна 8 Вт.
Реостат R подключен к источнику тока с ЭДС E и внутренним сопротивлением r (см. рисунок). Зависимость силы тока в цепи от сопротивления реостата представлена на графике. Найдите сопротивление реостата, при котором мощность тока, выделяемая на внутреннем сопротивлении источника, равна 8 Вт.
Алгоритм решения
Решение
Запишем исходные данные:
Мощность тока, выделяемая на внутреннем сопротивлении источника, определяется формулой:
Pвнутр=(εR+r)2r
Выразим отсюда сопротивление реостата:
R=ε√rPвнутр−r
Запишем закон Ома для полной цепи:
I=εR+r
Согласно графику, при нулевом сопротивлении реостата, сила тока, равна 6 Амперам. Следовательно:
I(0 Ом)=εr=6
Но при сопротивлении реостата в 4 Ом сила тока равна 2 Амперам. Следовательно:
I(4 Ом)=ε4+r=2
Получили систему уравнений:
{εr=6ε4+r=2)
ε=6r
6r4+r=2
6r=8+2r
4r=8
r=2 (Ом)
ε=6·2=12 (В)
Теперь можем вычислить искомое сопротивление:
R=12√28−2=4 (Ом)
Ответ: 4pазбирался: Алиса Никитина | обсудить разбор
Задание EF18453
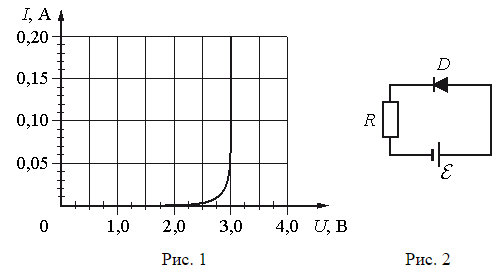
На рис. 1 изображена зависимость силы тока через светодиод D от приложенного к нему напряжения, а на рис. 2 – схема его включения. Напряжение на светодиоде практически не зависит от силы тока через него в интервале значений 0,05 А<I<0,2 А. Этот светодиод соединён последовательно с резистором R и подключён к источнику с ЭДС E1=6 В. При этом сила тока в цепи равна 0,1 А. Какова сила тока, текущего через светодиод, при замене источника на другой с ЭДС E2=4,5 В? Внутренним сопротивлением источников пренебречь.
Алгоритм решения
Решение
Запишем исходные данные:
Из рисунка 1 следует, что при силе тока, равной I1 = 0,1 А напряжение на светодиоде равно UD = 3 В. По закону Ома для участка цепи напряжение на резисторе, будет равно:
U1=I1R
По закону Ома для полной (замкнутой) цепи, имеем:
ε1=U1+UD
Следовательно:
U1=ε1−UD
Тогда сопротивление резистора равно:
R=ε1−UDI1
Напряжение на светодиоде не зависит от силы тока, проходящего через него в интервале значений (это следует из графика рис. 1), поэтому U2=ε2−UDдля любой силы тока из этого интервала значений, следовательно, сила тока в цепи при изменении ЭДС источника:
I2=U2R=ε2−UDR=I1ε2−UDε1−UD
I2=0,14,5−36−3=0,05 (А)
Ответ: 0,05pазбирался: Алиса Никитина | обсудить разбор
Задание EF17725
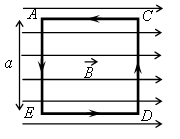 На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Алгоритм решения
Решение
По условию задачи известными данными являются:
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12mga
Отсюда выразим силу тока:
I>mga2a2B
I>mg2aB
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18860
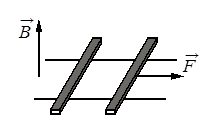 По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
Алгоритм решения
Решение
Запишем исходные данные:
100 г = 0,1 кг
10 см = 0,1 м
Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:
εi=vBlsinα
Причем v — это разность скоростей стержней (v2 – v1), которая характеризует скорость изменения площади проводящего контура.
Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:
εi=IRк
где Rк — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:
Rк=2R
Отсюда закон Ома принимает вид:
εi=2IR
Тогда ток в контуре равен:
I=εi2R=vBlsinα2R
С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):
Fтр=FА
μmg=BIlsinα
Подставим сюда выражение, полученное для силы тока в контуре:
μmg=BvBlsinα2Rlsinα=vB2l2sin2α2R
Отсюда скорость равна:
v=2μmgRB2l2sin2α
Так как синус угла равен «1»:
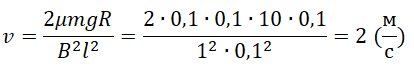
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22800
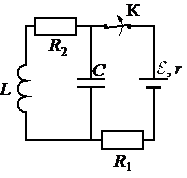 На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС ε = 12 В и внутренним сопротивлением r = 1 Ом, двух резисторов с сопротивлениями R1 = 7 Ом и R2 = 4 Ом, конденсатора электроёмкостью С = 3 мкФ и катушки с индуктивностью L = 32 мкГн. Какое количество теплоты выделится на резисторе R2 после размыкания ключа К? Сопротивлением провода катушки пренебречь. Ответ запишите в мкДж.
На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС ε = 12 В и внутренним сопротивлением r = 1 Ом, двух резисторов с сопротивлениями R1 = 7 Ом и R2 = 4 Ом, конденсатора электроёмкостью С = 3 мкФ и катушки с индуктивностью L = 32 мкГн. Какое количество теплоты выделится на резисторе R2 после размыкания ключа К? Сопротивлением провода катушки пренебречь. Ответ запишите в мкДж.
Решение
Запишем исходные данные:
3 мкФ = 3∙10–6 Ф
32 мкГн = 32∙10–6 Гн
До размыкания ключа электрический ток протекает через последовательно соединённые резисторы R1, R2 и катушку L. После размыкания ключа вся накопленная в элементах цепи энергия выделится в виде тепла на резисторе R2:
E=Wкон+Wкат
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22
Напряжение U на конденсаторе можно выразит из закона Ома для участка цепи:
U=IR2
Чтобы выразить силу тока, потребуется записать закон Ома для полной цепи:
I=εR+r
Так как в цепи есть два последовательно соединенных резистора, общее сопротивление цепи будет равно сумме их сопротивлений:
R=R1+R2
Тогда закон Ома для полной цепи примет вид:
I=εR1+R2+r
Тогда напряжение на конденсаторе равно:
U=εR2R1+R2+r
Следовательно, энергия электрического поля в конденсаторе будет равна:
Wкон=C2(εR2R1+R2+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR1+R2+r)2
Следовательно, на втором резисторе выделится энергия, равная:
E=C2(εR2R1+R2+r)2+L2(εR1+R2+r)2
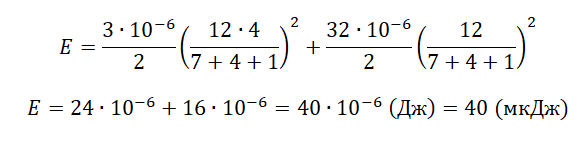
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22801
Период свободных электромагнитных колебаний в идеальном колебательном контуре, состоящем из конденсатора и катушки индуктивности, равен 6,3 мкс. Амплитуда колебаний силы тока Im=5 мА. В момент времени t сила тока в катушке равна 3мА. Найдите заряд конденсатора в этот момент. Ответ округлите до целых и запишите в нКл.
Алгоритм решения
Решение
Запишем исходные данные:
6,3 мкс = 6,3∙10–6 с
5 мА = 5∙10–3 А
3 мА = 3∙10–3 А
Закон сохранения энергии в колебательном контуре имеет вид:
W=Li22+q22C=LI2max2
Запишем формулу Томсона:
T=2π√LC
Выразим из закона сохранения энергии заряд конденсатора:
q2=2С(LI2max2−Li22)=CL(I2max−i2)
q=√CL(I2max−i2)
Выразим емкость конденсатора из формулы Томсона:
√LC=T2π
C=1L(T2π)2
q=⎷1L(T2π)2L(I2max−i2)=T2π√I2max−i2
4·10−9 (Кл)=4 (нКл)
Ответ: 4pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
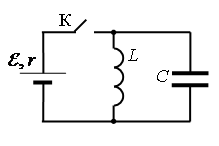 В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
Алгоритм решения
Решение
Запишем исходные данные:
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85pазбирался: Алиса Никитина | обсудить разбор
Задание EF19015
На дне бассейна с водой находится небольшая лампочка. На поверхности воды плавает круглый плот – так, что центр плота находится точно над лампочкой. Определите глубину бассейна Н, если минимальный радиус плота, при котором свет от лампочки не выходит из воды, R = 2,4 м. Сделайте рисунок, поясняющий решение. Толщиной плота пренебречь. Показатель преломления воды n = 4/3.
Алгоритм решения
Решение
Запишем исходные данные:
Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.
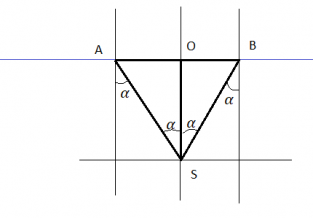
Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:
sinα=1n
Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.
Пусть α — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.
Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:
H=Rcotα
Котангенс угла определяется как отношение косинуса этого угла к его синусу:
cotα=cosαsinα
Косинус угла можем выразить из основного тригонометрического тождества:
sin2α+cos2α=1
Следовательно:
cosα=√1−sin2α
Отсюда котангенс равен:
cotα=√1−sin2αsinα
Тогда глубина бассейна:
H=Rcotα=R√1−sin2αsinα
Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:
H=R√1−(1n)21n=Rn√1−1n2
Подставим известные данные и получим:
H=2,4·43⎷1−1(43)2=3,2√1−916=3,2√74≈0,8·2,65=2,12 ⎛⎜⎜⎝м⎞⎟⎟⎠
Ответ: 2,12
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17760
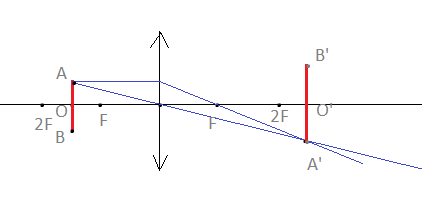
 Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Алгоритм решения
Решение
Запишем исходные данные:
4 см = 0,04 м
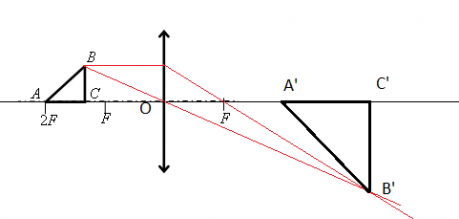
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19112
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе. Ответ запишите в м/с.
Алгоритм решения
Решение
Запишем исходные данные:
10 см = 0,1 м
15 см = 0,15 м
Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.
Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.
Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:
Γ=Rr
Линейное увеличение также определяется формулой:
Γ=fd
Следовательно:
Rr=fd
Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:
Rr=dFd(d−F)=Fd−F
Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:
ω=vr=VR
Отсюда линейная скорость движения изображения равна:
V=Rvr=Fvd−F=0,1·50,15−0,1=10 (мс)
Ответ: 10pазбирался: Алиса Никитина | обсудить разбор
👀 4.3k