Задание №26 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Для решения задания № 26 необходимо понимание сути процессов, происходящих в идеальных газах при тех или иных условиях. Кроме того, может потребоваться использование понятий и применение формул, относящихся к курсу молекулярно-кинетической теории.
Задание ЕГЭ-Ф-ДВ2023-26
Алгоритм решения:
Решение:
Запишем исходные данные:
Формула тонкой линзы:
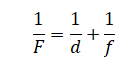
Или:
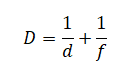
Линейное увеличение также может быть определено следующими формулами:
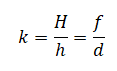
d — расстояние межу предметом и линзой, f — расстояние между линзой и изображением предмета. Следовательно, нам нужно найти значение f + d — расстояние от предмета до его изображения.
Выразим из второй формулы расстояние между линзой и изображением предмета:
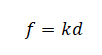
Подставим это выражение в формулу тонкой линзы и получим:
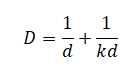
Теперь выразим отсюда расстояние межу предметом и линзой:
.
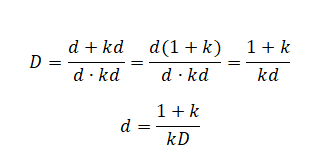
Теперь выразим таким же способом из второй формулы расстояние межу предметом и линзой, чтобы найти формулу для определения расстояния между линзой и изображением предмета через формулу тонкой линзы:
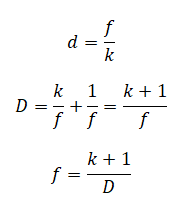
Отсюда расстояние между предметом и его изображением равно:
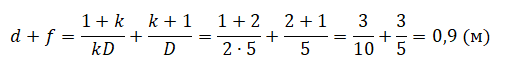
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17985
За время t=4 с детектор поглощает N=6⋅105 фотонов падающего на него монохроматического света. Поглощаемая мощность P=5⋅10−14 Вт. Какова длина волны падающего света?
Ответ:
а) 0,4 мкм
б) 0,6 мкм
в) 520 нм
г) 780 нм
Алгоритм решения
Решение
Запишем исходные данные:
Вся энергия фотонов будет поглощена детектором. Согласно закону сохранения энергии:
Nhν=Pt
Длина волны определяется формулой:
λ=cν
Отсюда частота равна:
ν=cλ
Подставим это выражение в записанный закон сохранения энергии:
Nhcλ=Pt
Отсюда длина волны равна:
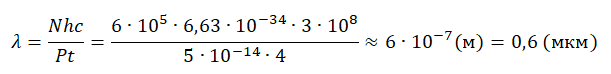
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17650
В сосуде находится разреженный атомарный водород. Атом водорода в основном состоянии (Е1 = – 13,6 эВ) поглощает фотон частотой 3,7⋅1015 Гц. С какой скоростью υ движется вдали от ядра электрон, вылетевший из атома в результате ионизации? Энергией теплового движения атомов водорода пренебречь.
Ответ:
а) 80 км/с
б) 380 км/с
в) 760 км/с
г) 1530 км/с
Алгоритм решения
Решение
Запишем исходные данные:
Запишем второй постулат Бора в математической форме:
hνkn=Ek−En
Скорость электрона мы можем посчитать, если примем энергию электрона в возбужденном состоянии за его кинетическую энергию. Тогда формула примет вид:
hνkn=mv22−En
Сделаем несколько преобразований, чтобы выразить скорость электрона:
mv22=hνkn+En
v2=2(hνkn+En)m
v=√2(hνkn+En)m
Учтем, что:
Тогда:

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17545
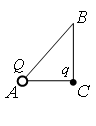 В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
а) 0,36
б) 0,60
в) 0,75
г) 1,67
Алгоритм решения
Решение
Запишем исходные данные:
Запишем закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона для 1 и 2 случая:
FKC=k|q||Q|AC2
FKB=k|q||Q|AB2
По условию задачи нужно найти соотношение сторон треугольника АС к ВC. Для этого выразим известные стороны треугольника из формул выше:
AC=√k|q||Q|FKC
AB=√k|q||Q|FKB
Сторону ВС можно выразить с помощью теоремы Пифагора (АВС — прямоугольный треугольник, так как угол С является прямым):
BC=√AB2−AC2=√k|q||Q|FKB−k|q||Q|FKC=√k|q||Q|(FKC−FKB)FKBFKC
Отсюда:
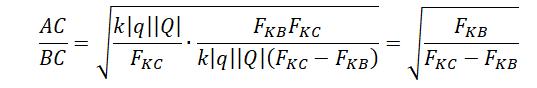
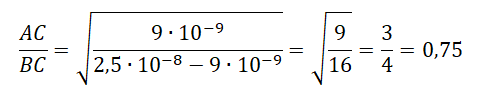
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17616
Пылинка, имеющая массу 10−6 кг, влетела в однородное электрическое поле в направлении против его силовых линий с начальной скоростью 0,3 м/с и переместилась на расстояние 4 см. Каков заряд пылинки, если её скорость уменьшилась при этом на 0,2 м/с, а напряжённость поля 105 В/м?
Ответ:
а) 2 пКл
б) 4 пКл
в) 10 пКл
г) 15 пКл
Алгоритм решения
Решение
Запишем исходные данные:
4 см = 0,04 м
Напряженность электрического поля прямо пропорциональная кулоновской силе, действующей на пробный заряд:
E=FKq0
Так как заряд, влетев в электрическое поле, замедляется, кулоновская сила направлена против вектора его начальной скорости. Это значит, что векторы силы Кулона и напряженности электрического поля совпадают. Следовательно, в поле влетел положительный заряд. Его можно выразить из формулы напряженности:
q0=FKE
Применим второй закон Ньютона:
FK=ma
Ускорение пылинки можно выразить из формулы перемещения при равноускоренном прямолинейном движении без учета времени:
s=v20−v22a=v20−(v0−Δv)22a
a=v20−(v0−Δv)22s
Отсюда кулоновская сила равна:
FK=mv20−(v0−Δv)22s
Заряд равен:
q0=mv20−(v0−Δv)22sE
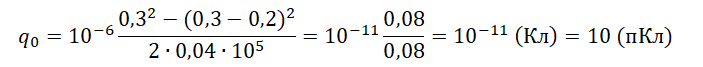
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18357
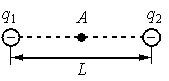 Два точечных отрицательных заряда: q1=−20 нКл и q2=−40 нКл находятся в вакууме на расстоянии L=1,5м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов.
Два точечных отрицательных заряда: q1=−20 нКл и q2=−40 нКл находятся в вакууме на расстоянии L=1,5м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов.
Ответ:
а) 160 Н/Кл
б) 320 Н/Кл
в) 125 Н/Кл
г) 640 Н/Кл
Алгоритм решения
Решение
Запишем исходные данные:
–20 нКл = –20∙10–9 Кл
–40 нКл = –40∙10–9 Кл
Вектор напряженности поля, создаваемого первым зарядом в точке А, направлен влево (в сторону заряда), так как он отрицательный. Второй заряд тоже отрицательный, но он лежит по другую сторону от точки А. Поэтому в ней вектор напряженности поля, создаваемого вторым зарядом, будет направлен вправо. Так как модуль второго заряда больше модуля первого, результирующая напряженность будет направлена вправо. Напряженность в точке А в этом случае будет вычисляться как разность двух напряженности:
EA=E2−E1
Напряженность определяется формулой:
E=k|q|r2
Следовательно:
EA=k|q2|(0,5L)2−k|q1|(0,5L)2=k(0,5L)2(|q2|−|q1|)
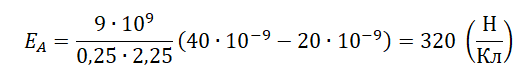
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22543
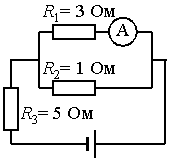 В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.
В цепи, изображённой на рисунке, идеальный амперметр показывает 1 А. Найдите ЭДС источника, если его внутреннее сопротивление 1 Ом.
Ответ:
а) 23 В
б) 25 В
в) 27 В
г) 29 В
Алгоритм решения
Решение
Запишем исходные данные:
Закон Ома для полной цепи:
I=εR+r
R — полное сопротивление внешней цепи. Цепь состоит из последовательно соединенного третьего резистора с параллельным участком цепи, состоящим из первого и второго резисторов. Вычислим сопротивление параллельного участка цепи:
1R12=1R1+1R2
R12=R1R2R1+R2
Полное сопротивление внешней цепи равно:
R=R12+R3=R1R2R1+R2+R3
Следовательно, ЭДС источника тока равен:
ε=I(R+r)=I(R1R2R1+R2+R3+r)
Полная сила тока равна силе тока параллельного участка цепи, так как I = I3 = I12. А сила тока параллельного участка цепи равна сумме силы тока на первом и втором резисторе:
I12=I1+I2=I
Сначала найдем напряжение на первом резисторе, используя закон Ома для участка цепи:
U1=I1R1
Так как это параллельный участок, то:
U1=U2=U12
Следовательно, сила тока на втором резисторе равна:
I2=U2R2=I1R1R2
Сила тока на всем участке цепи равна:
I=I12=I1+I1R1R2=I1(1+R1R2)
Теперь можем вычислить ЭДС источника тока:
ε=I1(1+R1R2)(R1R2R1+R2+R3+r)
ε=1(1+31)(3·13+1+5+1)=6,75·4=27 (В)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF17511
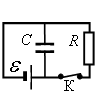 Конденсатор ёмкостью С = 2 мкФ присоединён к батарее с ЭДС ε = 10 В и внутренним сопротивлением r = 1 Ом. В начальный момент времени ключ К был замкнут (см. рисунок). Какой станет энергия конденсатора через длительное время (не менее 1 с) после размыкания ключа К, если сопротивление резистора R = 10 Ом? Ответ округлите до сотен.
Конденсатор ёмкостью С = 2 мкФ присоединён к батарее с ЭДС ε = 10 В и внутренним сопротивлением r = 1 Ом. В начальный момент времени ключ К был замкнут (см. рисунок). Какой станет энергия конденсатора через длительное время (не менее 1 с) после размыкания ключа К, если сопротивление резистора R = 10 Ом? Ответ округлите до сотен.
Ответ:
а) 100 нДж
б) 200 нДж
в) 100 мкДж
г) 200 мкДж
Алгоритм решения
Решение
Запишем исходные данные:
2 мкФ = 2∙10–6 Ф
Запишем закон Ома для полной цепи:
I=εR+r
Энергия конденсатора определяется формулой:
W=CU22
Напряжение внешней цепи связано с ЭЛС источника формулой:
U=ε−Ir
Используя закон Ома для полной цепи, получаем:
U=ε−εrR+r=εR+εr−εrR+r=εRR+r
Тогда энергия конденсатора через длительное время станет равной:
W=12C(εRR+r)2
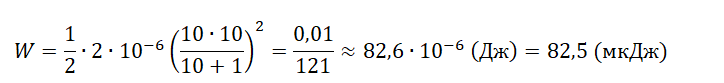
Округлим ответ до сотен и получим 100 мкДж.
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
Решение
Запишем исходные данные:
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsinα
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR
Сопротивление проводника вычисляется по формуле:
R=rlS
Тогда сила тока равна:
I=USrl
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl=BUSr=1·2,4·2·10−20,12=0,4 (Н)
Ответ: 0,4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17754
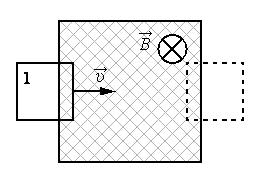 В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
Ответ:
а) 1 мА
б) 5 мА
в) 10 мА
г) 20 мА
Алгоритм решения
Решения
Запишем исходные данные:
10 см = 0,1 м
Индукционный ток, возникающий в рамке, определяется по формуле:
Ii=εiR
Закон электромагнитной индукции для движущихся проводников:
εi=vBlsinα
Отсюда индукционный ток равен:
Ii=vBlsinαR
На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:
Ii=vBlsin90°R=1·0,1·0,1·110=0,001 (А)=1 (мА)
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF22682
Алгоритм решения
Решение
Запишем исходные данные:
Сделаем рисунок. Так как препятствие квадратное, оно располагается параллельно полу, а его центр лежит на одной вертикали с точечным источником света, можем построить рисунок, наблюдая картину с одной стороны квадратного препятствия. В этом случае OE соответствует высоте потолка, EB — расстоянию от пола до препятствия, а AC — стороне квадратного препятствия. При этом тень будет иметь форму квадрата. Поэтому для нахождения ее площади достаточно найти сторону этого квадрата — DF.
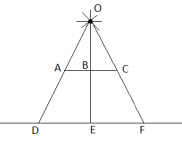
Треугольники OBC и OEF являются подобными по трем углам. Угол O у них общий. Углы B и E — прямые (так как они образованы при пересечении вертикалью двух параллельных плоскостей). А углы C и F равны как углы при параллельных прямых и секущей.
Следовательно, OB относится к OE так же, как BC относится к EF. Причем EF — половина стороны квадрата тени, поскольку треугольник DOF — равнобедренный. Это следует из того, что перпендикуляр, проведенный к основанию равнобедренного треугольника, одновременно является его биссектрисой и медианой. Следовательно, отрезок OE делит на 2 равные части DF.
Отсюда:
OBOE=BCEF
Умножим числитель и знаменатель дроби в правой части уравнения и получим:
OBOE=2BC2EF=ACDF
Причем OB можно вычислить как разность высоты потолка и расстояния от препятствия до пола:
OB=OE−BE
Получаем:
DF=OE·ACH−h=aHH−h=2·44−2=4 (м)
Это сторона квадрата тени. Чтобы найти площадь тени, нужно возвести эту величину в квадрат:
S=DF2=42=16 (м2)
Ответ: 16pазбирался: Алиса Никитина | обсудить разбор
Задание EF17685
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Ответ:
а) 0,50 м
б) 0,75 м
в) 1,25 м
г) 1,50 м
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Алгоритм решения
Решение
Запишем известные данные:
Запишем формулу увеличения линзы и выразим из нее расстояние от линзы до изображения предмета:
Γ=fd
f=Γd
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Γd=dFd−F
Поделим на d и выразим расстояние от предмета до линзы:
Γ=Fd−F
d=FΓ+F=14+1=1,25 (м)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF18124
Предмет высотой 6 см расположен на горизонтальной главной оптической оси тонкой собирающей линзы на расстоянии 30 см от её оптического центра. Высота изображения предмета 12 см. Найдите фокусное расстояние линзы.
Ответ:
а) 5 см
б) 10 см
в) 20 см
г) 36 см
Алгоритм решения
Решение
Запишем известные данные:
Так как все данные измеряются в сантиметрах, переводить единицы измерения величин в СИ нет необходимости. Просто ответ будет получен тоже в сантиметрах.
Запишем формулу увеличения линзы:
Γ=Hh=fd
Отсюда расстояние от изображения до линзы равно:
f=Hdh
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Hdh=dFd−F
Поделим на d, у множим на h(d –F) и выразим фокусное расстояние:
Hh=Fd−F
H(d−F)=hF
Hd−HF=hF
hF+HF=Hd
F(h+H)=Hd
F=Hdh+H=12·3012+6=20 (см)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF18230
Дифракционная решётка с периодом 10–5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.
Алгоритм решения
Решение
Запишем исходные данные:
0,4 мкм = 0,4∙10–6 м.
3 см = 3∙10–2 м
Сделаем пояснительный чертеж:
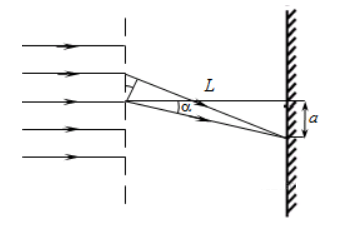
Запишем условие интерференционных максимумов дифракционной решётки:
dsinα=kλ
Из курса геометрии известно, что тангенс угла равен отношению прилежащего катета к противолежащему. Следовательно:
tanα=aL
Из условия задачи синус и тангенс этого угла равны. Следовательно:
sinα=tanα=aL
Найдём номер дифракционного максимума, который будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины:
daL=kλ
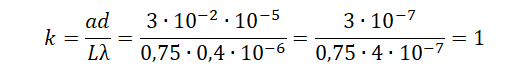
pазбирался: Алиса Никитина | обсудить разбор
👀 4.2k