Задание №4 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
В четвертом задании ЕГЭ по физике у нас проверяют знания сообщающихся сосудов, силы Архимеда, закона Паскаля, моментов сил.
Задание ЕГЭ-Ф-ДВ2023-2
Алгоритм решения:
- Записать исходные данные.
- Записать второй закон Ньютона.
- Применить второй закон Ньютона для случаев 1 и 2.
- Получить формулу для определения искомой величины (силы, которая действует на тело 2).
- Подставить известные данные и произвести вычисления.
Решение:
Запишем исходные данные:
- Сила, которая действует на тело массой m и сообщает ему ускорение a: F = 16 Н.
- Масса второго тела: m2 = m/2.
- Ускорение второго тела: a2 = a/4.
Запишем второй закон Ньютона:
![]()
Применим закон к случаям 1 и 2:
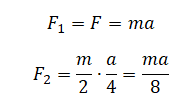
Так как произведение массы на ускорение равно силе, действующей на тело 1, можем выразить силу, действующую на тело 2 следующим образом:
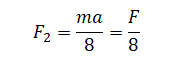
Подставляем известные данные:
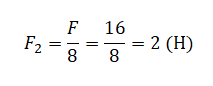
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22660
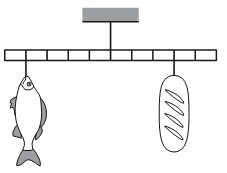 Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.
Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.Алгоритм решения
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18706
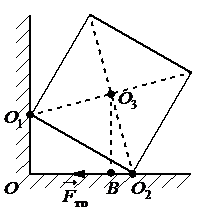 Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно...
Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно...
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: гpазбирался: Алиса Никитина | обсудить разбор
Задание EF18645
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22709
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16pазбирался: Алиса Никитина | обсудить разбор
Задание EF18172
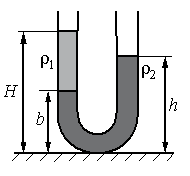 В широкую U-образную трубку, расположенную вертикально, налиты жидкости плотностью ρ1 и ρ2 (см. рисунок). Жидкости не смешиваются. На рисунке b = 15 см, h = 30 см, H = 35 см. Отношение плотности ρ1 к плотности ρ2 равно …
В широкую U-образную трубку, расположенную вертикально, налиты жидкости плотностью ρ1 и ρ2 (см. рисунок). Жидкости не смешиваются. На рисунке b = 15 см, h = 30 см, H = 35 см. Отношение плотности ρ1 к плотности ρ2 равно …
Ответ:
а) 0,67
б) 0,75
в) 0,86
г) 1,33
Алгоритм решения
Решение
Запишем исходные данные:
Внимание! В данном случае переводить единицы в СИ необязательно, так как на величину отношения они никак не повлияют.
Запишем условие равновесия. Давление на уровне b в обоих коленах должно быть одинаковое. Поэтому:
ρ1g(H – b) = ρ2g(h – b)
Отсюда:
ρ1ρ2=g(h−b)g(H−b)=h−bH−b=30−1535−15=1520=0,75
Ответ: бpазбирался: Алиса Никитина | обсудить разбор
Задание EF19116
Какова глубина вертикальной шахты, если звук выстрела, произведённого у входа в шахту на поверхности земли, вернулся к стрелку, отразившись от дна шахты, через 0,5с после выстрела? Скорость звука в воздухе считать равной 340 м/с.
Алгоритм решения
Решение
Запишем исходные данные:
Звук от выстрела проделает путь, равный двойному расстоянию от стрелка до дна шахты. Сначала он достигнет дна шахты, затем вернется к стрелку. Поскольку скорость звука постоянна, для преодоления половины пути потребуется вдвое меньше времени. Следовательно, для нахождения времени между выстрелом и эхо нужно умножить скорость звука в воздухе на половину промежутка времени между выстрелом и эхом:
s=vt2=340·0,52=85 (м)
Ответ: 85pазбирался: Алиса Никитина | обсудить разбор
Задание EF22741
Колеблющаяся струна издаёт звук с длиной волны 0,68 м. Какова частота её колебаний, если скорость звука в воздухе 340 м/с?
Алгоритм решения
Решение
Запишем исходные данные:
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν
Отсюда:
ν=vλ=3400,68=500 (Гц)
Ответ: 500pазбирался: Алиса Никитина | обсудить разбор
Задание EF18242
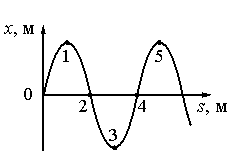 На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна
На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна
Ответ:
а) π/3
б) π/2
в) π
г) 2π
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Ответ: гpазбирался: Алиса Никитина | обсудить разбор
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения
Решение
Запишем исходные данные:
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν=4·400=1600 (мс)
Ответ: 1600pазбирался: Алиса Никитина | обсудить разбор
Задание EF18803
На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с.
Алгоритм решения
Решение
Запишем исходные данные:
Звук от удара проделает путь, равный одинарному расстоянию от наблюдателя до источника звука. Следовательно, для нахождения времени, через которое наблюдатель услышит звук, нужно разделить этот путь на скорость звука в воздухе:
t=sv=510340=1,5 (с)
Ответ: 1,5pазбирался: Алиса Никитина | обсудить разбор
Задание EF17593
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.

Каков период колебаний шарика?
Ответ:
а) 1 с
б) 2 с
в) 3,2 с
г) 4 сАлгоритм решения
Решение
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T=2(t2−t1)=2(3−1)=4 (с)
Ответ: гpазбирался: Алиса Никитина | обсудить разбор
Задание EF18740
Через какое время после выстрела придёт к охотнику эхо от звука выстрела, если расстояние до преграды, от которой отразится звук, равно 850 м? Скорость звука в воздухе считать равной 340 м/с.
Алгоритм решения
Решение
Запишем исходные данные:
- Скорость распространения звука в воздухе: v = 340 м/с.
- Расстояние до преграды: s = 850 м.
Звук от выстрела проделает путь, равный двойному расстоянию от охотника до преграды. Сначала он достигнет преграды, затем вернется к охотнику. Следовательно, для нахождения времени между выстрелом и эхо нужно разделить этот путь на скорость звука в воздухе:
t=2sv=2·850340=5 (с)
Ответ: 5pазбирался: Алиса Никитина | обсудить разбор
👀 11.1k