Задание №6 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
В задании №6 ЕГЭ по физике необходимо выбрать правильное заключение, проанализировав условие задачи. Тематика задач - механика.
Задание ЕГЭ-Ф-ДВ2023-4
Небольшой груз, покоящийся на гладком горизонтальном столе, соединён пружиной со стенкой. Груз немного смещают от положения равновесия вдоль оси пружины и отпускают из состояния покоя, после чего он начинает колебаться, двигаясь вдоль оси пружины, параллельно которой направлена ось Ox. В таблице приведены значения координаты груза х в различные моменты времени t. Выберите все верные утверждения о результатах этого опыта на основании данных, содержащихся в таблице. Абсолютная погрешность измерения координаты равна 0,1 см, времени – 0,05 с.

1) В момент времени 1,50 с ускорение груза максимально. 2) В момент времени 0,50 с кинетическая энергия груза максимальна. 3) Модуль силы, с которой пружина действует на груз, в момент времени 1,00 с меньше, чем в момент времени 0,25 с. 4) Период колебаний груза равен 1 с. 5) Частота колебаний груза равна 0,5 Гц.
Алгоритм решения:
- Проверить истинность утверждения 1. Для этого необходимо установить зависимость ускорения тела, колеблющегося на пружине, от его координаты.
- Проверить истинность утверждения 2. Для этого необходимо установить зависимость кинетической энергии тела, колеблющегося на пружине, от его координаты.
- Проверить истинность утверждения 3. Для этого необходимо записать формулу, отображающую зависимость между силой, действующей на колеблющееся тело, и координатой этого тела. Затем найти модули силы для указанных значений времени и сравнить их.
- Проверить истинность утверждения 4. Для этого необходимо дать определение периоду колебаний, установить период колебаний тела и сравнить его со значением, приведенным в утверждении 4.
- Проверить истинность утверждения 5. Для этого необходимо дать определение частоте колебаний, установить частоту колебаний тела и сравнить его со значением, приведенным в утверждении 5.
- Записать ответ в виде последовательности цифр, не разделенных знаками препинания и пробелами.
Решение:
Проверяем истинность утверждения 1, согласно которому в момент времени 1,50 с ускорение груза максимально. Ускорение груза, колеблющегося на горизонтальной пружине, можно выразить из 2 закона Ньютона (учитываем, что на тело действует сила упругости):
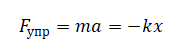
Отсюда ускорение равно:
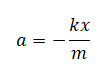
Отношение жесткости пружины к массе груза постоянно, так как эти величины не изменяются. Следовательно, ускорение пропорционально координате колеблющегося тела. И если в момент времени 1,50 с координата тела (отклонение от положения равновесия) максимальна, то ускорение тоже максимально. Однако в соответствии с данными таблицы, в этот момент времени координата тела равна 0,0 см. Следовательно, утверждение 1 неверно.
Проверяем истинность утверждения 2, согласно которому в момент времени 0,50 с кинетическая энергия груза максимальна. Полная механическая энергия тела равна сумме его потенциальной и кинетической энергий:
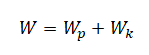
Когда кинетическая энергия груза максимальна, потенциальная энергия равна 0. А потенциальная энергия тела, колеблющегося на пружине, определяется формулой:
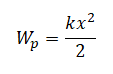
Потенциальная энергия будет равна 0 только в том случае, если в данный момент времени координата тела равна 0 (оно находится в положении равновесия). Следовательно, кинетическая энергия груза в момент времени 0,50 с будет максимальна, если координата тела в это время равна 0. В соответствии с данными таблицы, это действительно так. Следовательно, утверждение 2 верно.
Проверяем истинность утверждения 3, согласно которому модуль силы, с которой пружина действует на груз, в момент времени 1,00 с меньше, чем в момент времени 0,25 с.
Запишем закон Гука:
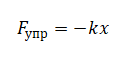
В момент времени 1,00 с координата груза равна –3 см. Так как в данных вычислениях нам нужно лишь сравнить 2 модуля силы, не будем переводить единицы измерения в СИ — для сравнения достаточно, чтобы единицы изменения были одинаковыми. Следовательно, модуль силы упругости в момент времени 1,00 равен:
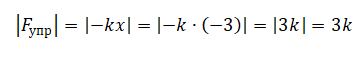
В момент времени 0,25 с координата груза равна 2,1 см. Следовательно, сила упругости равна:
![]()
Видно, 3k больше 2,1k. Следовательно, утверждение 3 неверно.
Проверим истинность утверждения 4, согласно которому период колебаний груза равен 1 с. Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с). Одно полное колебание груз совершает, когда оно возвращается в прежнее положение, пройдя все 4 фазы колебания. Следовательно, если груз начал движение, имея координату 3,0, равную максимальному отклонению от положения равновесия, то периодом будет время, которое ему потребуется для того, чтобы преодолеть положение равновесия, отклониться на максимальное расстояние в обратном положении и вернуться в исходное положение, проходя через точку равновесия.
По таблице видно, что половину колебательного движения груз совершил в момент времени 1,00 с, когда он отклонился на максимальное расстояние в противоположную сторону. Следовательно, столько же времени потребуется грузу, чтобы вернуться в исходное положение. Всего время 1 полного колебания, или период колебаний, составит 2 с. Следовательно, утверждение 4 неверно.
Проверим истинность утверждения 4, согласно которому частота колебаний груза равна 0,5 Гц. Частота — количество колебаний, совершенных в единицу времени. Обозначается как ν («ню»). Единица измерения — 1/секунда, или секунда–1, или герц (1/с, или с–1, или Гц). Частота равна обратной величине периода колебаний:
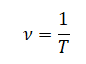
Выше мы выяснили, что период равен 2 с. Следовательно, частота колебаний равна:
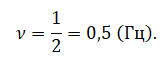
Следовательно, утверждение 5 верно.
Записываем ответ: 25.
Ответ: 25pазбирался: Алиса Никитина | обсудить разбор
Задание E17590
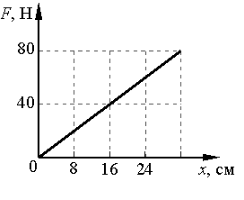 На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?
На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?
а) 250 Н/м
б) 160 Н/м
в) 2,5 Н/м
г) 1,6 Н/м
Алгоритм решения
Решение
Запишем закон Гука:
Fупр = kx
Отсюда коэффициент упругости пружины равен:
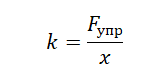
Возьмем на графике точку, соответствующую удлинению пружины 16 см. Ей соответствует модуль силы упругости, равный 40 Н. Переведем сантиметры в метры: 16 см = 0,16 м.
Вычислим жесткость пружины:
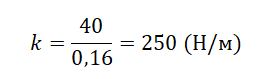
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18521
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
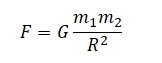
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18133
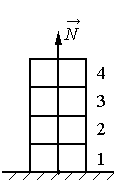 Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…
Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…
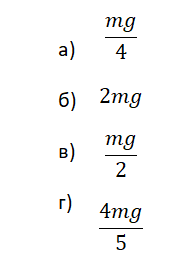
Алгоритм решения
Решение
Так как кирпичи покоятся, вес каждого равен:
P = mg
Вес двух кирпичей равен:
2P = 2mg
Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.
Следовательно:
N = 2P = 2mg
Ответ: бpазбирался: Алиса Никитина | обсудить разбор
Задание EF17993
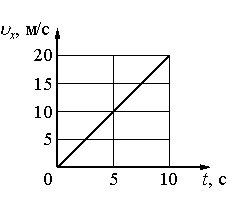 Скорость тела массой 5 кг, движущегося вдоль оси Ох в инерциальной системе отсчёта, изменяется со временем в соответствии с графиком (см. рисунок). Равнодействующая приложенных к телу сил в момент времени t=2,5 с равна…
Скорость тела массой 5 кг, движущегося вдоль оси Ох в инерциальной системе отсчёта, изменяется со временем в соответствии с графиком (см. рисунок). Равнодействующая приложенных к телу сил в момент времени t=2,5 с равна…
а) 2Н
б) 8 Н
в) 10 Н
г) 20 Н
Алгоритм решения
Решение
Запишем исходные данные:
Так как графиком скорости является прямая, непараллельная ось времени, тело движется с постоянным ускорением. Если ускорение постоянно, равнодействующая сил тоже будет постоянной в любой момент времени. Поэтому нам достаточно использовать координаты любой, более удобной для их определения точки. К примеру, в точке, соответствующей моменту времени 10 с.
Запишем второй закон Ньютона:
F = ma
Ускорение тела определяется как отношение изменения скорости ко времени, в течение которого эта скорость менялась. Согласно графику, за 10 секунд скорость изменилась на 20 м/с. Следовательно, ускорение равно:
a = 20/10 = 2 (м/с2)
Теперь можем вычислить равнодействующую сил:
F = ma = 5∙2 = 10 (Н)
Ответ: вpазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
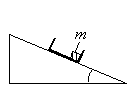 С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
|
|
|
|
Алгоритм решения
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится 2) уменьшится 3) не изменитсяЗапишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
![]()
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:
![]()
Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
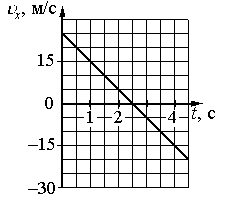
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
👀 9.6k