Задание №9 ОГЭ по математике

Имеем линейное уравнение:

2 + 3х= – 7х – 5

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

2 + 3х= – 7х – 5

3х + 7х= – 5 – 2

10х= –7

х=–7:10

х=–0,7

Найдите корень уравнения:

Обе части уравнения приводим к единому знаменателю 12:

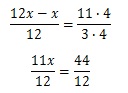
Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:

11х=44

х=44:11

х=4

Найдите корень уравнения:

режде всего, исключим корень, который не входит в ОДЗ:

x+6≠0  → х≠–6

Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:

Применим правило пропорции. Перемножим между собой крайние ее члены и средние:

1·1=(х+6)·2

Выполним умножение в левой части уравнения и раскроем скобки справа:

1=2х+12

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

2х+12=1

Переносим 12 из левой части в правую:

2х=1–12

2х=–11

Находим корень:

х=–11/2=–5,5

ОДЗ это значение не исключает, поэтому оно является искомым результатом.

Решите уравнение:

7х - 9 = 40

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой — всё, что известно переносим в правую часть, всё, что неизвестно — оставляем в левой. Далее выполняем необходимое арифметическое действие.

Решение:

7х — 9 = 40

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

7х = 49

х в нашем случае — это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

х = 49/7, откуда

х = 7

Решите уравнение:

8 x² — 10x + 2 = 0

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

4 x² — 5x + 1 = 0

Далее вычисляем дискриминант:

D = b² — 4ac

D = 5² — 4 •4•1 = 9

Вычисляем корни:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

Решите уравнение:

3 x² + 12 x = 0

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

x ( 3 x + 12 ) = 0

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

x = 0

или

3 x + 12 = 0

3 x = -12

x = -4

Так как в ответе просят указать наименьший корень, то это -4.

Найдите корень уравнения:

10 ( x - 9 ) = 7

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x — 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

10x = 7 + 90

10x = 97

Затем делим обе части на 10:

x = 9,7