Задание №18 ОГЭ по математике

задачи на квадратной решетке
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 3 мин.
➕

В 18 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания.

Задание 18OM21R

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

Ответ: 4

pазбирался: Базанов Даниил | обсудить разбор

Задание OM1906o

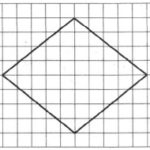
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
Площадь ромба будем искать через его диагонали:

S=d1·d2/2

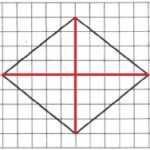
Линии диагоналей обозначим на рисунке красным: Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:

d1=8; d2=10.

Находим площадь фигуры:

S=8·10/2=40

Ответ: 40

pазбирался: Базанов Даниил | обсудить разбор

Задание OM1905o

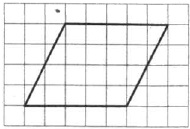
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Площадь параллелограмма вычисляется так:

S=a·ha

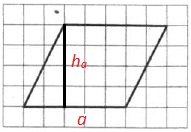
Обозначим a и ha на рисунке: Теперь определим их длины по рисунку:

a=5; ha=4.

Вычисляем искомую площадь:

S=5·4=20.

Ответ: 20

pазбирался: Базанов Даниил | обсудить разбор

Задание OM1904o

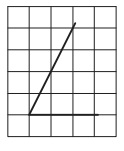
Найдите тангенс острого угла, изображённого на рисунке.
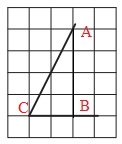
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС: Чтобы получить ответ на вопрос задачи, требуется найти tg∠C. Согласно определению тангенса,  из треугольника ∆АВС можем записать:

tg∠C=AB/BC.

По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):

АВ=4, ВС=2.

Получаем:

tg∠C=4/2=2.

Ответ: 2

pазбирался: Базанов Даниил | обсудить разбор

Задание OM1903o

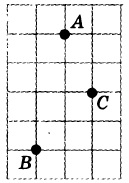
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.решение 12 задания огэ по математике

Проведем необходимые отрезки:

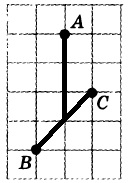
решение 12 задания огэ по математике

Из рисунка можно вычислить длину — это 3.

Ответ: 3

pазбирался: Базанов Даниил | обсудить разбор

Задание OM1902o

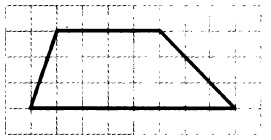
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.решение 12 задания огэ по математике

Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее — 4 клеткам. Полусумма оснований:

( 8 + 4 ) / 2 = 6

Ответ: 6

pазбирался: Базанов Даниил | обсудить разбор

Задание OM1901o

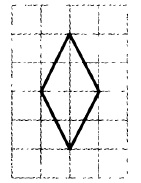
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.решение 12 задания огэ по математике

Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4. Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.

Ответ: 4

pазбирался: Базанов Даниил | обсудить разбор

👀 28.2k