Задание №16 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 2 мин.
В 16 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.
Теория к заданию №16
Несмотря на то, что в задании №16 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».
Начнем рассмотрение с понятия вписанная окружность:
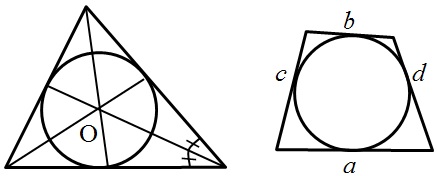
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
- Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d
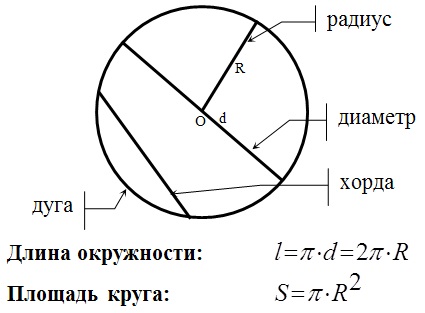
Длинна окружности и площадь:
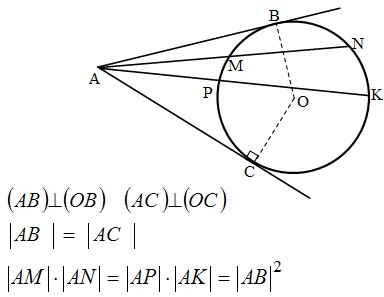
Касательная и секущая:
- Касательная – прямая, имеющая с окружностью одну общую точку.
- Секущая – прямая, имеющая с окружностью две общие точки.
Описанная окружность и её свойства:
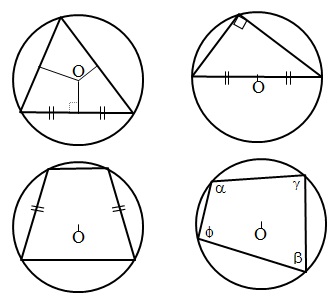
- Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
- Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
- Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
- Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.
Хорда – отрезок, соединяющий две точки окружности.
- Диаметр, делящий хорду пополам, перпендикулярен хорде.
- В окружности равные хорды равноудалены от центра окружности.
- Отрезки пересекающихся хорд связаны равенством:
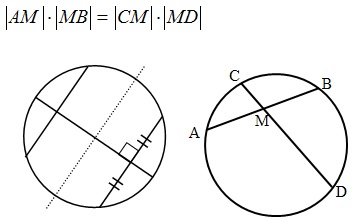
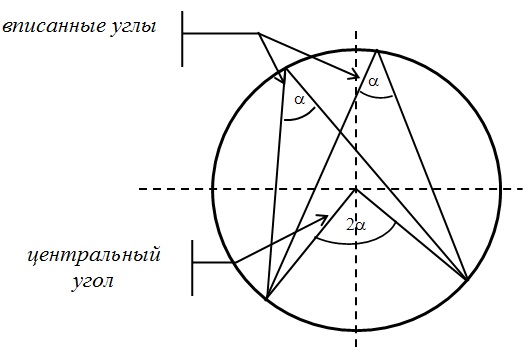
Центральный и вписанный углы:
Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.
Задание 16OM21R
Радиус вписанной в квадрат окружности равен 22√2. Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22√2, то сторона квадрата будет в два раза больше, т.е. 44√2.
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44√2. Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а√2, где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44√2×√2=44√4=44×2=88
Ответ: 88pазбирался: Базанов Даниил | обсудить разбор
Задание OM1706o
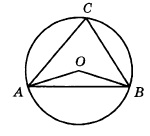
Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=1130.
Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=1130, то угол АСВ равен
0,5 · ᴗАВ = 0,5 · 1130 = 56,50.
Ответ: 56,5pазбирался: Базанов Даниил | обсудить разбор
Задание OM1705o
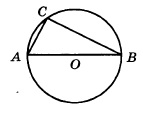
Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 900, и, следовательно, ∆АСВ прямоугольный.
Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора
АС2+ВС2=АВ2 (1)
По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20.
Тогда из (1) получим:
![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1704o
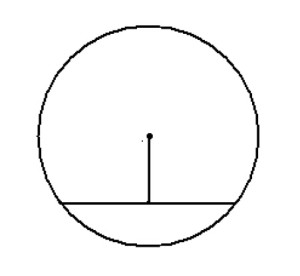
Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:
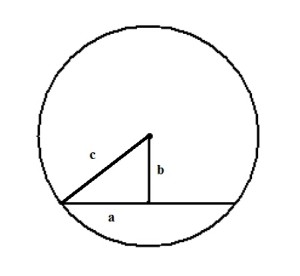
Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a:
a² + b² = c²
a² = c² — b² = 13² — 5² = 169 — 25 = 144
Откуда
а = √144 = 12
Но а — лишь половина хорды, поэтому вся хорда равна 2 • а = 24
Ответ: 24pазбирался: Базанов Даниил | обсудить разбор
Задание OM1703o
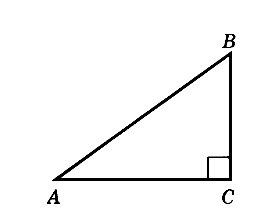
Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.
По теореме Пифагора найдем гипотенузу AB:
AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400
AB = √400 = 20
Гипотенуза равна 20, значит радиус — 10.
Ответ: 10pазбирался: Базанов Даниил | обсудить разбор
Задание OM1702o
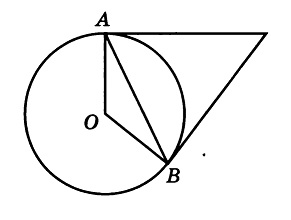
Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:
(180 — 2) / 2 = 89°
Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.
Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:
90 — 89 = 1°
Ответ: 1pазбирался: Базанов Даниил | обсудить разбор
Задание OM1701o
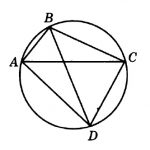
Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:
∠ABD = 92 — 60 = 32
Ответ: 32pазбирался: Базанов Даниил | обсудить разбор
👀 38.4k
Класс.
Классный сайт жаль что я нашел его поздно…)
Добавь сюда пожалуйста еще тему с многоугольниками и с использованием формулы: 180°(n-2)/2
Большое спасибо, уважаемый Даниил Романович! Пользуюсь вашими разработками для подготовки к занятиям.
спасибо за этот сайт