Задание №22 ОГЭ по математике
Первичный бал: 2 Сложность (от 1 до 3): 3 Среднее время выполнения: 15 мин.
В данном задании анализируем функции и их графики.
Задание 22OM21R
у=х2 - |2x +1|
Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки.Раскроем модуль:
{у=х2−2х−1, при х≥−12у=х2+2х+1, при х<−12)
Для построения графика найдем вершины каждой параболы:
у=х2 – 2х – 1
х0=−b2a=22=1
у0=12 -2-1=-2
Итак, вершина первой параболы (1; -2)
Возьмем дополнительные точки, где х ≥−12
| х | -0,5 | 0 | 2 | 3 |
| у | 0,25 | -1 | -1 | 2 |
у=х2 + 2х + 1
Аналогично найдем вершину второй параболы: х0=-1, у0=0
Вершина второй параболы (-1;0)
Дополнительные точки при х<−0.5
| х | -2 | -0,5 |
| у | 1 | 0,25 |
Изобразим параболы в системе координат:
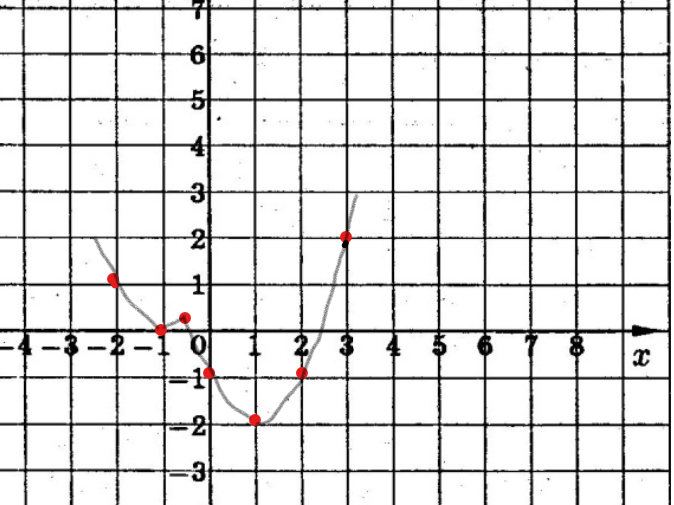
Теперь нам нужно ответить на вопрос задания: «Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки?»
Для этого построим такие прямые (одна желтая, вторая зеленая), откуда видно, что первая прямая совпадает с осью х, т.е. у=0; вторая имеет с графиком три общие точки при у=0,25.
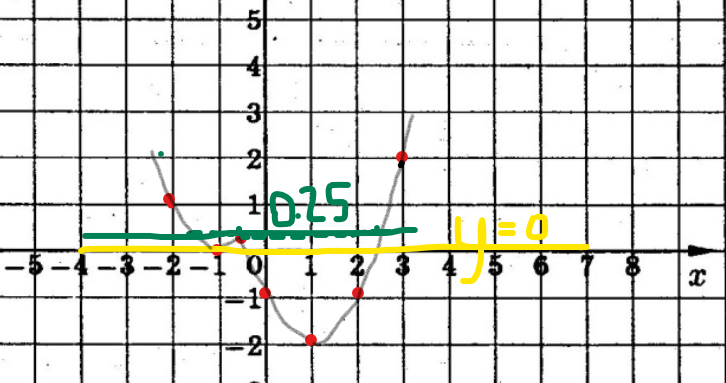
Ответ: при m равных 0; 0,25
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание OM2306o
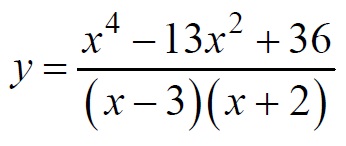
и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку. В ответ запишите наибольшее число.
Разложим числитель дроби на множители:
![]()
При x ≠2 и x ≠ 3 функция принимает вид:
![]()
её график — парабола, из которой выколоты точки ( -2; -4) и ( 3; 6).
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты ( -0,5; -6,25 ). Поэтому c = — 6,25, c = — 4 или c = 6.
Ответ: 6pазбирался: Базанов Даниил | обсудить разбор
Задание OM2305o
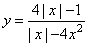
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек. В ответ запишите наибольшее число.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Раскрываем модуль и для каждого случая.
Если x < 0, то
![]()
определена при ![]() и представляет собой часть гиперболы. Дополнительные точки для построения:
и представляет собой часть гиперболы. Дополнительные точки для построения:
| x | -5 | -4 | -3 | -2 | -1 |
| y | -1/5 | -1/4 | -1/3 | -1/2 | -1 |
2. Если x > 0, то
![]()
определена при ![]() и представляет собой часть гиперболы.
и представляет собой часть гиперболы.
Точки для построения графика:
| x | 1 | 2 | 3 | 4 | 5 |
| y | -1 | -1/2 | -1/3 | -1/4 | -1/5 |
3. Изображаем график:
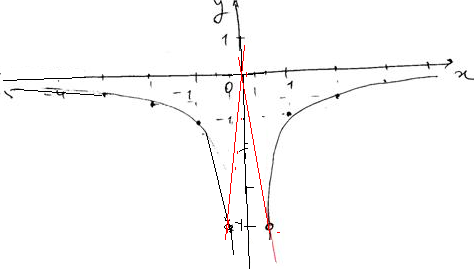
Прямая y=kx не имеет общих точек с графиком данной функции, когда k=-16; 0 и 16. Тогда прямые проходят черед точки с абсциссами ¼ и — ¼ . На рисунке эти прямые изображены красным. При k = 0 прямая совпадает с осью абсцисс. Она тоже не имеет общих точек с графиком.
Ответ: 16pазбирался: Базанов Даниил | обсудить разбор
Задание OM2304o
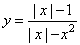
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек. В ответ запишите наибольшее число.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Если x < 0, то
![]()
Дробь, получившаяся в результате, определена ![]() . График представляет собой часть гиперболы.
. График представляет собой часть гиперболы.
Точки для построения графика:
| x | -5 | -4 | -3 | -2 |
| y | -1/5 | -1/4 | -1/3 | -1/2 |
2. Если x > 0, то
![]()
Функция определена при ![]() График представляет собой часть гиперболы.
График представляет собой часть гиперболы.
Точки для построения графика:
| x | 2 | 3 | 4 | 5 |
| y | -1/2 | -1/3 | -1/4 | -1/5 |
3. Построим график заданной функции:
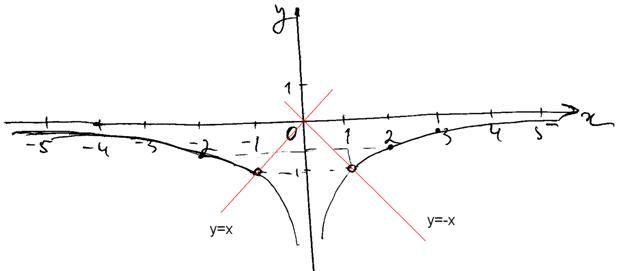
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1 изображены красным. При k = 0 прямая совпадает с осью абсцисс и тоже не имеет общих точек с графиком функции.
Ответ: 1pазбирался: Базанов Даниил | обсудить разбор
Задание OM2303o
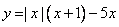
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее число.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
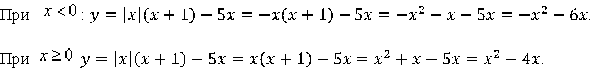
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при ![]() — часть парабола, ветви которой направлены вниз. Потому как коэффициент а=-1 – отрицательный.
— часть парабола, ветви которой направлены вниз. Потому как коэффициент а=-1 – отрицательный.
Определим вершину параболы ![]() и
и ![]() .
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если ![]() , ветви параболы направлены вверх. Найдем вершину:
, ветви параболы направлены вверх. Найдем вершину:
![]() ,
, ![]() (2; -4).
(2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
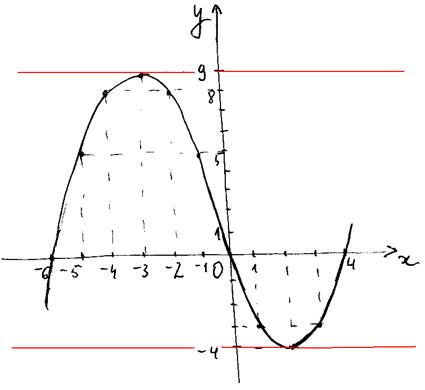
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: 9pазбирался: Базанов Даниил | обсудить разбор
Задание OM2302o
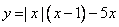
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее из чисел.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
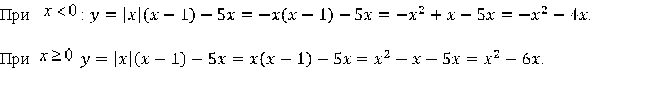
2. Графиком функции ![]() является парабола, ветви которой направлены вниз.
является парабола, ветви которой направлены вниз.
Вершина ее находится в точке : ![]()
![]()
Найдем нули функции: ![]() График проходит через начало координат и точку (0;4).
График проходит через начало координат и точку (0;4).
Графиком второй функции ![]() является парабола, ветви которой направлены вверх.
является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
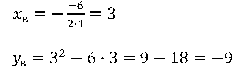
Определим нули параболы ![]()
3. Изображаем график на координатной плоскости:
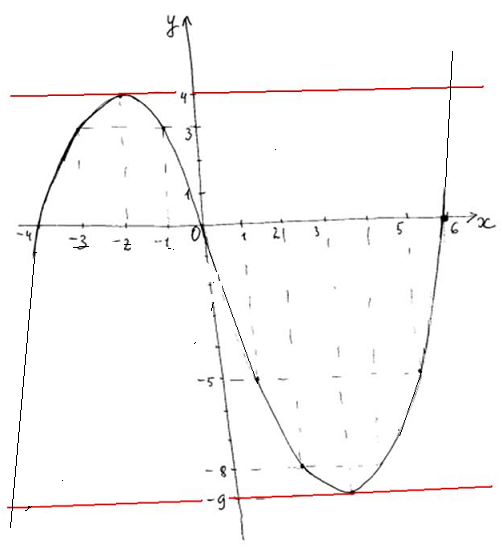
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: 4pазбирался: Базанов Даниил | обсудить разбор
Задание OM2301o
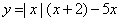
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее число.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
Если ![]() .
. ![]()
Если ![]()
![]()
2. График функции ![]() заданных значениях х — часть параболы, ветви которой направлены вниз.
заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами: ![]()
![]()
Найдем нули функции: ![]() График проходит через начало координат и точку (-2;-7).
График проходит через начало координат и точку (-2;-7).
Графиком второй функции ![]() является парабола, ветви которой направлены вверх.
является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
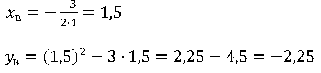
Определим нули параболы ![]()
3. Изображаем график функции на координатной плоскости:
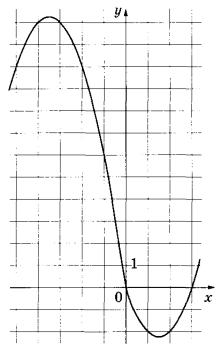
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: 12,25pазбирался: Базанов Даниил | обсудить разбор
👀 33.8k
не поняла,откуда 8 и 4?
Добрый день! Ну как откуда? Собственная скорость — 6, если он плывет по течению, то прибавляется еще скорость течения — 2, итого 8. А если против — то вычитается — тогда 4.
А как решить полученное уравнение ?
откуда в задании 23060 взялись выколотые точки?