Задание №15 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 2 мин.
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей. Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике. Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы. В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №15
Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
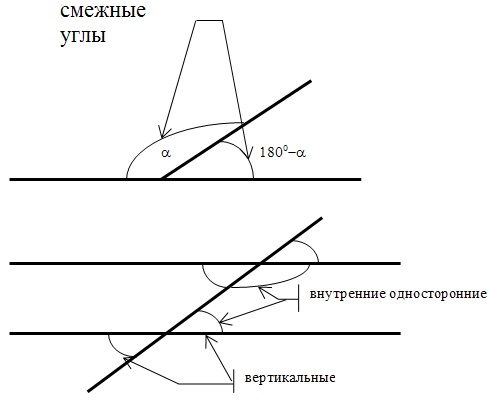
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
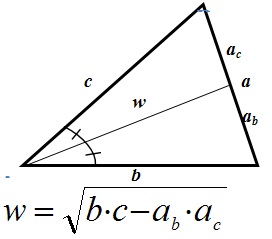
Медиана:
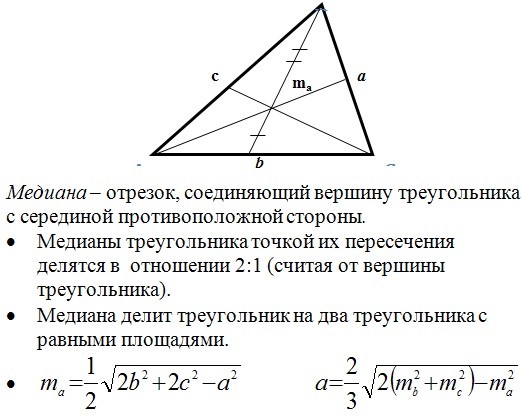
Теперь вспомним основные формулы нахождения площади треугольника:
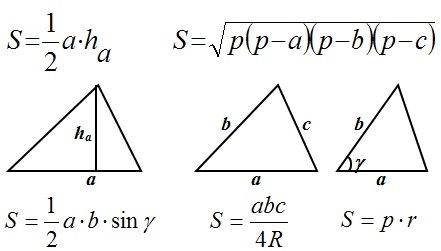
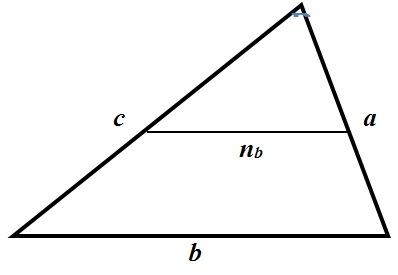
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник — треугольник, у которого две стороны равны.
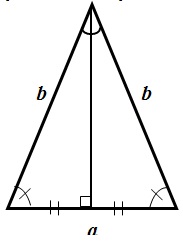
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник — треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
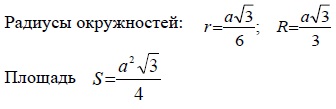
Прямоугольный треугольник:

Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42pазбирался: Базанов Даниил | обсудить разбор
Задание OM1611o
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 — 123 = 57°
Из второго — что ∠BCA = ∠BAC = 57°
Ответ: 57pазбирался: Базанов Даниил | обсудить разбор
Задание OM1610o
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22pазбирался: Базанов Даниил | обсудить разбор
Задание OM1609o
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20pазбирался: Базанов Даниил | обсудить разбор
Задание OM1608o
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18pазбирался: Базанов Даниил | обсудить разбор
Задание OM1607o
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30pазбирался: Базанов Даниил | обсудить разбор
Задание OM1606o
Для решения необходимо вспомнить определение медианы.
Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28pазбирался: Базанов Даниил | обсудить разбор
Задание OM1605o
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 — 23 = 67°
Ответ: 67pазбирался: Базанов Даниил | обсудить разбор
Задание OM1604o
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15pазбирался: Базанов Даниил | обсудить разбор
Задание OM1603o
Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 — 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29pазбирался: Базанов Даниил | обсудить разбор
Задание OM1602o
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия — это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32pазбирался: Базанов Даниил | обсудить разбор
Задание OM1601o
Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 — 73 — 48 = 59
Ответ: 59pазбирался: Базанов Даниил | обсудить разбор
👀 39.7k
А как решать квадратичные системы неравенств?
Находите корни уравнения, рисуете параболу (ветви : вниз, вверх), расставляете знаки, выбираете ответ в зависимости от знака неравенства.
лучший сайт,спасибо
очень помогает