Задание №20 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 3 Среднее время выполнения: 8 мин.
В данном задании необходимо решить уравнение степени больше двух - это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий.
Задание OM2005
Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:
(х−5)2−√7(х−5)<0
Теперь вынесем за скобки общий множитель (х-5), получим:
(х−5)(х−5−√7)<0
Найдем нули функции, приравнивая каждый множитель к нулю:
х−5=0, откуда х=5
х−5−√7=0,
откуда:
х=5+√7
Отметим эти числа на числовом луче и найдем интервал отрицательных чисел:
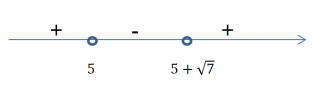
Итак, видно, что необходимый интервал от 5 до (5+√7)
Ответ: (5;5+√7)
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание OM2004
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
(3∙3∙4)n4n−2∙32n−1
Теперь представим каждый множитель в виде степени:
3n∙3n∙4n4n−2∙32n−1
Разложим знаменатель дроби на множители по свойству степеней
3n∙3n∙4n4n∙4−2∙32n∙3−1
Теперь можно сократить числитель и знаменатель на 3n и в 4n степени
Получим дробь, которую преобразуем по свойству степеней:
14−2∙3−1 = 42∙311=16∙3=48
Ответ: 48pазбирался: Базанов Даниил | обсудить разбор
Задание OM2003
Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:
(х – 2)2 – 3<0
У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:
х2 – 4х+4 – 3 <0
х2 – 4х+1 <0
Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел (<0)
Для этого найдем нули функции, решая с помощью дискриминанта:
Д=(-4)2 — 4∙1∙1=16-4=12
х1=4− √122=2(2−√3)2=2−√3
Знаем, что х2 будет отличаться только знаком, получим, что х2=2+√3
Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки (2−√3) до точки (2+√3).
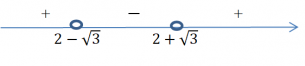
Ответ: (2−√3 ; 2+√3)
pазбирался: Базанов Даниил | обсудить разбор
Задание OM2002
Данное уравнение является квадратным. Но в его условии присутствует квадратный корень, что усложняет нам задачу для нахождения его корней, в том плане, что необходимо увидеть, какие же ограничения на переменную х здесь будут.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного корня): ограничение на х: 5−х≥0
Решаем полученное неравенство: −х≥−5, отсюда х≤5. Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х2−2х+√5−х − √5−х− 24=0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х2−2х− 24=0
Итак, корнями уравнения х2−2х− 24=0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 не≤5, а число минус 4 записываем в ответ нашего уравнения, так как −4≤5 .
Ответ: -4pазбирался: Базанов Даниил | обсудить разбор
Задание OM2001
Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби:
4a−9b+39a−4b+3=5
5(9а – 4b + 3)=4a – 9b+3
Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные):
45a – 20b +15 =4a – 9b+3
45a – 20b – 4a + 9b=3 – 15
Приведем подобные слагаемые:
41a – 11b = — 12
Выпишем выражение, значение которого надо найти: 41a – 11b + 15 и заменим в нем 41a – 11b на число -12, полученное при упрощении нашей дроби:
41a – 11b + 15= — 12 + 15=3. Видим, что значение нашего выражения получилось равным 3.
Ответ: 3pазбирался: Базанов Даниил | обсудить разбор
Задание 20OM21R
Нам дано уравнение третьей степени: х3 + 6х2=4х + 24
В данном уравнении перенесем все слагаемые в одну сторону ( в левую), изменяя при этом знаки: х3 + 6х2 – 4х – 24=0
Теперь сгруппируем слагаемые: (х3 + 6х2) – (4х + 24)=0
Вынесем общий множитель за скобки из каждой группы: х2(х + 6) – 4(х + 6)=0
Вынесем за скобки выражение (х + 6): (х + 6)(х2– 4)=0
Приравняем каждый множитель к нулю и решим полученные уравнения:
х + 6=0 и х2– 4=0
х=-6 и х2=4, отсюда х1,2=±2
Ответ: 2pазбирался: Базанов Даниил | обсудить разбор
Задание OM2106o
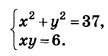
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном уравнении с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х2 на а. Решаем полученное квадратное уравнение.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
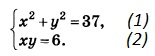
Из (2) выражаем у через х:
![]()
Полученное выражение для у подставляем в (1):
![]()
Выполним преобразования:
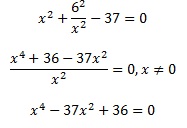
Выполним замену: х2= , а≠0 .
Получим:
а2–37а+36=0
По теореме Виета а1=1, а2=36
Отсюда имеем:
х2=1 → х=±1 → х1=–1, х2=1
х2=36 → х=±6 → х3=–6, х4=6
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у:
![]()
Корни системы: (–1; –6), (1; 6), (–6; –1), (6; 1)
Ответ: 16pазбирался: Базанов Даниил | обсудить разбор
Задание OM2105o
(3х–7)2≥(7х–3)2
Алгоритм решения:
- Используя формулу сокращенного умножения для квадрата разности, раскрываем скобки в левой и правой части неравенства.
- Группируем элементы (слагаемые) неравенства: слагаемые с «х» должны оказаться в левой части, свободные члены – в правой. Приводим подобные.
- Решаем полученное неравенство.
Решение:
9х2–42х+49≥49х2–42х+9
9х2–42х–49х2+42х≥9–49
–40х2≥–40
х2≤1
х≤|1| → –1≤x≤1 → xϵ[–1; 1]
![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM2104o
(х–2)4+3(х–2)2–10=0
Алгоритм решения:
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Решение:
(х–2)4+3(х–2)2–10=0
Выполняем замену: (х–2)2=а.
Получаем:
а2+3а–10=0
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
а1+а2=–b, a1·a2=c.
Здесь а1, а2 – корни этого уравнения, b=3, c=–10.
Отсюда получаем: а1=2, а2=–5.
Возвращаемся к переменной х. Поскольку (х–2)2=а, то получим:
1) (х–2)2=2

2) (х–2)2=–5
это уравнение корней не имеет, т.к. нельзя извлечь корень из отрицательного числа
Корни уравнения: ![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM2103o
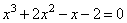
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: ![]() — подходит это и есть один из корней.
— подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
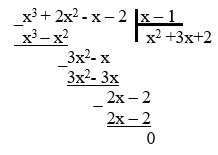
5. Получаем квадратный трехчлен
x2 +3x+2
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
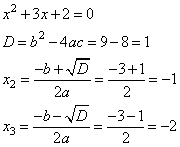
7. Получили три корня -2; -1; 1.
Ответ: -2pазбирался: Базанов Даниил | обсудить разбор
Задание OM2102o
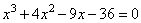
5. После деления получаем квадратный трехчлен:
Ответ: 3pазбирался: Базанов Даниил | обсудить разбор
Задание OM2101o
x4 = (4x - 5)2
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x4 — (4x — 5)2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х2 – (4х-5))( х2 + (4х-5)) = 0, или (х2 – 4х+5)(х2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х2 – 4х+5 = 0 и х2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b2-4ac = 16-20 = — 4, это означает, что первое уравнение х2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
![]()
Определим корни второго уравнения:
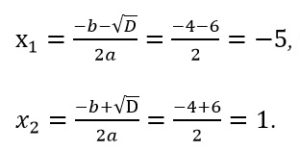 Получили два корня: -5; 1.
Получили два корня: -5; 1.
pазбирался: Базанов Даниил | обсудить разбор
👀 31.2k
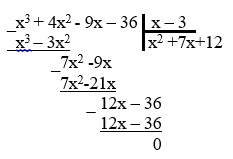
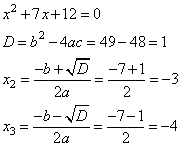
В последнем задание при решении уравнения х+6=0 допущена ошибка: х=6. Правильный ответ х= — 6. Возможно это — описка. В остальном всё хорошо! В заданиях 2 и 3 в моем классе я использую лёгкий способ — способ группировки. Важно правильные решение и ответ! А ВЫ — умница! СПАСИБО!