Задания 1-5 ОГЭ по математике
Первичный бал: 5 Сложность (от 1 до 3): 2 Среднее время выполнения: 12 мин.
Данные задания направлены на изучение информации, представленной в графическом виде, после изучения которой, учащийся должен произвести определенные расчеты. Выполнять необходимые записи при выполнении задания можно прямо в контрольно-измерительном материале. В бланк записываются только ответы.
Задание OM1-520221 (листы бумаги)
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее.
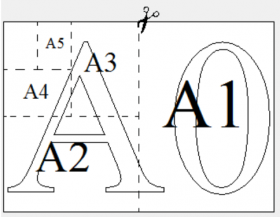
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранились при уменьшении или увеличении шрифта при изменении формата листа.
Задание №1. В таблице даны размеры (с точностью до мм) четырех листов, имеющих форматы А0, А1, А3 и А4.
| Номер
листа |
Длина (мм) | Ширина (мм) |
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
| А0 | А1 | А3 | А4 |
Решение
Из условия задачи необходимо понять, что лист наибольшего формата – это А0, а дальше по возрастанию цифры уменьшается формат листа. Следовательно, для установления соответствия мы находим сначала самый наибольший по длине и ширине лист, это будет лист номер 3 (размеры выделены красным в таблице),
| Номер
листа |
Длина (мм) | Ширина (мм) |
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
вписываем его в табличку под А0; продолжаем так же, находя следующий наибольший из оставшихся – это лист под номером 4 (выделен синим), значит это А1; следующим будет лист под номером 2 (зеленый), значит это А3. Ну и самый наименьший остался (не выделен) – это номер 1, значит он и есть А4.
| А0 | А1 | А3 | А4 |
| 3 | 4 | 2 | 1 |
В бланк ответ записываем в следующем порядке: 3421
Задание №2. Сколько листов формата А3 получится из одного листа формата А1?
Решение
Из условия задачи и рисунка к условию нужно понимать, что из листа А0 можно получить два листа формата А1, разрезав А0 пополам параллельно меньшей стороне. И так далее, разрезая листы. Нам надо узнать, сколько листов А3 получится из А1.
Значит, из А1 получаем два листа формата А2; теперь разрезаем оба листа формата А2 и получаем четыре листа формата А3.
Данную задачу можно решить другим способом, используя формулу N=2(y-x) , где N – это количество искомых листов, y и x – это цифровые значения форматов. В нашем случае получается, что N=2(3-1)=22=4.
Ответ: 4
Задание №3. Найдите площадь листа формата А4. Ответ дайте в квадратных сантиметрах.
Решение
Для нахождения площади листа А4 нужно знать длину и ширину листа данного формата. Из условия задачи номер 1 возьмем эти данные. Лист формата А4 указан под номером 1, следовательно, его размеры 297 мм (длина) и 210 мм (ширина). Так как ответ надо дать в квадратных сантиметрах, то переведем наши данные из миллиметров в сантиметры (1 см=10 мм), то есть 297 мм=29,7 см; 210 мм=21 см. Теперь найдем площадь, зная, что лист имеет форму прямоугольника, умножим длину на ширину: 29,7×21=623,7 кв.см
Ответ: 623,7
Задание №4. Найдите длину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Решение
Найти длину листа формата А2 можно двумя способами.
1 способ: берется лист А1 и разрезается параллельно меньшей стороне, значит большей стороной А2 становится меньшая сторона листа А1, т.е. (берем размеры из задания 1) лист А1 – это 841 мм на 594 мм, следовательно, меньшая его сторона 594 мм становится длиной (большей стороной) листа А2. Округлим его до ближайшего целого числа, кратного 10. Итак, в соответствии с правилом округления, 594 ≈590.
2 способ: Берется 2 листа формата А3 (420 мм на 297 мм) и из них составляется 1 лист формата А2, следовательно две наименьшие стороны листа А3 составят наибольшую сторону (длину) листа А2, значит 297 умножаем на 2 и получаем 594. Дальше округляем 594 до ближайшего целого числа, кратного 10, получаем 590.
Ответ: 590
Задание №5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.
Решение
Так как листы подобны, то отношение высот шрифтов будет таким же, как отношение длины (ширины) листов двух данных форматов.
По условию задания мы работаем с листами форматов А3 и А4. Значит, нам нужны длины этих листов, возьмем их из задания №1.
Итак, длина листа А3 равна 420 мм, листа А4 – 297 мм. Высота шрифта на формате А3 по условию не известна, а высота шрифта на листе А4 равна по условию 15 пунктов (мы привыкли называть это размером шрифта).
Можно составить краткую запись для более удобного нахождения решения:
А3 – 420 мм – х пунктов
А4 – 297 мм – 15 пунктов
Отсюда можно составить пропорцию: 420297=х15; откуда х=420×15297=21, 2…≈21 (в условии сказано, что размер шрифта нужно округлить до целого).
Для проверки можно прикинуть, что раз лист А3 больше, чем лист А4, значит и шрифт на нем должен быть больше, что у нас и получилось, так как 21 больше 15.
Для решения данной задачи можно использовать не только длину листов, но и их ширину.
Так, например, в нашем случае:
А3 – 297 мм – х пунктов
А4 – 210 мм – 15 пунктов
Отсюда можно составить пропорцию: 297210=х15; откуда х=297×15210=21, 2…≈21 (в условии сказано, что размер шрифта нужно округлить до целого).
Видно, что результат получился одинаковый.
Ответ: 21
Общие советы и рекомендации к данному виду задач
Не нужно пугаться самого условия заданий, надо помнить, что просто самый большой лист – это лист формата А0 (в привычном для нас виде – это обычный «ватман»), а дальше он разрезается и из него получаются листы меньшего формата, а числовые значения увеличиваются, т.е. А1, А2, А3 и так далее.
Если при решении задачи на нахождение количества листов не вспомнили формулу, то просто рисуем листы и «режем» их на своих рисунках, результат будет одинаковый!
Условие задания 5 дается нам для общего развития, самое главное в нём – это размер шрифта (пункты) и необходимые для решения форматы листов. А составление пропорции — это просто, главное – не ошибиться в отношении, то есть – большего к большему или меньшего к меньшему!
pазбирался: Базанов Даниил | обсудить разбор
Задание 15OM21R

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Ответ: 11
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Ответ: 4
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Ответ: 48
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер
магазина |
Расход
краски |
Масса краски
в одной банке |
Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: 30500
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15МО10 (ОСАГО)
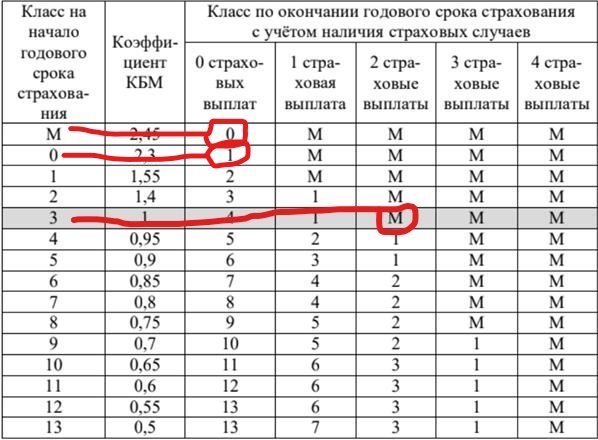
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей:
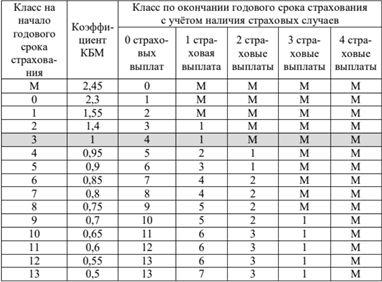
Задание №1. Павел страховал свою гражданскую ответственность три года. В течение первого года были сделаны две страховые выплаты, после этого выплат не было. Какой класс будет присвоен Павлу на начало четвёртого года страхования?
Решение
По условию задачи имеем, что всегда изначально присваивается водителю 3 класс, поэтому в начале первого года Павлу был присвоен класс 3. Начинаем работать с таблицей. Находим в 1 столбце 3 класс.
В течение первого года были сделаны две страховые выплаты, то есть это значит, что у него было два нарушения ПДД. От класса 3 двигаемся по строке горизонтально до пересечения со столбцом «2 страховые выплаты». Видно, что после двух выплат в течение первого года на начало второго года Павлу был присвоен класс М.
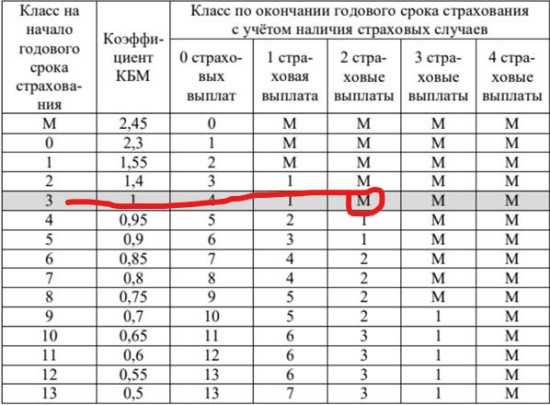
Теперь находим в первом столбце класс М и двигаемся от него горизонтально до пересечения со столбцом «0 страховых выплат», так как в течение второго года у него не было страховых выплат. Получается, что у него на начало 3 года 0 класс.
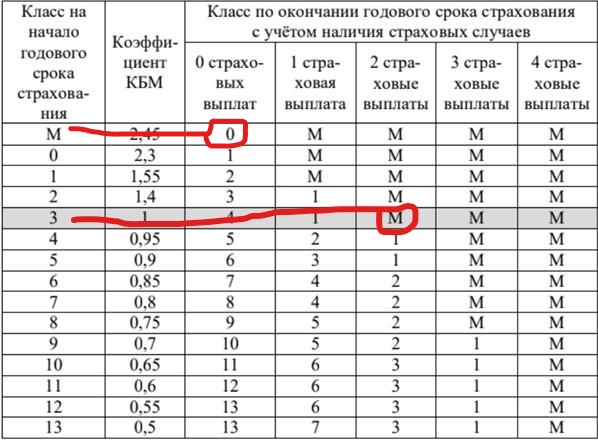
В течение третьего года Павел также не делал страховых выплат, следовательно, находим в таблице в 1 столбце нулевой класс и двигаемся по строке горизонтально до пересечения со столбцом «0 страховых выплат». Получаем, что на начало четвёртого года Павлу будет присвоен класс 1.
Следовательно, ответ в нашем задании – 1 класс.
Ответ: 1
Задание №2. Чему равен КБМ на начало четвёртого года страхования?
Решение
Начнем с того, что такое КБМ. Об этом сказано в условии задачи: КБМ – коэффициент бонус-малус, который зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год.
По условию мы знаем, что в начале первого года Павлу был присвоен класс 3. А по решению 1 задачи имеем: после двух выплат в течение первого года на начало второго года Павлу был присвоен класс М. Поскольку в течение второго года Павел не делал страховых выплат, на начало третьего года Павлу был присвоен класс 0. В течение третьего года Павел также не делал страховых выплат, следовательно, на начало четвёртого года Павлу будет присвоен класс 1. Работаем с таблицей, находим 1 класс в первом столбце и идем до пересечения со столбцом «КБМ»: КБМ на начало четвёртого года страхования равен 1,55.
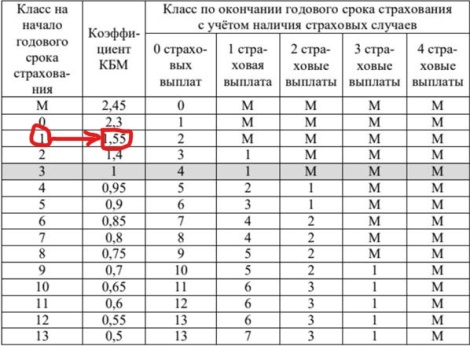
Ответ: 1,55
Задача №3. Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу)
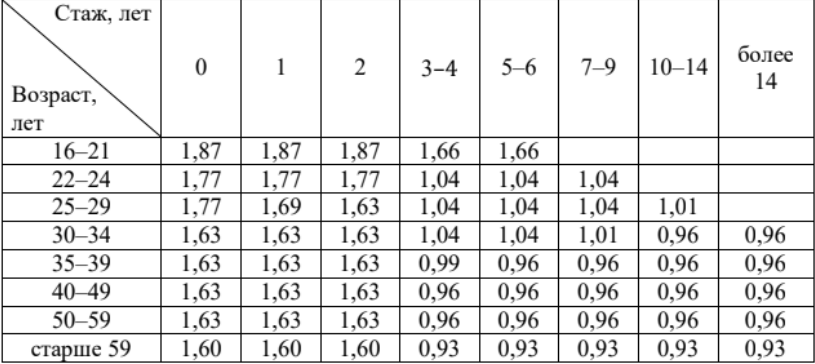
Когда Павел получил водительские права и впервые оформил полис, ему было 24 года. Чему равен КВС на начало 4-го года страхования?
Решение
Когда Павел впервые получил права и оформил полис, ему было 24 года, значит, на начало второго года ему было 25, на начало третьего – 26, а на начало 4-ого – 27 лет. Следовательно, на начало 4 года страхования он будет попадать в возрастную категорию 25−29 лет (смотрим таблицу), а его стаж будет попадать в промежуток 3−4 года. Совмещаем по таблице эти две категории и на пересечении находим, что КВС равен 1,04.
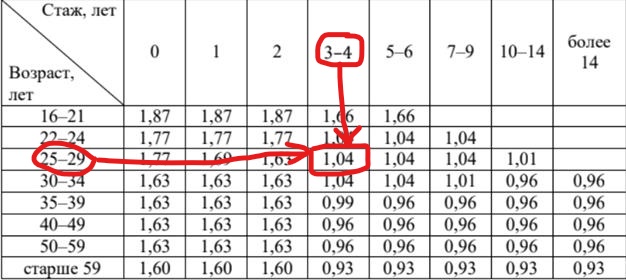
Ответ: 1,04
Задача №4. В начале третьего года страхования Павел заплатил за полис 18745 руб. Во сколько рублей обойдётся Павлу полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Решение
По условию задачи сказано, что стоимость полиса получается умножением базового тарифа на несколько коэффициентов – КБМ и КВС.
Зная, что в начале третьего года страхования Павел заплатил за полис 18745 руб, а значение базового тарифа не меняется, мы можем рассчитать стоимость страховки. Для этого нужно знать базовый тариф.
Итак, сначала найдём КБМ и КВС на начало третьего года.
По решению задачи 2 у нас известно, что на начало 3-го года Павел имел 0 класс, следовательно, по таблице — КБМ будет равен 2,3.
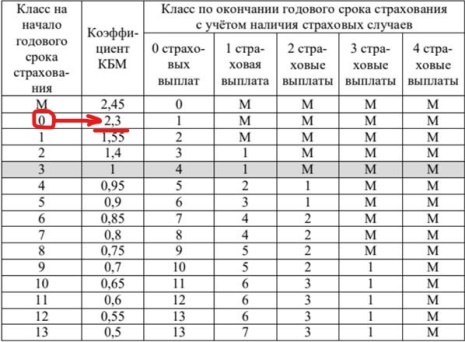
Дальше надо найти КВС: так как мы ищем его на начало 3-его года, то стаж водителя был 2 года, а возраст 26 лет (смотрим задачу 3), он попадает в категорию 25-29. Итак, работаем с таблицей и находим, что КВС на начало третьего года равен 1,63.
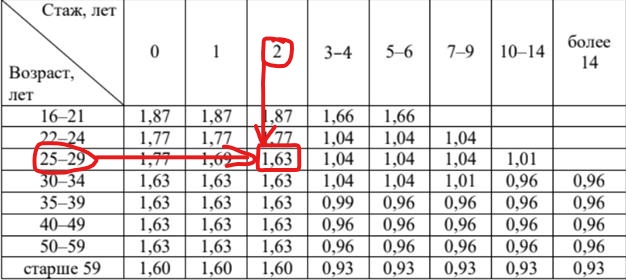
Теперь, зная, что страховка была 18745 руб, КБМ равен 2,3, а КВС равен 1,63, составим равенство: 18745=х•2,3•1,63, где х – это базовый тариф.
Находим х, как неизвестный множитель, разделив 18745 на произведение 2,3•1,63, т.е.
Х=18745: (2,3•1,63)=5000 рублей
Теперь можно находить стоимость страховки на 4-й год.
Итак, базовый тариф равен 5000 руб, КБМ на начало четвёртого года равен 1,55 (задача 2), КВС на начало четвёртого года равен 1,04 (задача 3). Значит, на начало четвёртого года стоимость полиса равна: 5000∙1,55∙1,04=8060 рублей
Ответ: 8060 рублей
Задача №5. Павел въехал на участок дороги протяжённостью 2,7 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 60 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Павел въехал на участок в 11:03:16, а покинул его в 11:05:31. Нарушил ли Павел скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Решение
Чтобы определить, были ли нарушения ПДД на данном участке пути, нужно знать, с какой скоростью он его проехал. Для нахождения скорости нам нужно знать время и расстояние.
По условию задачи мы знаем, что расстояние равно 2,7 км. Вычислим время: так как на участок Павел въехал в 11:03:16, а покинул его в 11:05:31, то вычтем из11:05:31 число11:03:16, получим 2:15, то есть 2 минуты 15 секунд – это 135 секунд. Нам надо перевести их в часы: в 1 часе 3600 секунд, значит, 1353600=380.
Найдем теперь скорость, нужно разделить расстояние 2,7 км на время, т.е. на 380 часа. Итак, 2,7:380=2710×803=72 км/ч. Видно, что на участке с разрешенной скоростью 60 км/ч Павел ехал со скоростью 72 км/ч. Он нарушил скоростной режим, превысив её на 12 км/ч.
Ответ: 12
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15МО09 (теплицы)
Виктор Николаевич решил построить на дачном участке теплицу длиной 6 метров. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы он заказал металлические дуги в форме полуокружности длиной 5 метров каждая, а также покрытие для обтяжки.
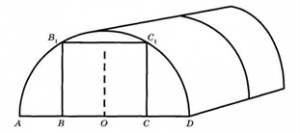
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется сделать вход, который показан на рисунке прямоугольником ВВ1С1С, где точки В,О и С делят отрезок АД на равные части.
Внутри теплицы Виктор Николаевич планирует сделать три грядки по длине теплицы – одну центральную широкую и две по узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых нужно купить тротуарную плитку размером 25 см 25 см.
Задание №1. Какое наименьшее количество дуг надо заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение
На рисунке дуги выделены красным цветом и показано, что расстояние между ними не более 80 см.
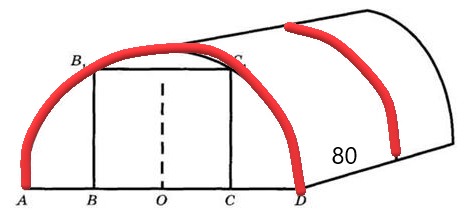
Зная, что длина теплицы 6 метров, переведем её в сантиметры: 6м=600 см. Теперь разделим 600 см на 80 см, получим 7,5. Округлим до целого числа и получим 8, но это не количество дуг, а количество расстояний (отрезков) между ними. Далее нужно прибавить единицу, чтобы получить точное количество: 8+1=9 дуг.
Если способ с рисунком теплицы не совсем понятен, то можно изобразить дуги точками на отрезке вот таким образом.

Ответ: 9
Задание №2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение
По условию задачи знаем, что в теплице будет три грядки, следовательно, будет две дорожки, ширина которых по условию 50 см. Длина каждой дорожки равна длине теплицы, т.е. 600 см.
Зная длину и ширину дорожки, можно найти её площадь: 600×50=30000 см2. Таких дорожек у нас две, значит 30000×2=60000 см2.
По условию задачи известно, что тротуарная плитка имеет размеры 25 см ×25 см. Можно найти площадь одной плитки: 25 см ×25 см=625 см2.
Теперь находим количество плиток для двух дорожек: 60000:625=96 плиток.
Так как сказано, что плитки продаются в упаковках по 10 штук, то разделим 96 на 10, получим 9,6. Необходимо округлить результат до целого числа, так как отдельно несколько плиток нам не продадут, поэтому 9,6≈10.
Ответ: 10
Задание №3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение
Ширина теплицы – это диаметр полуокружности. По условию задачи Виктор Николаевич покупал дуги длиной 5 метров, значит, длина полуокружности и есть 5 метров.
Вспомним формулу, которая связывает длину окружности и радиус: С=2πR, также можно воспользоваться и формулой С=πd, так как нам надо найти ширину теплицы, т.е. диаметр.
Подставим значения в формулу, помня о том, что полная длина окружности будет равна 10 м: 10=3,14d. Отсюда d=10:3,14=3,184…≈3,2 (так как по условию требуется округлить до десятых).
Ответ: 3,2
Задание №4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.
Решение
Покажем на рисунке, как выглядят грядки и дорожки внутри теплицы, расставим известные данные: 50 см – по условию, а 320 см – из решения задания №3.
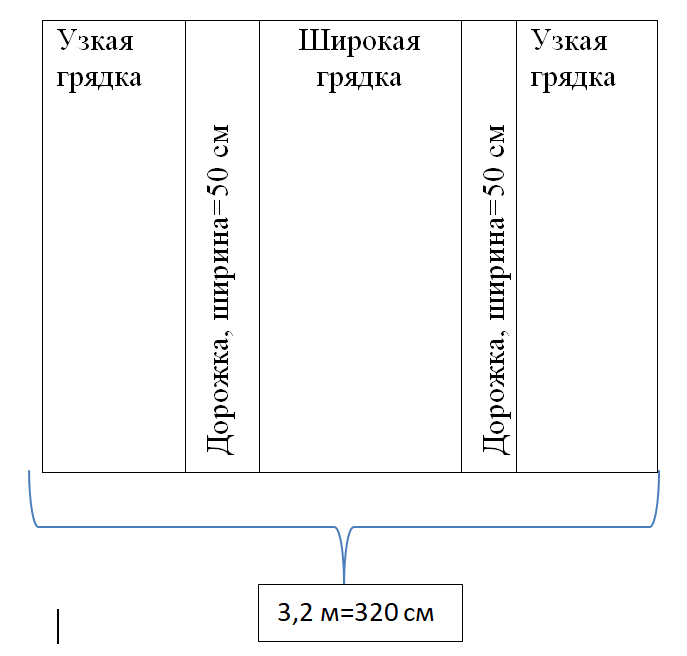
Для удобства решения определим ширину всех грядок вместе, то есть уберем ширину дорожек: 320-50-50=220 см.
По условию задачи ширина центральной грядки относится к ширине узкой грядки как 5:3, т.е. можно сказать, что на центральную грядку (широкую) приходится 5 частей, а на крайние грядки (узкие) по 3 части. Значит, всего на три грядки приходится 3+5+3=11 равных частей. Так как вся ширина грядок 220 см, то 220:11=20 см ширина одной части. Значит, ширина узкой грядки будет равна 20 см×3=60 см.
Ответ: 60 см
Задание №5. Сколько квадратных метров пленки необходимо купить для передней и задней стенок теплицы, если с учетом крепежа ее нужно брать с запасом 15%? Ответ округлить до десятых.
Решение
Передняя и задняя стенки теплицы являются полукругами одинакового диаметра, следовательно, два полукруга вместе – это круг, диаметр которого (ширина теплицы) мы нашли в задаче №3, т.е.3,2 метра. Площадь круга находится по формуле S=πR2. Зная, что диаметр равен 3,2 м, найдем радиус: 3,2:2=1,6 м. Подставим в формулу данные и найдем площадь круга: S=3,14×1,62=8,0384 м2
По условию задачи сказано, что с учетом крепежа пленку надо покупать с запасом 15%. Найдем 15% от данного числа, переведя 15% в десятичную дробь: 0,15×8,0384=1,20576.
Теперь складываем площадь круга и найденные 15%: 8,0384+1,20576=9,24416.
Так как ответ надо округлить до десятых, то получим: 9,24416≈9,2
Ответ: 9,2
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15MO08 (зонт)

Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рисунок 1). Сферическая форма в раскрытом состоянии достигается за счет гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц (а). Оно оказалось равно 38 см. Высота купола зонта h (рисунок 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Задание №1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рисунок 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Решение
Так как длина зонта складывается из длины ручки и трети длины спиц, то можно найти треть длины спиц: 25 – 6,2=18,8 (см).
Так как это треть, то всю длины спицы можно найти, умножив данное число на 3: 18,8×3=56,4 (см) — длина спицы.
Ответ: 56,4
Задание №2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение
Для нахождения площади поверхности зонта надо знать площадь каждого треугольника (клина), так как из них состоит поверхность зонта.

На рисунке в условии задачи мы видим равнобедренный треугольник, у которого длина стороны а=38 см. Для нахождения площади треугольника нам нужны сторона и высота, проведенная к ней. Высота (выделена красным) по условию равна 53,1 см.
Теперь воспользуемся формулой площади треугольника (она есть в справочном материале) S=ah2=38×53,12=1008,9.
Знаем, что всего таких треугольников 8, найдем площадь всей поверхности: 1008,9×8=8071,2 см2. Так как ответ нужно дать с округлением до десятков, то получим, что 8071,2≈8070.
Ответ: 8070
Задание №3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.
Решение
Обратимся к рисунку №2, чтобы увидеть, чем конкретно является радиус сферы купола на нём.
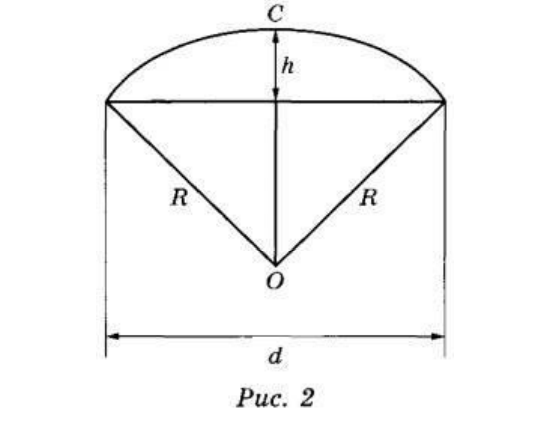
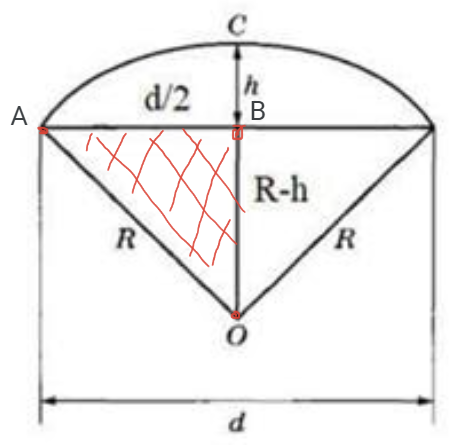
Сделаем на рисунке дополнительные обозначения: точки А и В. Получим прямоугольный треугольник АОВ, у которого гипотенуза АО=R по условию, катет АВ=d/2, тогда катет ОВ=ОС – СВ, то есть ОВ=R-h.
Теперь по теореме Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов) составим равенство: АО2=АВ2+ОВ2; подставим наши данные:
R2=(d2)2+ (R-h)2
Упростим наше выражение, подставим в него значения из условия задачи (h=25, d=100):
R2=d24+ R2-2Rh + h2 (возвели в квадрат; использовали формулу сокращенного умножения (а – в)2=а2-2ав+в2)
R2=10024+ R2-2R× 25+ 252 (подставили числовые значения)
R2=2500+ R2-50R+ 625 (взаимоуничтожили R2 и перенесли 50R в левую часть)
50R=3125
R=3125:50=62,5
Ответ: 62,5
Задание №4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh , где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение
Для решения данной задачи у нас есть всё в её условии – формула S = 2πRh и данные для того, чтобы подставить в эту формулу. Так, радиус мы нашли в задании 3 (62,5); высота известна по условию, она равна 25, число π берем как 3,14.
S = 2×3,14×62,5×25=9812,5
Так как надо ответ округлить до целого, то 9812,5≈9813
Ответ: 9813
Задание №5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение
Рассмотрим, в чем же смысл данного задания. У нас есть рулон ткани, из которой шьют зонты, отрезая необходимое количество. И, конечно же, от рулона ткани останутся обрезки. Требуется найти, сколько процентов ткани такого рулона пошло на эти обрезки.
Начнем с рулона: известна длина и ширина, следовательно, можно найти площадь всего этого рулона, т.е. 3500×80=280000 см2. Обратите внимание, что мы взяли 35 м=3500 см.
Теперь будем «шить» зонты, у нас их 29 штук по условию задания. Каждый зонт состоит из 8 клиньев-треугольников, то есть всего таких клиньев нам понадобится 8×29=232 штуки. Зная, по условию задания, что на 1 клин-треугольник требуется 1050 кв.см ткани, найдем, сколько её понадобится на наши 232 клина: 232×1050=243600 см2.
Теперь из общей площади нашего рулона ткани вычтем площадь ткани для зонтов:
280000 – 243600=36400 см2, это столько ткани-обрезков. Осталось ответить на вопрос задания – сколько процентов ткани рулона пошло в обрезки? Для этого данное число разделим на общую площадь ткани в рулоне и не забудем умножить на 100, так как находим ответ в процентах: 36400:280000×100=13%
Ответ: 13%
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15MO07 (печь для бани)
Хозяин дачного участка строит баню с парным отделением. Размеры парного отделения: длина и ширина по 2,5 м, высота 2,2 м. Для разогрева парного помещения можно использовать электрическую или дровяную печь. Три возможных варианта даны в таблице.
| Печь | Тип | Отапливаемый объем, куб.м | Масса, кг | Цена, руб |
| Орион | Дровяная | 6-12 | 45 | 17000 |
| Кентавр | Дровяная | 10-15 | 65 | 21000 |
| Ока | Электрическая | 8-14 | 14 | 20000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдется в 5000 рублей. Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 2500 киловатт-часов электроэнергии по 4 руб. за 1 киловатт-час, а дровяная печь за год израсходует 1,8 куб. м дров, которые обойдутся по 1000 руб. за 1 куб. м.
Задание №1. Найдите объем парного отделения строящейся бани (в куб. м).
Решение
Для решения данного задания надо понимать, что парное отделение бани представляет собой объемную геометрическую фигуру – прямоугольный параллелепипед, а для нахождения объема прямоугольного параллелепипеда надо знать длину, ширину и высоту, затем применяем формулу объема V=abc, где a-длина, b-ширина, c-высота. Эти данные есть в самом начале задачи: длина и ширина по 2,5 м, высота 2,2 м.
Имея эти данные, находим объем: 2,5×2,5×2,2=13,75 куб.м.
Ответ: 13,75
Задание №2. На сколько рублей дровяная печь, подходящая по отапливаемому объему парного отделения, обойдется дешевле электрической с учетом установки?
Решение
Дровяная печь, подходящая по отапливаемому объему парного отделения, это печь «Кентавр», с объемом 13,75 куб.м, а эта величина как раз подходит, так как она удовлетворяет неравенству 10<13,75<15.
Нам надо сравнить цены двух печей – «Кентавр» и «Ока» с учетом их установки. По условию задачи для дровяной печи установка не требуется, а для установки электрической печи потребуется подведение специального кабеля, что обойдется в 5000 рублей. Можно разбор решения записать в виде таблицы, где и найдем разницу в цене:
| Печь | Тип | Цена, руб | Установка | Итого | Разница |
| Кентавр | Дровяная | 21000 | 0 руб | 21000 руб | 25000-21000=4000 руб |
| Ока | Электрическая | 20000 | 5000 руб | 25000 руб |
Ответ: 4000
Задание №3. На сколько рублей эксплуатация дровяной печи, которая подходит по отапливаемому объему парного отделения, обойдется дешевле эксплуатации электрической в течение года?
Решение
В данной задаче речь идет об эксплуатации этих же печей, то есть какие затраты в год требуются для каждой из этих печей. А найти надо разницу в стоимости эксплуатации этих печей.
В условии задачи сказано, что за год электрическая печь израсходует 2500 киловатт-часов электроэнергии по 4 руб. за 1 киловатт-час, а дровяная печь за год израсходует 1,8 куб. м дров, которые обойдутся по 1000 руб. за 1 куб. м.
Находим затраты на электропечь: 2500 киловатт-часов электроэнергии по 4 руб. за 1 киловатт-час, это 2500×4=10000 руб.
Находим затраты на дровяную печь: 1,8 куб. м дров по 1000 руб. за 1 куб. м., это 1,81000=1800 руб.
Теперь находим разницу: 10000 – 1800=8200 руб
Ответ: 8200
Задание №4. Доставка печи из магазина до участка стоит 600 рублей. При покупке печи ценой выше 20000 рублей магазин предлагает скидку 5% на товар и 45% на доставку. Сколько будет стоить покупка печи «Кентавр» вместе с доставкой на этих условиях?
Решение
Требуется определить стоимость покупки печи «Кентавр» с доставкой до участка. По условию задачи печь стоит 21000 рублей, а это выше 20000 руб, поэтому положена скидка, как на товар, так и на доставку.
Найдем, сколько будет стоить печь со скидкой 5%:
21000:100×5=1050 руб – скидка на печь
21000 – 1050=19950 руб – стоимость печи со скидкой
Найдем, сколько будет стоить доставка со скидкой 45%:
600:100×45=270 руб – скидка на доставку
600 – 270=330 руб – доставка печи со скидкой
Найдем, сколько будет стоить печь с доставкой:
19950+330=20280 руб
Ответ: 20280
Задание №5. Хозяин выбрал дровяную печь. Чертеж печи показан на рис. 2. Размеры указаны в сантиметрах.
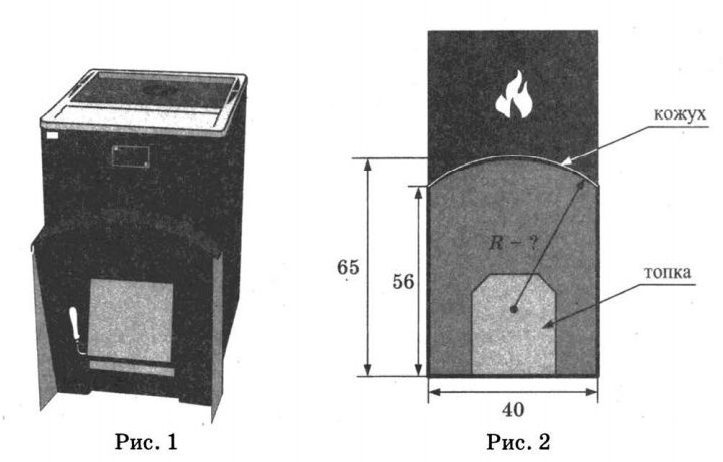
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности (см. рис.). Для установки печки хозяину понадобилось узнать радиус R закругления арки. Размеры кожуха показаны на рисунке. Найдите радиус в сантиметрах; ответ округлите до десятых.
Решение
На рисунке 2 нам показана именно та часть, с которой мы должны работать на «языке» геометрии. Это показана часть окружности определенного радиуса (он показан стрелкой и буквой R), который мы и должны найти. Если сделать на рисунке свои дополнительные построения, то они будут выглядеть следующим образом (рис.3):
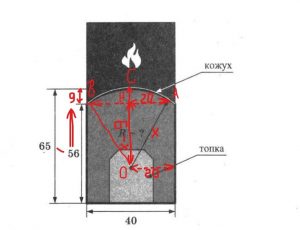
Введем дополнительные обозначения: радиусы пусть будут ОА, ОС, ОВ. Они нам неизвестны. АВ – это хорда, по рисунку видно, что она равна 40. У нас есть равнобедренный треугольник АОВ (АО=АВ=R), ОН – высота по построению.
Рассмотрим треугольник АОН, где угол Н – прямой. Пусть в нем гипотенуза ОА (он же радиус), которая нам неизвестна, будет обозначена х. Видим, что катет АН=20 см, так как АВ=40, а высота ОН, проведенная к основанию АВ, является медианой (свойство равнобедренного треугольника). Найдем катет ОН: слева на рисунке указаны две длины – 65 и 56, а отрезок СН как раз является разницей между ними, т.е. СН=65-56=9. Значит, чтобы найти катет ОН, надо из ОС (а это радиус, который мы обозначили за х) вычесть 9, таким образом, получим, что ОН=х-9.
Итак, в прямоугольном треугольнике имеем: гипотенуза равна х, катеты равны 20 и (х-9). Применим теорему Пифагора (квадрат гипотенузы равен сумме квадратов катетов):
х2=202+ (х-9)2
х2=400 + х2 – 18х + 81 (возвели в квадрат числа и разность двух выражений)
0=481 – 18х (взаимоуничтожили х2 в левой и правой частях уравнения)
18х=481 (перенесли слагаемое с переменной влево, изменяя знак на противоположный)
х=481:18 (выполнили нахождение неизвестного множителя действием деления)
х=26,7222… (нашли приближенное значение корня уравнения)
Значит, радиус, который обозначали за х, будет равен приближенно 26,722…
Так как по условию задачи нам надо округлить число до десятых, то по правилу округления, ответ будет 26,7.
Ответ: 26,7
Общие советы и рекомендации к данному виду задач
Необходимо помнить простое правило нахождения объема прямоугольного параллелепипеда, а также то, что наши обычные комнаты, бани и парные имеют форму прямоугольного параллелепипеда.
Отличайте покупку печей от их эксплуатации. При покупке оплачивается товар и необходимые к нему дополнительные элементы (например, провод). А эксплуатация – это использование печи, т.е. при этом происходит оплата за свет (если печь электрическая) или за дрова (если печь дровяная).
При решении задания 5 сделайте на своём рисунке дополнительное построение до прямоугольного треугольника, обозначьте радиус (гипотенузу) за х, найдите катеты. При нахождении одного катета просто поделите пополам ширину печки, а при нахождении второго — вычтите из х разницу в длинах, указанных на рисунке слева. Составьте равенство, используя формулировку теоремы Пифагора. Желаем удачи!
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15MO06 (план квартиры)
На рисунке изображен план двухкомнатной квартиры в многоэтажном жилом доме. Сторона каждой клетки на плане равна 0,5 м. Вход в квартиру находится в прихожей. Слева от входа расположен санузел, а справа гостиная, кухня и спальня. На кухне есть выход в застекленную лоджию. Из всех помещений в квартире гостиная занимает наибольшую площадь.
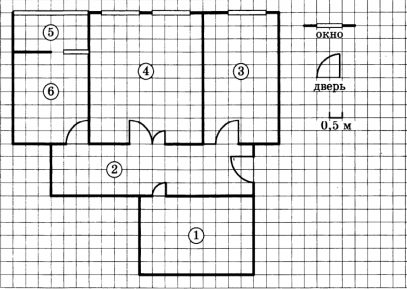
Задание №1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
| Объекты | спальня | лоджия | кухня | гостиная | санузел |
| Цифры |
Решение
Прежде, чем искать на плане квартиры необходимые объекты, необходимо обратить внимание на то, как на нём обозначены двери и окна, так как нам необходимо начать поиск объектов от входной двери. Далее мы работаем по тексту задачи и плану одновременно, подписывая каждый из объектов, так как они пригодятся нам при решении всех пяти заданий.
Итак, входная дверь находится на плане справа, значит, она ведет нас в прихожую, следовательно, прихожая обозначена цифрой 2. По тексту сказано, что слева от входа расположен санузел, значит, это объект под № 1. Все остальные объекты находятся справа от прихожей. Работаем теперь с ними. Известно, что на кухне есть выход в застекленную лоджию (обратим внимание, как обозначено окно), значит, на плане кухня будет под №6, а из неё лоджия — № 5. Далее сказано, что из всех помещений в квартире наибольшую площадь занимает гостиная, следовательно, выбираем из оставшихся объектов под № 3 и № 4 наибольший, это № 4 (гостиная). Оставшийся объект под № 3 — это спальня.
Переходим к заполнению таблицы:
| Объекты | спальня | лоджия | кухня | гостиная | санузел |
| Цифры | 3 | 5 | 6 | 4 | 1 |
Записываем в ответ номера объектов без символов и пробелов.
Ответ: 35641
Задание №2. Найдите ширину остекления лоджии. Ответ дайте в сантиметрах.
Решение
Из задания 1 знаем, что лоджия это объект под номером 5. Также по указанным на плане символам видно, как обозначено окно. Ширина остекления лоджии на плане составляет 6 клеток, а одна клетка – это 0,5 м, значит, умножаем 0,5м на 6 и получаем 3 м. В задании сказано, что надо ответ дать в сантиметрах. Зная, что в 1 метре 100 см, получаем, что 3 метра – это 300 см
Ответ: 300
Задание №3. Плитка для пола размером 25 см ×10 см продаётся в упаковках по 16 штук. Сколько упаковок плитки понадобится, чтобы выложить пол санузла?
Решение
Начнем разбираться с упаковками плит для пола. Если одна плитка имеет размер 25 см ×10 см, то площадь 1 такой плитки будет равна 25 см ×10 см=250 см2.
Дальше мы можем узнать, на какую площадь хватит 1 упаковки такой плитки, если их там 16 штук: 250 см2×16=4000 см2.
Теперь найдем площадь пола санузла (объект № 1), которую требуется этой плиткой покрыть:
Длина санузла: 9 клеток×0,5 м=4,5 м
Ширина санузла: 6 клеток×0,5 м=3 м
Площадь санузла прямоугольной формы находим, умножив длину на ширину: 4,5×3=13,5м2
Теперь, чтобы найти, сколько упаковок плитки понадобится, чтобы выложить ею пол санузла площадью 13,5 м2, необходимо разделить площадь пола на площадь плитки в 1 упаковке: 13,5 м2: 4000 см2; видим, что единицы измерения разные. Можно перевести м2 в см2, помня, что если 1м=100 см, то 1м2=10000 см2. Тогда 13,5 м2 = 13,5×10000=135000 см2.
Выполним деление: 135000 см2: 4000 см2=33,75. Знаем, что количество упаковок нам продадут целое, получим, что нам нужно 34 упаковки.
Ответ: 34
Задание №4. Найти площадь, которую занимает спальня. Ответ дайте в квадратных метрах.
Решение
Из условия задания 1 знаем, что спальня – это объект под № 3. Спальня прямоугольной формы, значит, нам надо найти площадь прямоугольника, умножив его длину на ширину.
Длина спальни 10 клеток, а одна клетка 0,5 м, следовательно, 0,5×10=5 м.
Ширина спальни 6 клеток, значит 0,5×6=3 м.
Найдем площадь, умножая длину на ширину, получим 5×3=15 м2
Ответ: 15
Задание №5. На сколько процентов площадь спальни меньше площади прихожей?
Решение
Для решения данной задачи надо найти площадь спальни и площадь прихожей. В задании №4 мы нашли площадь спальни, она равна 15 м2.
По условию задания 1 помним, что прихожая – это объект под номером 2. Прихожая также имеет форму прямоугольника, значит, сосчитаем количество клеток длины и ширины, переведем их в метры и перемножим.
Длина прихожей: 16 клеток×0,5 м = 8 м
Ширина прихожей: 4 клетки×0,5 м = 2 м
Площадь прихожей: 8×2=16 м2
Теперь нам нужно узнать, на сколько процентов площадь спальни меньше площади прихожей.
Пусть прихожая – 16 м2 – 100%,
тогда спальня – 15 м2 – х %
Находим по правилу пропорции, сколько процентов составляет спальня: 15×100:16=93,75%
Найдем разницу (в процентах) между площадями прихожей и спальни:
100% — 93,75%=6,25%
Ответ: 6,25
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15MO05 (шины)
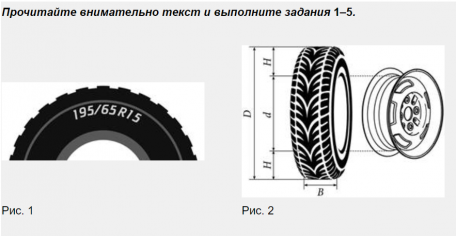
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис.1). Первое число (число 195 в приведенном примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (65 в приведенном примере) – процентное отношение высоты боковины (параметр Н на рисунке 2) к ширине шины, то есть 100•НВ . Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идет число, указывающее диаметр d диска колеса в дюймах ( в 1 дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит внедорожники определенной модели и устанавливает на них колеса с шинами маркировки 215/65 R16.
Задание №1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешенные размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
| 16 | 17 | 18 | |
| 215 | 215/65 | 215/60 | — |
| 225 | 225/65; 225/60 | 225/55 | — |
| 235 | 235/60 | 235/55; 235/50 | 235/50 |
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
Решение
Смотрим по таблице на столбец, где указан диаметр диска – 17 дюймов. Движемся по столбцу вниз и просматриваем первые числа (ширину шины) в маркировках, нам надо найти наибольшую, в последней строке – это число 235. Значит наш ответ 235.
Ответ: 235
Задание №2. На сколько миллиметров радиус колеса с шиной маркировки 215/55 R17 меньше, чем радиус колеса с шиной маркировки 275/50 R17?
Решение
Прежде всего мы должны понимать, что высота колеса (диаметр колеса D) состоит из высоты шины Н, а их две, а также из диаметра диска . Если изобразить это в виде геометрического рисунка, то он будет выглядеть так, как показано на рисунке 2:
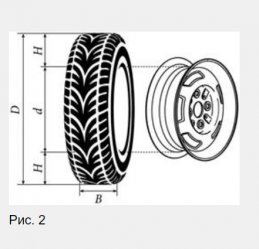
Значит, D=2H + d. Для удобства и последовательного решения задачи лучше составить таблицу, в которой и будем всё решать. В верхней строке записаны данные из условия. В первом столбце выписаны все параметры, которые будем находить.
Таблица 1
| 1 колесо
215/55 R17 |
2 колесо
275/50 R17 |
|
| Высота Н | ||
| Диаметр диска d | ||
| Диаметр колеса D | ||
| Радиус колеса | ||
| Разница в радиусах |
Теперь начинаем заполнять каждую строчку для 1 и 2 колеса, проводя вычисления.
| 1 колесо
215/55 R17 |
2 колесо
275/50 R17 |
|
| Высота Н | Запоминаем: для нахождения высоты выражаем второе число десятичной дробью и умножаем на первое число (так как второе число – процентное отношение высоты боковины к ширине шины). Чтобы выразить число % десятичной дробью, надо разделить его на 100! | |
| 55/100∙215=0,55∙215=118,25 | 50/100∙275=0,5∙275=137,5 | |
| Диаметр диска d | Так как диаметр диска дан в дюймах, то надо умножить последнее число маркировки шины (17) на количество дюймов в 1 мм, т.е. на 25,4 | |
| 17∙ 25,4=431,8 | 431,8 | |
| Диаметр колеса D | В начале решения нашей задачи, мы выяснили как найти диаметр колеса, это надо запомнить! D=2H + d. Находим диаметр в каждом случае, используя данные, которые нашли выше. | |
| 2∙118,25 + 431,8=668,3 | 2∙137,5 + 431,8=706,8 | |
| Радиус колеса | Помним, что радиус, это половина диаметра | |
| 668,3:2=334,15 | 706,8:2=353,4 | |
| Разница между радиусами | Для того, чтобы ответить на вопрос задания, надо найти разность между найденными радиусами | |
| 353,4 – 334,15=19,25 | ||
Ответ: 19,25
Задание №3. На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 235/50 R18?
Решение
Решение данного задания будем строить по принципу задания 2, так как требуется найти разницу в диаметрах между шинами заводской маркировки (смотрим в условии) 215/65 R16 и шинами маркировки 235/50 R18.
Сделаем таблицу, аналогичную таблице 1 (до строки диаметр колеса) и заполним её. Объяснения смотрим по заданию 2.
| 1 колесо
215/65 R16 |
2 колесо
235/50 R18 |
|
| Высота Н | 0,65∙215=139,75 | 0,5∙235=117,5 |
| Диаметр диска d | 16∙ 25,4=406,4 | 18∙ 25,4=457,2 |
| Диаметр колеса D | 2∙139,75 + 406,4=685,9 | 2∙117,5 + 457,2=692,2 |
| Разница между диаметрами колеса | Для того, чтобы ответить на вопрос задания, надо найти разность между найденными диаметрами | |
| 692,2 – 685,9=6,3 | ||
Ответ: 6,3
Задание №4. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение
С данными про колесо автомобиля, выходящего с завода (215/65 R16) мы встретились в задании 3. Надо найти диаметр, он найден в этом же задании 3 (смотрим таблицу с решением этого задания и находим соответствующее значение диаметра). Это значение равно 685,9.
Ответ: 685,9
Задание №5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 225/65 R16? Результат округлите до десятых.
Решение
Пробег автомобиля при одном обороте колеса – это длина окружности колеса. Значит, необходимо найти длину окружности, зная формулу l=2πR (данная формула есть в справочном материале ОГЭ). Зная, что диаметр – это два радиуса, формулу можем записать короче l=πD. Значение числа π не обязательно подставлять в формулу при решении задачи, удобнее использовать буквенное выражение.
Итак, нам надо найти диаметры двух колес, затем найти длины окружностей этих колес и сравнить их в процентном отношении. С маркировкой заводского колеса мы встречались, а данные ко второму колесу нужно найти. Итак, составим таблицу, аналогичную таблице 1, впишем в нее уже найденные значения заводского колеса (из задания 3) и найдем недостающие про «новое» колесо.
| 1 колесо (заводское)
215/65 R16 |
2 колесо
225/65 R16 |
|
| Высота Н | 139,75 | 0,65∙225=146,25 |
| Диаметр диска d | 406,4 | 406,4 (одинаковый с заводским) |
| Диаметр колеса D | 685,9 | 2∙146,25+406,4=698,9 |
| Длина окружности l=πD | 685,9π | 698,9π |
Итак, имеем две длины окружности, теперь надо найти, на сколько процентов увеличится пробег автомобиля при одном обороте колеса.
Заводское колесо 685,9π – 100%
Колесо на замену 698,9π – х %
Найдем значение х, используя правило пропорции: 698,9π ∙100685,9π=101,895…При решении числа π сократились, а значение % будет приближенное. Теперь найдем разницу между длинами окружностей 100% — 101, 895%=1,895%, округлим его, как сказано в условии – до десятых, получим 1,9 %. Наш ответ 1,9%.
Ответ: 1,9%
Общие советы и рекомендации по данному виду задач
Главное, с чем мы работаем в условии данной задачи, это маркировка шины.
Помните о том, что высота колеса – это его диаметр, состоящий из двух высот и одного диаметра диска (внутренняя металлическая часть колеса). Формулой D=2H+d придется пользоваться на протяжении нескольких заданий.
Для нахождения высоты переводим второе число маркировки в десятичную дробь (разделив на 100) и умножить его на первое число.
Используйте для решения таблицу, чтобы не запутаться при нахождении каких-либо данных.
Желаем удачи!
Ответ: см. решениеpазбирался: Алла Василевская | обсудить разбор
Задание 15MO04 (тарифы на мобильную связь)
На графике точками изображено количество минут, потраченных на исходящие вызовы, и количество гигабайтов мобильного интернета, израсходованных абонентом в процессе пользования смартфоном за каждый месяц 2018 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
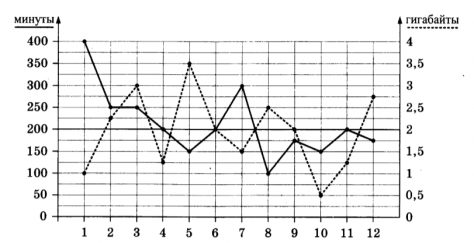
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составила 200 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа входит:
- пакет минут, включающий 200 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
- пакет интернета, включающий 2 гигабайта мобильного интернета;
- пакет СМС, включающий 90 СМС в месяц;
безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета указана в таблице:
|
Исходящие вызовы |
2 рубля/минута |
|
Мобильный интернет: дополнительные пакеты по 0,5 Гб |
150 рублей за пакет |
|
СМС |
2 рубля/штука |
Абонент не пользовался услугами связи в роуминге и не звонил на номера, зарегистрированные за рубежом. За весь год абонент отправил 50 СМС.
Задание №1. Определите, какие месяцы соответствуют указанному в таблице количеству израсходованных гигабайтов.
| Израсходованные гигабайты | 2,5 Гб | 1,5 Гб | 3,5 Гб | 1 Гб |
| Номер месяца |
Заполните таблицу, в ответ запишите подряд числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев июнь, сентябрь, ноябрь и декабрь в ответ нужно записать число 691112).
Решение
Рассматривая график, мы видим, что израсходованные гигабайты соединены пунктиром и получена ломаная линия. Чтобы найти, в каком месяце абонент израсходовал 2,5 Гб, надо от числа 2,5, расположенного на вертикальной оси справа, провести линию до пересечения с точкой на пунктирной ломаной. «Встреча» с точкой произойдет напротив числа 8, которое обозначает август месяц. Так проделываем с каждым заданным в таблице числом. Этот поиск чисел выделен разными цветами на графике ниже.
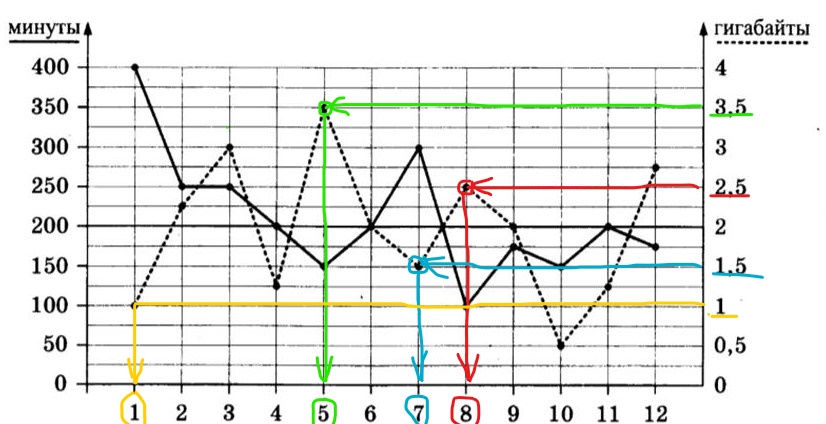
Таким образом, в таблицу 1 задания мы должны вписать числа, соответствующие месяцам:
| Израсходованные гигабайты | 2,5 Гб | 1,5 Гб | 3,5 Гб | 1 Гб |
| Номер месяца | 8 | 7 | 5 | 1 |
Ответ: 8751
Задание №2. Сколько рублей потратил абонент на услуги связи в феврале?
Решение
Для ответа на данный вопрос необходимо найти на графике февраль (месяц 2) и определить все виды переплат, если таковые были.
По условию задачи абонент может использовать 200 минут исходящих и 2 Гб интернета, это всё входит в его абонентскую плату 200 рублей (на графике в условии это жирная черная линия, она будет нашим ориентиром).
Выделим на графике февраль, затем точки этого месяца, которые показывают количество минут и количество Гб.
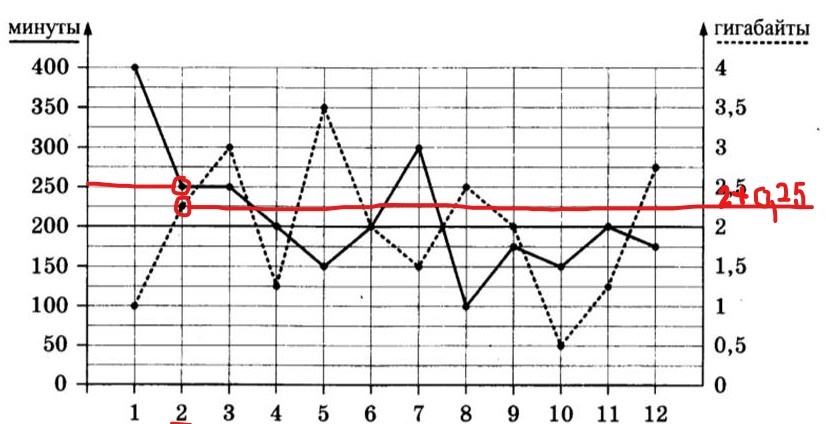
1)Определим «лишнее» количество исходящих минут. Горизонтальная, выделенная жирным линия, показывает тарифный план абонента. Всё, что выше этой линии, это за дополнительную плату. На столбце слева видно, что вместо 200 минут, он потратил 250 минут, значит, 50 минут у него сверх тарифа. Знаем по условию, что каждая дополнительная минута стоит 2 рубля, находим, что он заплатит за 50 минут 100 рублей: 2руб×50 мин=100 руб.
2) Теперь находим, какое количество Гб абонент истратил сверх тарифа. Справа на вертикальной линии показано, что абонент сверх тарифа истратил 0,25 Гб (по шкале слева видно, что 1 деление – это 0,25 Гб, так как это половина от 0,5 Гб). По условию знаем, что сверх тарифа пакеты по 0,5 Гб продаются по цене 150 руб/пакет. Также надо понимать, что меньше пакета нам не продадут, поэтому для 0,25 Гб нам надо купить 1 полный пакет стоимостью 150 рублей.
3) Каждый месяц абонент оплачивает фиксированную стоимость тарифа, это 200 рублей.
После того, как мы знаем, что в феврале переплата за звонки 100 руб, переплата за гигабайты 150 руб, абонентская плата 200 руб, найдем сколько рублей потрачено на услуги связи в феврале: 100+150+200=450 рублей.
Ответ: 450
Задание №3. Сколько месяцев в 2018 году абонент не превышал лимит по пакету исходящих минут?
Решение
Работаем с графиком. Надо определить, сколько месяцев НЕ превышал, то есть звонки были на уровне 200 минут или ниже. На графике такие звонки (точки на жирной линии) выделены красным цветом. Это были такие месяцы: апрель, май, июнь, август, сентябрь, октябрь, ноябрь, декабрь. Получилось, что 8 месяцев абонент не превышал лимит по пакету исходящих вызовов.
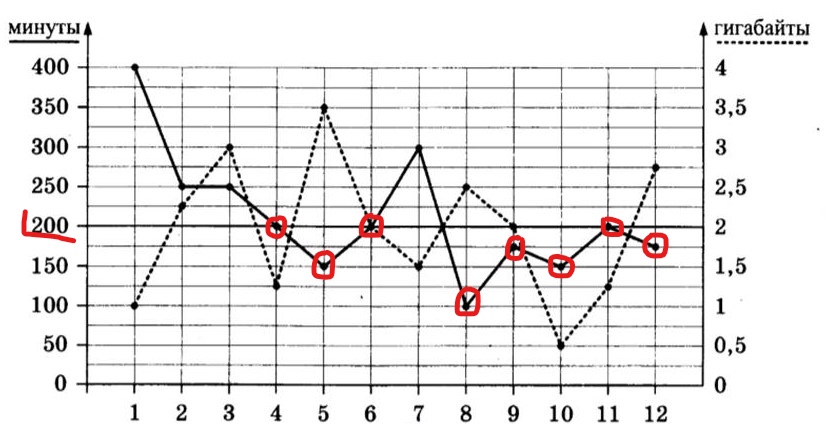
Ответ: 8
Задание №4. Сколько месяцев в 2018 году абонент не превышал лимит ни по пакету минут, ни по пакету мобильного интернета?
Решение
Работаем с графиком. Надо определить, сколько месяцев НЕ превышал по двум видам связи – звонки и интернет одновременно, то есть звонки были на уровне 200 минут или ниже, интернет на уровне 2Гб или ниже.
На графике такие минуты и гигабайты выделены красным цветом.
Это были такие месяцы: апрель, июнь, сентябрь, октябрь, ноябрь. Получилось, что 5 месяцев абонент не превышал лимит ни по пакету исходящих вызовов, ни по пакету мобильного интернета.
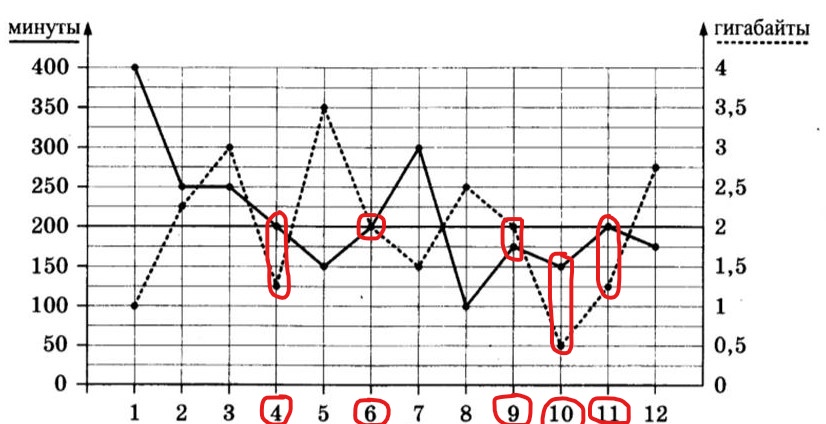
Ответ: 5
Задание №5. В конце 2018 года оператор связи предложил абоненту перейти на новый тариф, условия которого приведены в таблице.
|
Стоимость перехода на тариф |
0 руб |
|
Абонентская плата в месяц |
350 руб |
|
В абонентскую плату ежемесячно включены: |
|
|
Пакет исходящих минут |
300 минут |
|
Пакет мобильного интернета |
3,5 Гб |
|
Пакет СМС |
80 СМС |
|
После расходования пакетов: |
|
|
Входящие вызовы |
0 руб |
|
Исходящие вызовы* |
1,5 руб/минута |
|
Мобильный интернет: дополнительные пакеты по 0,5 Гб |
110 руб за пакет |
|
СМС |
3 руб/штука |
*исходящие вызовы на номера, зарегистрированные в РФ
Абонент решает, перейти ли ему на новый тариф, посчитав, сколько бы он потратил на услуги связи за 2018 г, если бы пользовался им. Если получится меньше, чем он потратил фактически за 2018 г, то абонент примет решение сменить тариф.
Перейдет ли абонент на новый тариф? В ответе запишите ежемесячную плату по тарифу, который абонент выберет на 2019 год.
Решение
Условие 5 задания нам покажется большим, но суть его состоит в том, чтобы определить, перейдет абонент на новый тариф или нет. Для этого надо сравнить старый и новый тарифы, просчитав плату по ним по графику 2018 года.
Тариф «Стандартный» (назовем его старый тариф). Знаем, что абонент ежемесячно платит за него 200 руб. Таким образом, в год он оплачивает по пакету 200 руб×12 месяцев=2400 рублей.
Кроме этого, абонент иногда покупал дополнительные минуты и пакеты интернета. Их нам предстоит обсчитать.
Начнем с минут, работа идет по графику. Красными столбцами показано количество минут, за которые идет дополнительная плата, наверху такого столбца написано, сколько минут было куплено дополнительно (разница между 200 минутами по тарифу и фактическим числом минут).
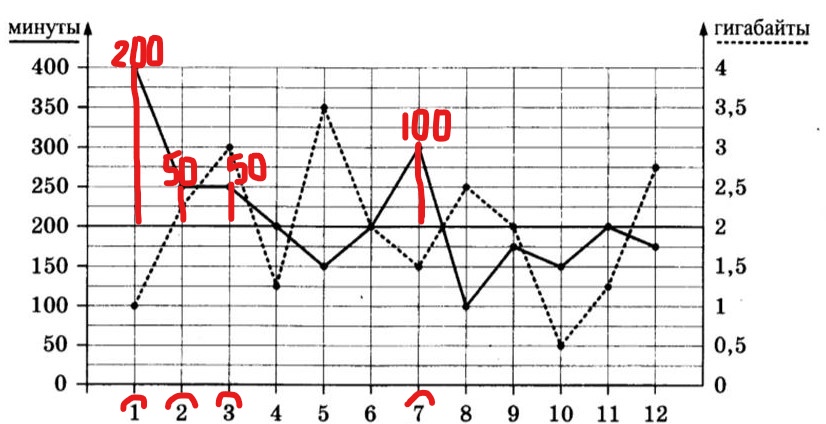
Теперь сложим все дополнительные минуты: 200+50+50+100, получим 400 минут. Знаем по условию, что 1 дополнительная минута старого тарифа стоит 2 рубля, умножим 400 на 2, получим 800 рублей.
Итак, 800 рублей — это оплата за дополнительные минуты сверх пакета.
Аналогично обсчитаем мобильный интернет, выделяя на графике дополнительно купленные пакеты.

Помним, что 1 пакет – это 0,5 Гб, на графике это 2 деления. Обводим месяцы, в которых ему пришлось купить дополнительные пакеты: февраль, март, май, август, декабрь. Подписываем над каждым столбцом, сколько пакетов ему пришлось купить (помним, что неполный пакет не продадут). Теперь складываем количество купленных пакетов за год: 1+2+3+1+2, подучается, что он купил 9 пакетов, каждый из которых стоил 150 рублей (сказано в условии).
Значит надо: 150 руб×9 пак.=1350 рублей его переплата за мобильный интернет.
Теперь надо сложить все полученные за год суммы: 2400 руб (аб.плата)+800 руб (минуты)+1350 руб(за ГБ). Получится сумма 4550 руб. Столько абонент потратил за 2018 год по тарифу «Стандартный».
Теперь необходимо провести аналогичные операции по расчетам оплаты по новому тарифу, который предложили абоненту.
Итак, его ежемесячная абонентская плата составит 350 рублей, следовательно за 12 месяцев он заплатит 350 руб×12 мес=4200 рублей.
Теперь надо рассмотреть по графику, потребовались бы ему по новому тарифу дополнительные минуты или пакеты интернета. Помним, что в новый тариф входит 300 минут и 3,5 Гб мобильного интернета.
Начнем рассматривать с минут. Проведем новую линию на графике от левого столбца (минуты), теперь она наш ориентир. Теперь видно, что дополнительные минуты требуются только в январе, их количество – 100.
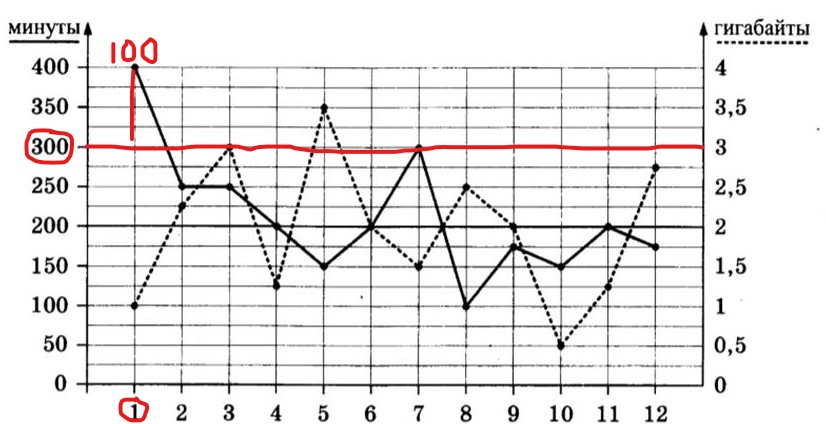
Значит, дополнительные 100 минут требуются только в январе. Рассчитаем их стоимость, зная по условию 5 задания, что дополнительная минута стоит 1,5 рубля: 1,5 руб×100 минут=150 рублей.
Теперь необходимо определить, понадобились бы ему дополнительные пакеты интернета. По условию теперь 3,5 Гб входит в абонентскую плату. Поработаем с графиком. Проведем линию от 3,5 Гб (на оси слева), теперь она наш новый ориентир. Глядя на него, видно, что дополнительные гигабайты ему не понадобились.
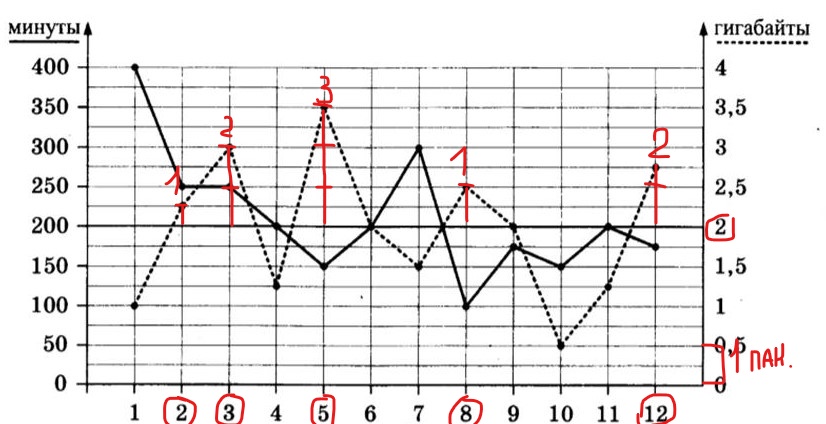
Теперь надо сложить все полученные за год суммы: 4200 руб (аб.плата)+150 руб (минуты). Получится сумма 4350 руб. Столько абонент потратил бы за 2018 год по новому тарифу, который ему предложили.
Теперь сравниваем годовую стоимость по двум тарифам:
«Стандартный» — 4550 руб, новый – 4350 руб. Получается, что по новому тарифу оплата дешевле. Значит, абонент перейдет на новый тариф.
Обратим внимание на то, что требуется записать в ответ: «В ответе запишите ежемесячную плату по тарифу, который абонент выберет на 2019 год». Так как абонент выбрал новый тариф, абонентская плата по которому 350 рублей, то и в ответ мы запишем число 350.
Ответ: 350
Общие советы и рекомендации по данному виду задач:
- Не нужно бояться большого условия. Мы все пользуемся мобильной связью, оплачиваем иногда дополнительные минуты и гигабайты, но не задумываемся над расчетами, а именно их мы будем выполнять. Это может пригодиться нам в жизни.
- При чтении задачи выделяйте главное – стоимость основного пакета и что в него входит, а затем всё, что покупается сверх пакета и стоимость.
- Помним, что на графике минуты – это черная жирная линия, а гигабайты – это пунктир. Работать надо только с жирными точками, стоящими на этих линиях.
- Помним, что пакеты интернета не делятся на части, их не продают «по кусочкам», как минуты.
- Выполняя расчеты за месяц или за год, не забываем про ежемесячную абонентскую плату.
- Перед тем, как записать ответ к заданию, еще раз внимательно прочитайте, что именно требуется записать.
pазбирался: Алла Василевская | обсудить разбор
Задание 15МО3 (земледельческие террасы)
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы. Земледельческие террасы – это горизонтальные площадки, напоминающие ступени. Во время дождя стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье – для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует большого ручного труда.

Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 30 м, а верхняя точка находится на высоте 5 м от подножия.
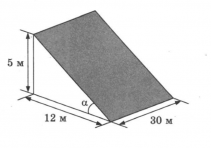
Задание №1. Земледелец на расчищенном склоне холма выращивает мускатный орех. Какова площадь, отведенная под посевы? Ответ дайте в квадратных метрах.
Решение
Мускатный орех земледелец выращивает на склоне холма. Если смотреть на геометрический рисунок, где 5 метров – это высота холма, 30 метров – ширина участка, а 12 метров – это расстояние от подножия холма до нижней точки уклона. Таким образом, расчищенным склоном холма является прямоугольник, закрашенный на рисунке серым цветом.
Требуется найти площадь этого прямоугольника. Смотрим, что его ширина 30 м, а длина неизвестна, но она является гипотенузой прямоугольного треугольника с катетами 5 и 12 метров.
Гипотенузу найдем по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов). Обозначим гипотенузу буквой с и запишем ее нахождение: с2=122+52=144+25=169; так как √169=13, то с=13.
Теперь находим площадь расчищенного склона холма. Для нахождения S прямоугольника надо длину умножить на ширину. То есть имеем, что 13 м – это длина участка, а 30 м – ширина участка, значит S=13∙30=390 м2
В ответ запишем число 390 (наименования в бланк не пишем).
Ответ: 390
Задание №2. Земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона а, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.
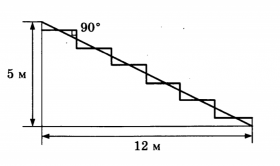
Решение
Во-первых, найдем тангенс по рисунку, который нам дан. Вспомним, что тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Поэтому, в нашем случае это отношение 5 к 12, то есть tq a=512. Умножим это число на 100%, как сказано в условии задачи, и посчитаем: 512×100=41, 666… Нам сказано, что необходимо округлить число до десятых, то есть оставить после запятой одну цифру (десятые доли), применив правило округления. Получим: 41, 666..≈41,7. Мы видим, что угол склона холма не превышает 50%, то есть он удовлетворяет требованиям для строительства террас. Значит, наш ответ 41,7%.
Ответ: 41,7
Задание №3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
Решение:
Для ответа на вопрос задания необходимо сравнить две площади – посевную площадь до строительства террас и площадь террас.
Посевная площадь у нас найдена в задании №1, она равна 390 м2.
Требуется найти площадь террас. Надо понять, что она собой представляет. Посмотрим внимательно на рисунок, где изображены террасы («ступеньки» можно их назвать, глядя на рисунок). Если каждую такую «ступеньку» опустить вниз, то они как раз войдут в расстояние 12 м, то есть длина всех террас, отведённых под посевы равна 12 метров. Ширина участка нам известна, она равна 30 метров. Таким образом, мы получили прямоугольник со сторонами 12 и 30 метров, значит, найдем его площадь, что и будет являться площадью террас: 12×30=360 м2.
Вот теперь мы видим, что сначала площадь была 390, а затем она немного уменьшилась и стала равна 360 м2.
Осталось сравнить процентное отношение данных площадей.
Это можно сделать двумя способами.
1 способ: запишем условие для решения, помня, что первоначальная площадь равна 100%.
390 м2 – 100%
360 м2 – х%
Найдем, сколько процентов стала площадь террас: х= 360×100:390=92,307… Так как нам сказано в условии, что ответ надо будет округлить до десятых, то можно это сделать с числом 92,307…: 92,307≈92,3. Помним, что это мы нашли, сколько процентов стала площадь террас. Теперь находим разницу между ними: 100% — 92,3%=7,7%. Её и запишем в ответ.
2 способ: можно решить данную задачу другим способом, имея две площади – 390 м2 и 360 м2. Видим, что площадь уменьшилась на 30 м2, так как 390 – 360 =30.
Значит: 390 м2 – 100%, а 30 м2 — х%. Следовательно х=30×100:390=7,69…%. Округлим до десятых наше число и получим 7,7.
Ответ: 7,7
Задание №4. Земледелец получает 800 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 22% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
Решение:
Смысл данной задачи в том, что земледелец выращивает на террасах бурый рис, затем его обрабатывает и получает белый рис. При обработке масса теряется. Нам надо узнать, сколько кг белого риса он получит со своего участка.
Помним, что рис собирают с террас, площадь которых 360 м2 (мы нашли её в задании 3). Известно, что с 1 м2 собирают 800 г бурого риса, следовательно, чтобы найти, сколько бурого риса он соберет со всего участка площадью 360 м2, надо 800×360, получим 288000 граммов. Переведем граммы в килограммы (это требуется в данной задаче), то есть разделим на 1000, так как 1 кг=1000 г. Значит, 288000:1000=288 кг собирает земледелец бурого риса.
Теперь он его обрабатывает, теряя 22%, значит, из данной массы 288 кг мы должны убрать 22%. Так как 288 кг – это 100%, то после обработки остается 100% — 22%=78%. Переведем 78% в десятичную дробь, получим 0,78. Теперь умножим на 0,78 наши 288 кг, получаем 224,64 кг.
Ответ: 224,64
Задание №5. В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая – летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Рис | Кукуруза | Пшено | |
| 1-ый урожай (июнь) | 600 г/м2 | 1200 г/м2 | Не выращивают |
| 2-ой урожай (сентябрь) | 800 г/м2 | Не выращивают | 300 г/м2 |
Решение:
Итак, подчеркнем в условии для себя, что нам надо найти: В таблице дана урожайность культур, которые может засеять земледелец на своем террасированном участке. За год обычно собирают два урожая – летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
Наибольшее число килограммов урожая летом – это урожай кукурузы, а осенью – урожай риса. Выделим это в таблице:
| Рис | Кукуруза | Пшено | |
| 1-ый урожай (июнь) | 600 г/м2 | 1200 г/м2 | Не выращивают |
| 2-ой урожай (сентябрь) | 800 г/м2 | Не выращивают | 300 г/м2 |
Складываем эти два числа: 1200+800=2000 г/м2, получаем количество урожая с 1 квадратного метра в граммах. Знаем, что площадь террас равна 360 м2 (мы нашли её в задании номер 3). Значит, надо 2000 умножить на 360, получим: 2000×360=720000 г/м2. Теперь переведем наше число в килограммы, так как это требуется по условию задачи: 720000 г = 720 кг (знаем, что 1 кг=1000 г, поэтому разделили на 1000, убрав три нуля). Наш ответ 720 кг
Ответ: 720
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 15МО1 (дачный участок)
На плане изображен загородный дачный участок садоводства «Товарищество», Улица Виноградная, 45. (Сторона каждой клетки на плане равна 2м) Участок имеет прямоугольную форму. Въезд и выезд осуществляется через единственные ворота. При въезде на участок слева от ворот находится гараж, а справа – баня, отмеченная цифрой 4.
Площадь, занятая гаражом, равна 60 кв.м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеются квадратный бассейн, расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Справа от жилого дома имеются посадки фруктовых деревьев: яблоневых, вишневых, абрикосовых, грушевых.
Перед жилым домом и рядом с баней разбиты клумбы с цветами. Перед домом растут розы, а рядом с баней – гладиолусы. Перед гаражом имеется площадка, вымощенная резиновой плиткой размером 2м˟2м. Все дорожки внутри участка имеют ширину 2м и вымощены такой же плиткой.
К домохозяйству подведены электричество и вода. Имеется магистральное газоснабжение.
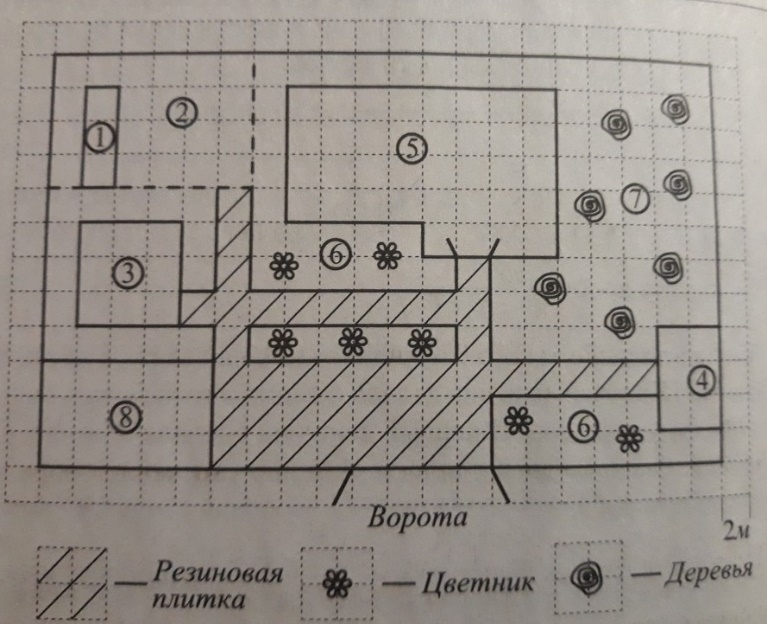
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность четырех цифр.
| Объекты | Жилой дом | Бассейн | Гараж | Теплица |
| Цифры |
Для того, чтобы правильно определить номера объектов, необходимо при чтении информации выделять (почеркивать) их как в тексте, так и сразу же подписывать в план-схеме. Ниже показана часть текста, в которой подчеркнуты основные моменты.
При въезде на участок слева от ворот находится гараж, а справа – баня, отмеченная цифрой 4.
Площадь, занятая гаражом, равна 60 кв.м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеются квадратный бассейн, расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Справа от жилого дома имеются посадки фруктовых деревьев: яблоневых, вишневых, абрикосовых, грушевых. Перед жилым домом и рядом с баней разбиты клумбы с цветами. Перед домом растут розы, а рядом с баней – гладиолусы.
Все эти объекты подписываем на схеме. Таким образом, получаем:
- Теплица
- Огород
- Бассейн
- Баня
- Дом
- Клумба с гладиолусами
- Деревья
- Гараж
Теперь расставляем номера необходимых объектов в таблицу:
| Объекты | Жилой дом | Бассейн | Гараж | Теплица |
| Цифры | 5 | 3 | 8 | 1 |
В бланк записываем ответ: 5381
Задание №2
Резиновая плитка продается в упаковках по 4 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку перед гаражом?
Решение: для того, чтобы узнать, какое количество упаковок нужно купить, надо посчитать количество резиновых плиток на схеме. Под схемой показано, как она обозначена. Это количество небольшое, поэтому просто считаем клеточки на схеме. Отметим их красной звездочкой.
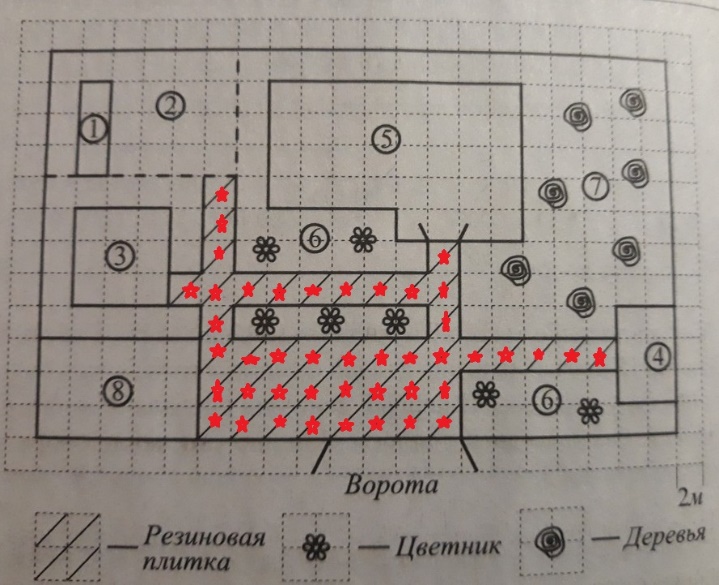
В данном случае их 44. Зная, что в 1 упаковке их 4 штуки, разделим 44 на 4 и получим 11 упаковок. Значит, наш ответ 11. Записываем его в бланк.
Задание №3
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Решение: дом – это объект под номером 5. Для нахождения площади нам необходимо знать сторону каждой клетки на плане. Это указано в первом абзаце текста. Подчеркнем это место.
На плане изображен загородный дачный участок садоводства «Товарищество», Улица Виноградная, 45. (Сторона каждой клетки на плане равна 2м)
Если сторона одной клетки 2 метра, то ее площадь 2*2=4 квадратных метра. Считаем количество клеток в доме и умножаем его на 4.
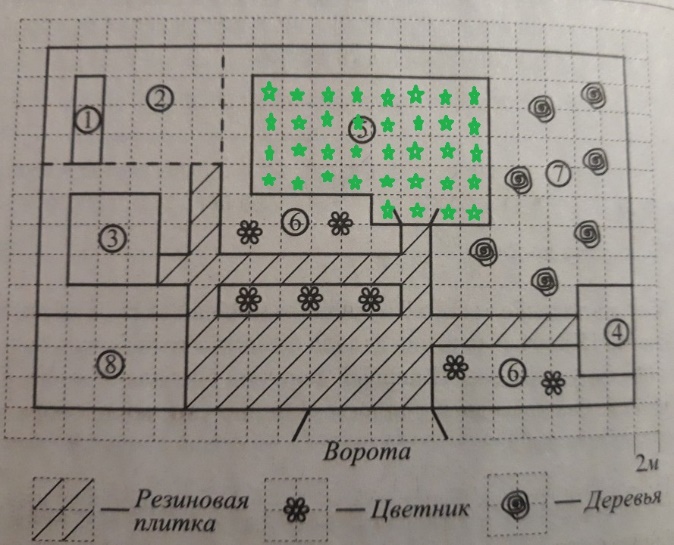
Количество клеток равно 36 (отмечены зелеными звездочками). Умножаем 36 на 4, получаем 144. Значит 144 квадратных метра – площадь дома. Записываем ответ 144 в бланк.
Задание №4
Найдите наименьшее расстояние (в метрах) от жилого дома до входных ворот.
Решение: наименьшее расстояние – это всегда прямо от одного объекта до другого. Считаем количество клеток от объекта 5 до ворот, их 6 (выделены синими звездами).
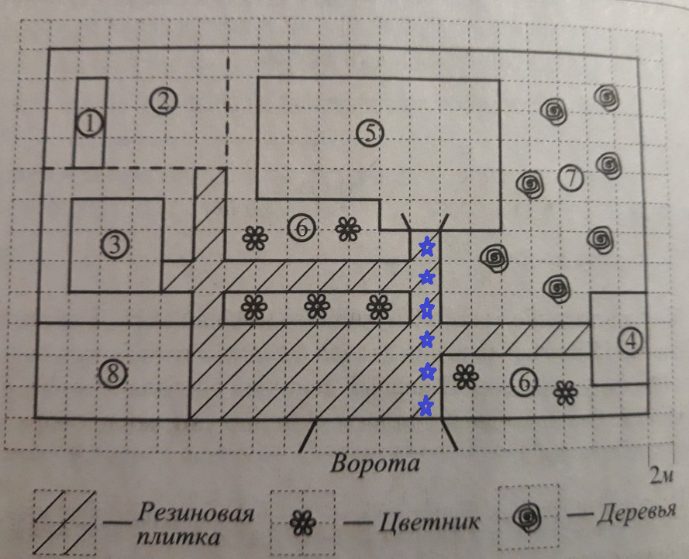
Помним, что сторона клетки по условию – 2 метра, значит, 6 умножаем на 2 и получаем 12 метров. В бланк записываем число 12.
Задание №5
Хозяин планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: газовое или электрическое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимость даны в таблице.
| Нагреватель (котел) | Прочее оборудование и монтаж | Средний расход газа/средняя потребляемая мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 25 тыс. руб | 20 000 руб. | 1,4 куб. м/ч | 4,5 руб./куб.м |
| Электр. отопление | 22 тыс. руб | 16 520 руб. | 5,5 кВт | 3,6 руб./(кВт.ч) |
Обдумав оба варианта, хозяин решал установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Решение: для решения этого задания необходимы данные только из таблицы. Рассматриваем сначала стоимость каждого оборудования в отдельности:
25 000 + 20 000 = 45 000 рублей – стоит оборудование для газового отопления
22 000 + 16520 = 38 520 рублей – стоит оборудование для электрического отопления
Теперь находим разницу в стоимости, так как в вопросе конкретно указано, что это надо найти: компенсирует разность в стоимости установки газового и электрического отопления.
45000 – 38520 = 6480 рублей разница в стоимости установки
Дальше высчитываем стоимость потребления газа и электричества по указанным в таблице данным:
1,4 умножаем на 4,5 и получаем 6,3 рубля — стоимость потребления газа в час
5,5 умножаем на 3,6 и получаем 19,8 рублей – стоимость потребления электроэнергии в час
Теперь также находим разницу в стоимости между ними, то есть сколько сэкономит хозяин при установке газового оборудования: 19.8 – 6,3= 13,5 рублей.
Чтобы ответить на главный вопрос задания — Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Нужно разницу в стоимости установки разделить на разницу в стоимости потребления:
6480:13,5=480 часов.
Записываем в ответ число 480.
Ответ: см. в решенииpазбирался: Базанов Даниил | обсудить разбор
Задание 15МО2 (схема метро)
На рисунке изображена схема метро в городе N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Веселая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная. Всего в метрополитене города N есть три станции, от которых тоннель ведет только в одну сторону – это станции Дальняя, Верхняя и Звездная. Максим живет недалеко от станции Надежда.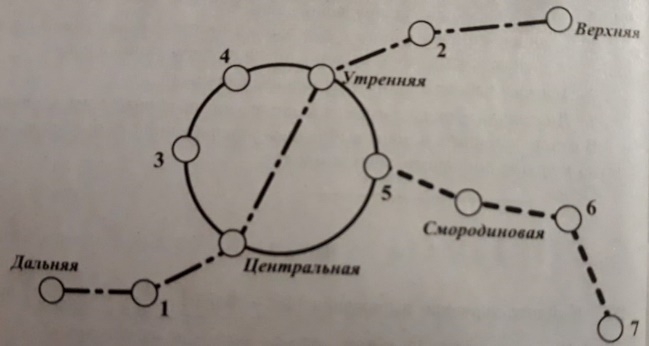
Задание №1
Для станций, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность четырех цифр.
| Станции | Хоккейная | Надежда | Птичья | Ветреная |
| Цифры |
Решение: для того, чтобы правильно определить номера станций, необходимо при чтении информации выделять (подчеркивать) их как в тексте, так и сразу же подписывать на рисунке. Ниже показана часть текста, в которой подчеркнуты основные моменты, а также расстановка станций, которая выполняется сразу по ходу чтения текста.
Станция Ветреная расположена между станциями Центральная и Дальняя (значит, это номер 1). Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя (сразу видно, что двигаться надо от Центральной к Утренней, значит, Быстрая будет под номером 5), Птичья и Веселая (соответственно 4 и 3, так как двигаемся по кольцу). Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная (видим эту ветку справа нижнюю, соответственно Хоккейная – номер 6, а Звездная – 7). Максим живет недалеко от станции Надежда (она под номером 2, так как осталась одна не указанная).
Теперь расставляем номера необходимых объектов в таблицу:
| Станции | Хоккейная | Надежда | Птичья | Ветреная |
| Цифры | 6 | 2 | 4 | 1 |
В бланк записываем ответ: 6241
Задание №2
Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяженностью 8 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 500 метров. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Решение: для того, чтобы узнать, сколько дней был закрыт проезд, нужно узнать, сколько рабочих дней они прокладывали рельсы. По условию длина участка 8 км, переводим ее в метры, так как в 1 день меняли по 500 метров. Получаем 8000 метров. Теперь делим 8000 метров на 500 метров, получаем 16 рабочих дней трудилась бригада. Нам надо узнать, сколько дней всего был закрыт проезд, так как в выходные работ не было, а проезд был закрыт. По условию работы начались с понедельника, значит бригада работала 3 полных недели и 1 понедельник на четвертой неделе (16 дней делим на 5 рабочих в неделю, получается 3 недели и 1 остается – понедельник). После каждой недели у нас два дня выходных: 2 после первой, 2 после второй, 2 после третьей. Таким образом, 6 выходных был закрыт проезд. Значит, 16 рабочих и 6 выходных, это 22 полных дня был закрыт проезд.
Записываем ответ 22 в бланк.
Задание №3
Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S (в квадратных километрах), если длина кольцевой ветки равна 32 км. В ответе укажите S*.
Решение: так как известна длина кольцевой ветки, то это значит, что мы имеем длину окружности (по условию – кольцевая ветка – это окружность). Длина окружности вычисляется по формуле 2πR. Значит, 2πR=32. Делим обе части на 2, получаем πR=16. Находим радиус, для этого надо 16 разделить на число π. То есть R=16/π. Формула площади круга S=πR2. Подставляем в нее вместо радиуса 16/π. Получаем, что S=π(16/π) 2. Возводим в квадрат, получаем S=π(256/π2). Теперь сокращаем числитель и знаменательна число π. Получается, что S=256/π . Поскольку в задании есть указание, что в ответ надо записать S* , то умножая эти величины в нашей формуле S=256/π, получаем, что S*= 256. Записываем ответ 256 в бланк.
Задание №4
Найдите расстояние (по железной дороге) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 14 км, расстояние от Звездной до Смородиновой 11 км, а от Быстрой до Хоккейной – 7 км. Все расстояния даны по железной дороге.
Решение: итак, Радужная ветка – это станции Быстрая, Смородиновая, Хоккейная и Звездная. Можно для удобства сделать чертеж и обозначить на нем станции первыми буквами их названий и расставить длины. Получится вот такой рисунок, по которому можно легко определить расстояние от Смородиновой (С) до Хоккейной (Х).
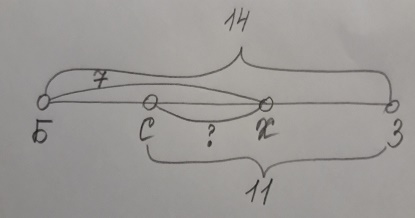
Для этого из длины отрезка СЗ=11 нужно вычесть длину отрезка БХ=7, получим длину СХ=4. В бланк записываем число 4.
Задание №5
Школьник Максим в среднем за месяц совершает 45 поездок на метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Максим уедет из города к бабушке в деревню и неиспользованные карточки обнулятся. Во сколько рублей обойдется самый дешевый вариант?
| Количество поездок | Стоимость одной поездки
(в рублях) |
Дополнительные условия |
| 1 | 40 | Школьникам скидка 20% |
| 10 | 37 | Школьникам скидка 10% |
| 30 | 35 | Школьникам скидка 10% |
| 50 | 32 | Нет |
| Безлимит | — | Любое число поездок в течение месяца за 2000 рублей |
Решение: для решения этого задания необходимы данные только из таблицы. Итак, нужно совершить 45 поездок за наименьшую стоимость. Значит, два последних варианта не подходят, так как 50 поездок – это много, деньги на карте обнулятся, а по Безлимиту в среднем приблизительно выйдет одна поездка 44 рубля (2000 : 45 поездок), скидки здесь не предусмотрены. Следовательно, будем составлять наборы из первых трех вариантов, а затем выбирать самый дешевый.
Для удобства надо посчитать каждый из трех вариантов, как карточку для школьника, т.е. с указанной скидкой. Затем посчитать стоимость каждой карточки полностью. Вспомним, чтобы найти количество процентов от данного числа, надо число разделить на 100 и умножить на количество процентов. Запишем это решение в таблице.
| Количество поездок | Стоимость одной поездки
(в рублях) |
Стоимость одной поездки для школьника
(в рублях) |
Стоимость 1 карточки для школьника
(в рублях) |
| 1 | 40 | 40-40:100*20=32 | 1*32=32 |
| 10 | 37 | 37-37:100*10=33,3 | 10*33,3=333 |
| 30 | 35 | 35-35:100*10=31,5 | 30*35=945 |
- Допустим, что можно купить из первого варианта 45 карточек по 32 руб. Тогда получим, что 32*45=1440 руб.
- Допустим, что можно купить на 45 поездок: одну третью (на 30 поездок), 1 вторую (на 10 поездок) и пять первых (на пять поездок). Рассчитаем стоимость.
Одна третья карточка на 30 поездок – это 945 рублей.
Одна вторая карточка на 10 поездок – это 333 рубля.
Пять первых карточек: 32*5=160 рублей.
Теперь складываем стоимость всех карточек. 945+333+160=1438 рублей. Это уже меньше, чем в решении 1.
- Допустим, что можно купить 1 третью карточку (на 30 поездок) и 15 первых, так как это тоже 45 поездок. Одна третья карточка на 30 поездок – это 945 рублей. 15 первых будут стоить 15*32=480 рублей. Складываем стоимости 945 и 480, получаем 1425 рублей.
- Допустим, что можно еще купить 4 вторых (на 40 поездок) и 5 первых карточек. Тогда 4*333=1332 руб; 5*32=160 руб. Вместе это составит 1332+160=1492 рубля.
Записываем в ответ число 1425, так как это самый дешевый вариант из всех.
Ответ: см. в решенииpазбирался: Базанов Даниил | обсудить разбор
👀 125k
Спасибо. Думаю,что детям понятно. Нельзя ли рассмотреть вариант задачи с шинами?
Тоже интересует такой вопрос, задачи про шины!
Да нельзя ли с шинами?
Вряд ли,я сама в 9 классе, учитель сказал что все можно нарешать,но спасибо и на этом,продолжайте в том же духе
Про печки посмотрел всё понял
Все понятно объяснено, спасибо
не очень понятны задания про зонт
было сложно, но через некоторое время я уже немного понял
3,4 Задания про печь, непонятны мне
Извиняюсь, случаино ответила вам
В задаче про печку,не понятно 4 задание
Задания 3,4 про печь
Непонятны
В задаче про печь, не понятно 2 задание
Всё понятно. кроме 5 задачи про печки
5 задание не понятное
в заданиях про печку не поняла 5 номер
не смог немного но разбераюсь 2 и еще пару штука
НЕ смог 4тое
Будем разбирать еще
Вроде бы все понятно, но есть затруднения в 5 задании
про печки задачи прочитала, всё поняла
Про печки, всё понял
Хорошо)
все понятно.!
поняла про печь, 4 и 5 задание не поняла
задачи про шины. не поняла 2 и 3 задание