Задание №29 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Особенность задания № 29 заключается в том, что в нем требуется использование материалов не менее чем из двух-трех разделов механики. Актуальные сведения, необходимые для решения задания, приведены в разделе теории. Законы сохранения, силы, действующие в макромире, и другая нужная информация содержится в разделах теории соответствующих типовых заданий по механике.
Задание ЕГЭ-Ф-ДВ2023-29
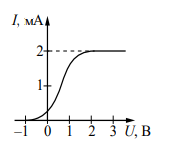 В опыте по изучению фотоэффекта монохроматическое излучение мощностью Р = 0,21 Вт падает на поверхность катода, в результате чего в цепи возникает ток. График зависимости силы тока I от напряжения U между анодом и катодом приведён на рисунке. Какова частота ν падающего света, если
в среднем один из 30 фотонов, падающих на катод, выбивает электрон?
В опыте по изучению фотоэффекта монохроматическое излучение мощностью Р = 0,21 Вт падает на поверхность катода, в результате чего в цепи возникает ток. График зависимости силы тока I от напряжения U между анодом и катодом приведён на рисунке. Какова частота ν падающего света, если
в среднем один из 30 фотонов, падающих на катод, выбивает электрон?Алгоритм решения:
Решение:
Запишем исходные данные:
Сила тока — это заряд q, прошедший через поперечное сечение проводника за время t:
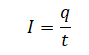
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока. Численно ток насыщения равен отношению суммарному заряду вырванных электронов в единицу времени:..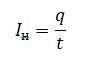
За время t через поперечное сечение проводника проходит заряд, равный произведению количества электронов, прошедших за время 1 с, единичному заряду электрона и времени t:
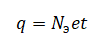
Но согласно условию количество электронов определяется формулой:
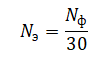
Следовательно, ток насыщения равен:
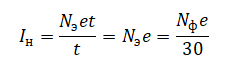
Энергия фотона определяется формулой:
![]()
Мощность монохроматического излучения равна суммарной энергии фотонов, падающих на поверхность катода в единицу времени:
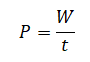
Суммарная энергия фотонов, падающих на поверхность катода за 1 секунду:
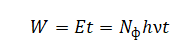
Тогда мощность равна:
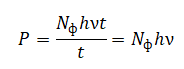
Количество фотонов можем выразить из формулы тока насыщения:
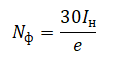
Следовательно, мощность равна:
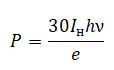
Отсюда частота падающего света равна:
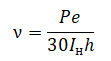
Ток насыщения смотрим по графику — он равен 2 мА, или 2∙10–3 А. Заряд электрона и постоянная Планка — константы.
Подставляем известные данные и делаем вычисления:
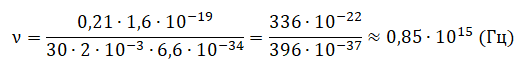
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18920
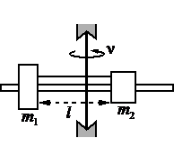 На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
Алгоритм решения
Решение
Запишем исходные данные, сразу переведя их в СИ:
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
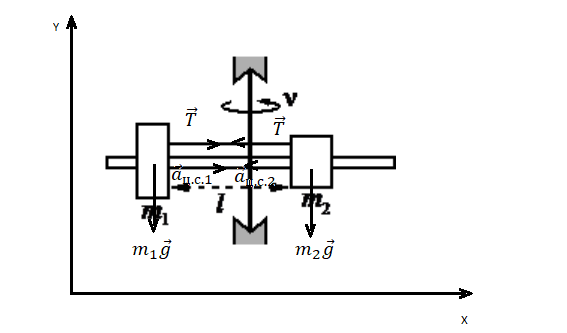
Запишем второй закон Ньютона для первого и второго груза соответственно:
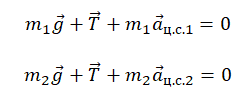
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
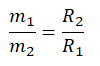
Подставим радиус второй окружности и выразим радиус первой окружности:
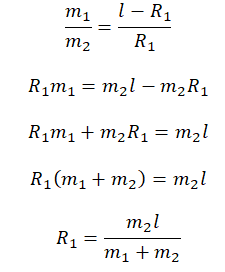
Следовательно, центростремительное ускорение первого груза равно:
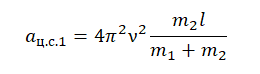
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
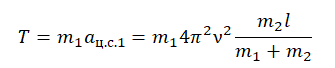
Подставим известные данные и вычислим силу натяжения нити:
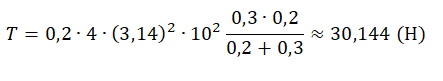
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18982
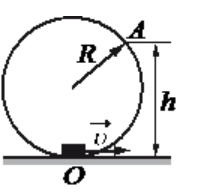 Небольшая шайба массой m=10 г, начав движение из нижней точки закреплённого вертикального гладкого кольца радиусом R=0,14 м, скользит по его внутренней поверхности. На высоте h=0,18 м она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? Сделайте рисунок с указанием сил, действующих на шайбу в точке А.
Небольшая шайба массой m=10 г, начав движение из нижней точки закреплённого вертикального гладкого кольца радиусом R=0,14 м, скользит по его внутренней поверхности. На высоте h=0,18 м она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? Сделайте рисунок с указанием сил, действующих на шайбу в точке А.
Алгоритм решения
Решение
Запишем исходные данные:
Сделаем чертеж. Выберем систему координат такую, чтобы направление линейной скорости шайбы в точке совпадала с направлением оси ОУ.
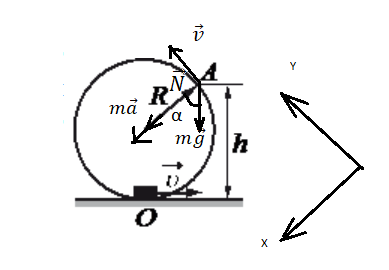
Запишем второй закон Ньютона в векторной форме:
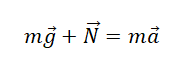
Под ускорением в этой записи понимается полное ускорение, составляющими которого является центростремительное и тангенциальное ускорение, направленное касательно к окружности (на рисунке мы его не обозначили, так как оно нам не понадобится).
Запишем проекцию на ось ОХ. Учтем, что в точке А шайба отрывается от кольца и падает. Следовательно, нормальная реакции опоры равна нулю:
mg cosα = maц.с.
Кинетическая энергия тела определяется формулой:
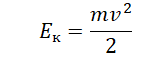
Выразим центростремительное ускорение из проекции на ось ОХ:
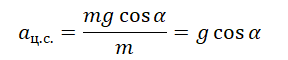
Но центростремительное ускорение также определяется формулой:
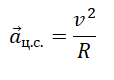
Приравняем правые части уравнений и получим:
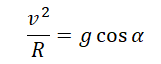
Квадрат скорости будет равен:
![]()
Следовательно, кинетическая энергия равна:
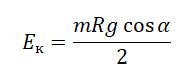
Чтобы избавиться от неизвестных величин, обратимся к геометрии:
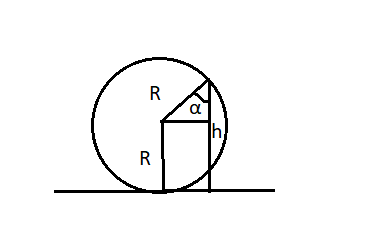
Из рисунка видно, что высота h есть сумма радиуса окружности и произведения радиуса на косинус угла α:
h = R + Rcosα
Отсюда следует, что:
Rcosα = h – R
Подставим это выражение в формулу кинетической энергии и выполним вычисления:
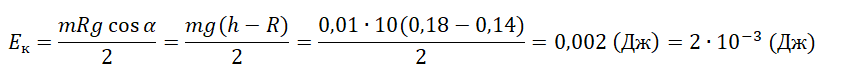
Отсюда следует, что кинетическая энергия шарика в начале движения равна 2 мДж.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Алгоритм решения
Решение
Запишем исходные данные:
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
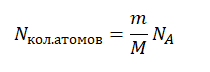
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
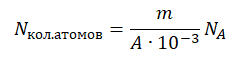
Энергия, выделенная всеми атомами, равна:
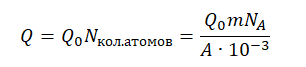
Теперь можем вычислить КПД:
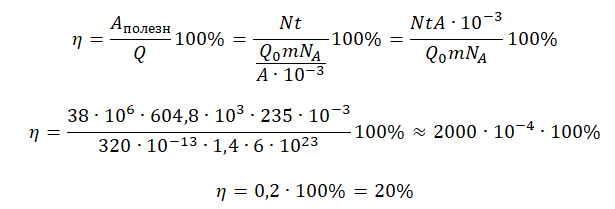
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17562
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18127
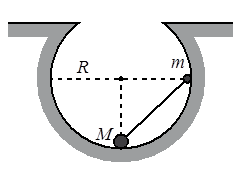 Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.
Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.
В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?
Алгоритм решения
Решение
Запишем исходные величины:
Переведем единицы измерения величин в СИ:
30 г = 0,03 кг
60 г = 0,06 кг
12 см = 0,12 м
Выполним чертеж:
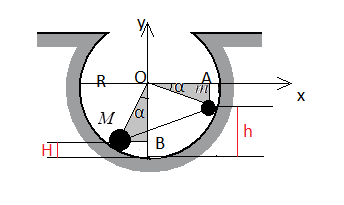
Нулевой уровень — нижняя точка выемки.
Запишем закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep = const
В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:
Ep0m = mgR
Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:
Epm = mgh
EpM = MgH
Поэтому закон сохранения энергии применительно к задаче примет вид:
mgR = mgh + MgH
Преобразуем выражение и получим:
mgR−mgh=MgH
R−h=MgHmg=MHm
При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:
MB = mA = R – h
OA = OB = R – H
OM = Om = R
Это дает нам право воспользоваться теоремой Пифагора:
(R−h)2=R2−OA2=R2−(R−H)2
Следовательно:
(R−h)2=R2−(R2−2RH+H2)=2RH−H2
Подставим в это выражение правую часть ранее полученного выражения:
R−h=MHm
(MHm)2=2RH−H2
Теперь можем выразить и вычислить радиус:
2RH=(MHm)2+H2
R=(MHm)2+H22H
R=(Mm)2H2+H2=(0,060,03)20,122+0,122=0,3 (м)
Ответ: 0,3
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18057
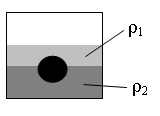 На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ1 = 400 кг/м3 и ρ2 = 2ρ1, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?
На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ1 = 400 кг/м3 и ρ2 = 2ρ1, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?
Алгоритм решения
Решение
Запишем исходные данные:
Построим рисунок и укажем все силы, действующие на шарик:
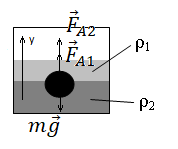
Запишем второй закон Ньютона в векторном виде:
m→g+→FA1+→FA2=0
Запишем второй закон Ньютона в виде проекции на ось ординат:
mg=FA1+FA2
Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:
ρVg=ρ1gV1+ρ2gV2
Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:
ρV=ρ1V4+2ρ13V4
Объемы сокращаются. Остается:
ρ=ρ14+2ρ134=7ρ14=7·4004=700 (кгм3)
Ответ: 700
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
Алгоритм решения
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
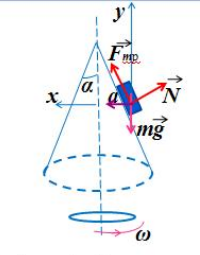
Второй закон Ньютона в векторном виде выглядит следующим образом:
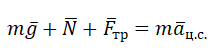
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
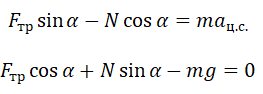
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
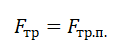
Максимальное значение силы трения равно:
![]()
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
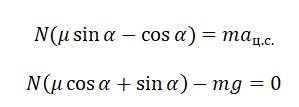
Запишем систему уравнение в следующем виде:
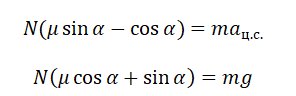
Поделим первое уравнение на второе и получим:
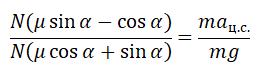
Сделаем сокращения и получим:
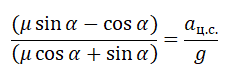
Отсюда центростремительное ускорение равно:
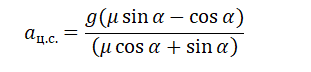
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
![]()
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
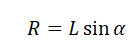
Отсюда центростремительное ускорение равно:
![]()
Выразим искомую величину L:
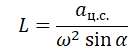
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
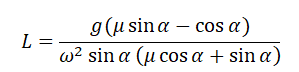
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
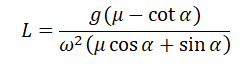
pазбирался: Алиса Никитина | обсудить разбор
👀 6.4k