Задание №17 ОГЭ по математике

площади фигур
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 3 мин.

В 17 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства. В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры. Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора? С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.

Теория к заданию №18

Приступим к разбору теории. Выпуклый четырехугольник:

выпуклый четырехугольник

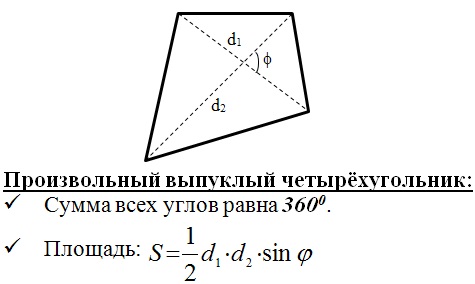
Правильный многоугольник:

  • Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
  • Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.
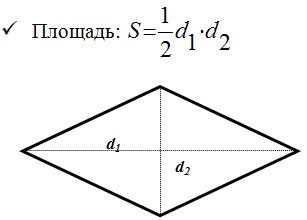
правильный многоугольник Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника: формулы многоугольников Разберем пример четырехугольника – ромб.

Параллелограмм, все стороны которого равны называется ромбом.

  • Диагональ ромба является его осью симметрии.
  • Диагонали взаимно перпендикулярны.
  • Диагонали являются биссектрисами углов.
ромб Трапеция:

Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.

трапеция
Задание 17OM21R

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула

S=a+b2..h, для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S=7+112..∙7=182..∙7=9∙7=63

Ответ: 63

pазбирался: Даниил Романович | обсудить разбор | оценить

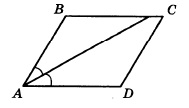
Задание OM1806o Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 41°. Ответ дайте в градусах.

Так как АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х. Поскольку АВСD параллелограмм, то ∠В+∠А=180°. Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=180°–2х. Рассмотрим ∆АВК:

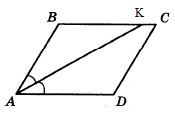
По теореме о сумме углов треугольника ∠ВАК+∠В+∠ВКА=180° По условию ∠ВКА = 41° Отсюда получаем:

х+ 180°–2х+410=180°

х–2х=1800–1800–41°

–х=–41°

х=41°

Значит, искомый (острый) ∠А=2·410=82°

Ответ: 82

pазбирался: Даниил Романович | обсудить разбор | оценить

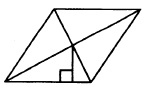
Задание OM1805o Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.

Площадь ромба будем искать по формуле:

S=ah,

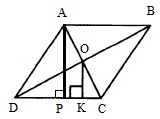
где a – сторона ромба, h– высота, опущенная на сторону а. По условию а=4. Найдем h. Для этого рассмотрим  ∆ОКС и ∆АРС: Здесь ОК || АР, причем ОК проходит через середину АС (т.к. АВСD ромб, то его диагонали в т.О делятся пополам). Значит, ОК – ср.линия ∆АРС. Поэтому АР=2ОК. Т.к. пор условию ОК=1, то АР=2·1=2. Т.о., h=АР=2. Отсюда получаем:

S=4·1=4.

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1804o Найдите площадь трапеции, изображённой на рисунке.11

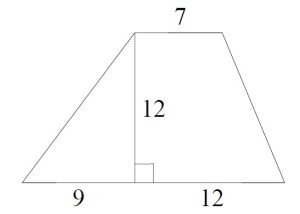
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это “полусумма оснований умноженная на высоту” Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:

  1. Верхнее основание равно 7
  2. Нижнее основание равно 9 + 12 = 21
  3. Полусумма (21 + 7) / 2 = 14
  4. Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²Ответ: 168

pазбирался: Даниил Романович | обсудить разбор | оценить

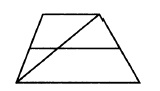
Задание OM1803o Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.решение 11 задания огэ по математике

Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:

10 / 2 = 5

11 / 2 = 5,5

Так как нас просят найти больший из отрезков, то ответ 5,5.

Ответ: 5,5

pазбирался: Даниил Романович | обсудить разбор | оценить

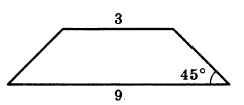
Задание OM1802o В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.решение 11 задания огэ по математике

Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:

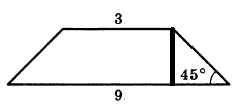
решение 11 задания огэ по математике

После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный – потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.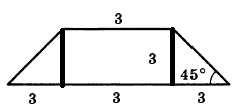решение 11 задания огэ по математике

Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.

Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:

( 9 – 3 ) / 2 = 3

А так как треугольники равнобедренные, то и высота равна 3.

Отсюда можем найти площадь:

S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18

Ответ: 18

pазбирался: Даниил Романович | обсудить разбор | оценить

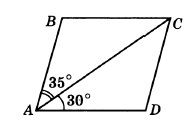
Задание OM1801o Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.решение 10 задания огэ по математике

Найдем угол BAD – это сумма углов, на которые диагональ делит этот угол, поэтому:

∠BAD = 35° + 30° = 65°

Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.

Значит:

∠ABC = ∠ADC = 180 – 65 = 115°

∠BAD = ∠BCD = 65°

Так как нас просят найти меньший угол, то это 65.

Ответ: 65

pазбирался: Даниил Романович | обсудить разбор | оценить

👀 21.9k |

9 комментариев

  5. большое спасибо до этого момента плохо разбирался а сейчас всё в порядке

  7. угол К=2* градус О+К=180* К=АВО+ВАО Треуг АВО равнобедренный, стороны радиусы, АВО=ВАО, то К=АВО+АВО=2АВО АВО=К/2=2/2=1* градус

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *