Задание №13 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 3 Среднее время выполнения: 5 мин.
В задании №13 проверяется умение решать уравнения, неравенства и их системы. Конечно, под такие слова подходит огромный спектр заданий. Уточнение, пожалуй, одно. Надо применять графическое представление решения и показа результатов этого решения. В демонстрационном варианте ОГЭ предложена система двух линейных неравенств и графические представления вариантов ответов. Полезно понимать, что главным здесь является решение конкретных неравенств и понимание геометрического смысла полученного решения.
Теория к заданию №13
Определение:
Неравенством называется выражение вида:
a < b (a ≤ b), a > b (a ≥ b)
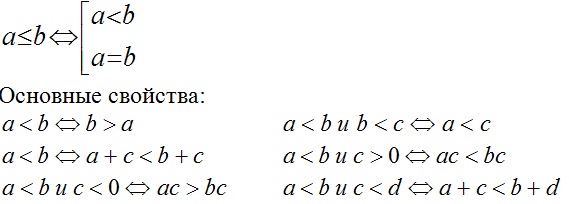
Полезным для нас окажется метод интервалов:
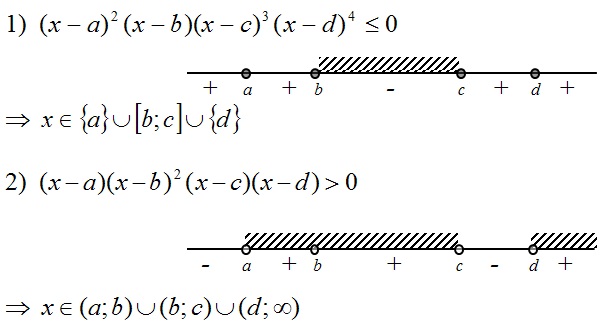
Задание 13OM21R
- [0; +∞)
- [8; +∞)
- [0; 8]
- (-∞;0]∪[8;+∞)
8х – х2≥0
Вынесем -х за скобки: -х(-8 + х) ≥0
Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – 8) ≤0
Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.
Итак, имеем нули функции 0 и 8.
Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.
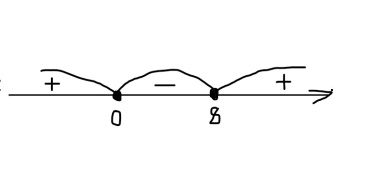
Теперь находим промежуток чисел, соответствующий неравенству х(х – 8) ≤0, т.е. промежуток отрицательных или равных нулю чисел. Это будет промежуток [0; 8]
В соответствии с его номером, это будет ответ под №3.
Ответ: 3pазбирался: Базанов Даниил | обсудить разбор
Задание OM1506o
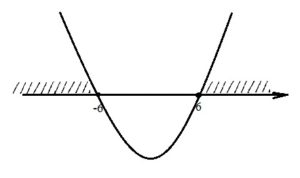
Укажите неравенство, решение которого изображено на рисунке.

Тут нужно сразу отметить два важных момента.
- Графическим решением неравенств из вариантов ответа является парабола, которая пересекает координатную ось в точках, соответствующих корням неравенств.
- Так как все неравенства, представленные в вариантах ответов, имеют нестрогий знак, то точки пересечения корней неравенства с координатной осью будут закрашенными, т.е. входящими в искомые промежутки (решения).
Анализируем неравенства.
1) х2–36≤0
х2≤36
Корни этого неравенства равны ±6. Поскольку знак неравенства «меньше», то для ответа следует взять ту часть параболы, которая располагается ниже коорд.оси. Получаем:
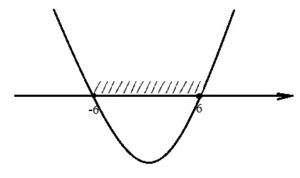
Полученный промежуток-решение не соответствует заданному в качестве ответа в условии.
2) х2+36≥0
х2≥–36
Это неравенство не имеет решений, поскольку для получения решения здесь требуется извлечь корень из отрицательные числа (из –36), а это невозможно.
3) х2–36≥0
х2≥36
Корни неравенства – ±6. Т.к. знак неравенства «больше», то для ответа следует взять ту часть параболы, которая располагается выше координатной оси. Получаем:
Здесь мы получили полное совпадение полученного решения с тем, которое представлено в условии задания.
4) х2+36≤0
х2≤–36
Тут ситуация такая же, как и во 2-м неравенства. Решений оно не имеет.
Ответ: 3pазбирался: Базанов Даниил | обсудить разбор
Задание OM1505o
Укажите решение неравенства:
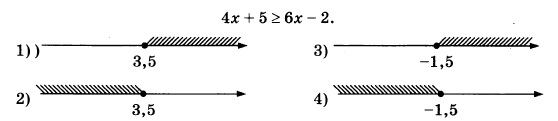
Выполняем тождественные преобразования неравенства и приводим его к простейшему виду. Для этого сначала группируем слагаемые, перенося те, что с «х», в левую сторону, а свободные члены в правую:
4х–6х≥–2–5
Приводим подобные:
–2х≥–7
Находим х. Знак неравенства при этом поменяется на противоположный, поскольку делить будем на –2, т.е. на отрицательное число:
х≤3,5
Далее на коорд.прямой теперь нужно отложить точку со значением 3,5, причем точка будет закрашенная, т.к. знак неравенства нестрогий:
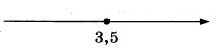
Т.к. знак полученного неравенства «≤», то выделить следует часть прямой слева от точки 3,5:
![]()
Это графическое решение соответствует ответу под №2.
Ответ: 2pазбирался: Базанов Даниил | обсудить разбор
Задание OM1504o
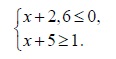 На каком рисунке изображено множество её решений?
На каком рисунке изображено множество её решений?
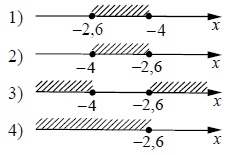
Итак, решим систему неравенств — оставим х в левой части, а остальное перенесём в правую, получим:
х ≤ 0 -2,6
х ≥ 1 — 5
Вычислив, получаем ответ:
х ≤ -2,6
х ≥ -4
Найдем его на координатной прямой — это №2.
Ответ: 2pазбирался: Базанов Даниил | обсудить разбор
Задание OM1503o
Укажите множество системы неравенств:
⌈ x - 4 ≥ 0
⌊ x - 0,3 ≥ 1
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:
⌈ x ≥ 4
⌊ x ≥ 1,3
В отличие от первого примера, решение более простое, но в данном случае нужно сравнить промежутки и выбрать общий. Первое неравенство требует, чтобы x был больше 4, а второе — более 1,3, на координатной прямой это будет выглядеть следующим образом:
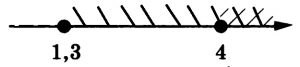
Промежутки перекрывают друг друга начина с 4, значит ответ выглядит следующим образом (не забываем, что неравенство нестрогое):
[ 4 ; + ∞ ) или
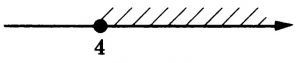
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1502o
Укажите множество решений неравенства: 7 x - x2 < 0
Существуют несколько способов решения квадратных неравенств, но я приведу самый простой и надежный. В начале выносим x за скобку, так как это неполное квадратное неравенство:
x ( 7 — x ) < 0
Затем находим ноли функции x ( 7 — x ) = 0, приравнивая каждый множитель к нолю:
x = 0
7 — x = 0
Получаем:
x = 0
x = 7
Таким образом, мы получили три интервала:
( -∞ ; 0 )
( 0 ; 7 )
( 7 ; +∞)
Подставим любое значение x из первого интервала и посмотрим на получившийся ответ.
Подставим -1:
x ( 7 — x ) = — 1 ( 7 — (-1) ) = -8
Значение отрицательно, значит в интервале ( -∞ ; 0 ) функция отрицательна, что нам и подходит для ответа, так как в условии:
x ( 7 — x ) < 0
Подставим 1:
x ( 7 — x ) = 1 ( 7 — 1 ) = 6
Значение положительно, и промежуток ( 0 ; 7 ) нам не подходит.
Подставим 8:
x ( 7 — x ) = 8 ( 7 — 8 ) = — 8
Значение отрицательно, и это подходит под условия, следовательно ответ:
( -∞ ; 0 ) и ( 7 ; +∞)
или графически:
![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM1501o
Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений. Однако, в отличие от линейных уравнений следует проявлять внимательность при выполнении операций деления или умножения на отрицательное число — в этих случаях знак неравенства будет меняться на противоположный!
Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает + 21:
2 x — 3 x + 21 ≤ 3
Затем приводим подобные, перенося числа в правую сторону:
2 x — 3 x ≤ 3 — 21
— x ≤ -18
Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:
x ≥ 18
Таким образом, мы получаем, что x должен быть больше либо равен 18.
Ответ: [18;+∞)pазбирался: Базанов Даниил | обсудить разбор
👀 40.3k
Прекрасный разбор задания