Задание №25 ОГЭ по математике
Первичный бал: 1 Сложность (от 1 до 3): 3 Среднее время выполнения: 15 мин.
Решаем сложную геометрическую задачу.
Задание 25OM21R
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
AEAB=ABAF откуда по свойству пропорции АВ2=АЕ∙АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
AEAD=ACAF ; откуда выразим AD=AE∙AFАC=AE∙AFAC
Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC
Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD=AE∙AFAC=36254=24
Теперь найдем CD=AC-AD=54-24=30
Ответ: 30pазбирался: Базанов Даниил | обсудить разбор
Задание OM2604o
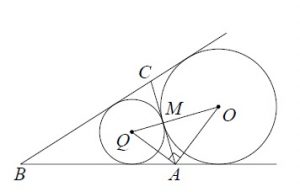
Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .
Точка касания M окружностей делит AC пополам по условию.
Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:
180°/2 = 90°.
Далее рассмотрим прямоугольный треугольник OAQ. По свойству высоты в прямоугольном треугольнике, получаем:
AM² = MQ•MO
Отсюда:
QM = AM² / MO
QM = 6² / 8 = 4,5
Ответ: 4,5pазбирался: Базанов Даниил | обсудить разбор
Задание OM2603o
Алгоритм решения:
- Сделаем чертеж.
- Установим подобие треугольников AFM и ANF.
- Определим сторону FM.
- Определим ∠FNA.
- Найдем .
- Составим теорему синусов и найдем радиус окружности.
- Запишем ответ.
Решение:
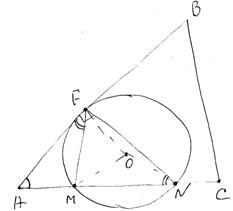
1. Рассмотрим треугольники AFM и ANF. У них:
Угол A является общим, а
![]() по доказанному выше.
по доказанному выше.
Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:
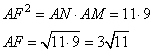
3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:
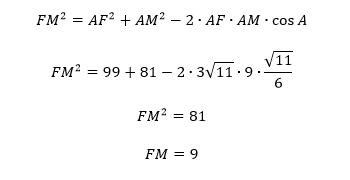
Полученное значение означает, что AFM является равнобедренным. У него основание AF.
4. По свойству равнобедренного треугольника ∠FAM=∠AFM. Отсюда
![]()
5. Найдем
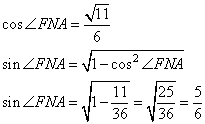
Значит,
![]()
6. Из FMN по теореме синусов:
![]()
где R – радиус описанной окружности.
Отсюда получим значение радиуса окружности:
![]()
pазбирался: Базанов Даниил | обсудить разбор
Задание OM2602o
Алгоритм решения:
- Сделаем чертеж.
- Определим равенство углов CDB и АВС.
- Определим соотношение отрезков, воспользовавшись свойством биссектрисы угла треугольника, и определим длину АВ.
- Покажем, что треугольники DAC и DCB подобны.
- Составим соотношения сторон подобных треугольников.
- Составим систему равенств.
- Решим систему.
- Запишем ответ.
Решение:
1. Делаем чертеж.
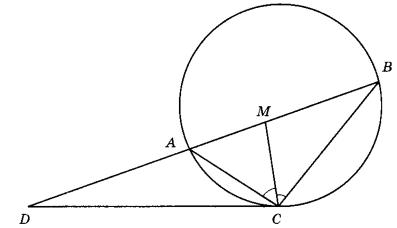
2. Рассмотрим АСD. В нем, согласно свойству углов окружности, касательной и секущей,
угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла.
⇒∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, согласно которому она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,
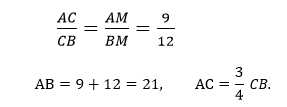
4. Рассмотрим DAC и DCB. У них:
∠ DCA = ∠ DBC по доказанному выше,
∠ D – общий.
Значит, DAC DCB по двум углам.
5. Из определения и свойств подобных треугольников имеем:
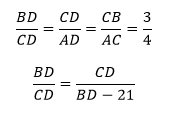
6. Составим систему равенств:
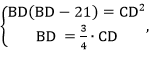
7. Решим систему:
![]()
Отсюда
![]()
![]()
Так как AD = DB-21, имеем:

Таким образом, искомая длина CD=36.
Ответ: 36pазбирался: Базанов Даниил | обсудить разбор
Задание OM2601o
Алгоритм решения:
- Делаем чертеж.
- Определяем равенство угла между касательной и хордой и угла АВС.
- Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
- Показываем, что треугольники DAC и DCB подобны.
- Составляем соотношения сторон подобных треугольников.
- Составляем систему равенств.
- Решаем систему.
- Записываем ответ.
Решение:
1. Выполняем чертеж данной задачи:
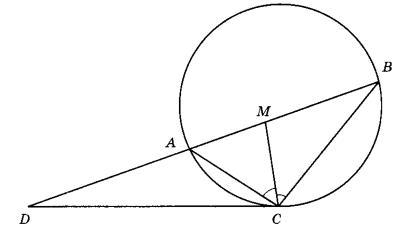
2. Рассматриваем АСD. В нем:
Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,
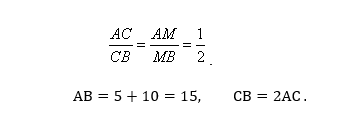
4. Рассмотрим DAC и DCB. У них:
∠ DCA = ∠ DBC по доказанному выше,
∠ D – общий.
Следовательно, DAC DCB по двум углам.
5. Из определения и свойств подобных треугольников имеем:
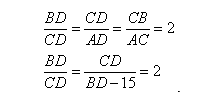
6. Составим систему равенств:
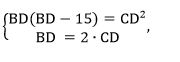
7. Решим систему:

pазбирался: Базанов Даниил | обсудить разбор
👀 15.4k
почему только 1 вариант?
Скоро добавим, не переживайте, нам нужно время, чтобы наполнять все разделы равномерно!
Благодарю Вас!
Прекрасная работа. Спасибо. Побольше бы такой информации.