Задание №21 ОГЭ по математике
Первичный бал: 2 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
В двадцать втором задании необходимо решить задачу, составив уравнение с неизвестными. Ниже мы приводим алгоритмы решения типовых вариантов.
Задание 21OM21R
Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:
| Скорость | Время | Расстояние | |
| 1 автомобиль | х | 800х | 800 |
| 2 автомобиль | х — 36 | 800х−36 | 800 |
Пояснения к заполнению таблицы:
Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.
Расстояние у каждого авто будет 800 км.
Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.
Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:
800х−36− 800х=5
Приведем к общему знаменателю х(х-36) наше уравнение и решим его:
800х – 800(х-36)=5х(х-36)
800х – 800х+28800=5х2 – 180
28800=5х2 – 180
5х2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:
х2 – 36 – 5760=0
Решим полученное квадратное уравнение
D=b2 – 4ac=362 — 4∙(−5760)=24336
х1,2=−b±√D2a=36±1562
Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.
Значит, скорость первого автомобиля 36 км/ч
Ответ: 36pазбирался: Базанов Даниил | обсудить разбор
Задание OM2206o
Алгоритм решения:
- Вводим переменные-обозначения для скорости наполнения резервуара (л/мин) и для времени наполнения (мин). Выражаем через соответствующие переменные параметры наполнения для 1-й и 2-й труб.
- Составляем систему уравнений (1-е уравнение для первой трубы, 2-е – для второй).
- Решаем систему.
Решение:
Обозначим через х скорость наполнения 1-й трубы (это наша искомая величина). Тогда скорость наполнения 2-й трубы равна (х+5).Обозначим через t время наполнения 2-й трубы. Тогда время наполнения 1-й трубы составит (t+2).
Через каждую из труб должно пройти 200 л воды.
Для 1-й трубы получим:
x(t+2)=200
Аналогично для 2-й трубы:
(x+5)t=200
Из уравнения для 2-й трубы выразим t через х:
t=200/(x+5)
Подставим полученное для t выражение в уравнение для 1-й трубы:
![]()
Решим это уравнение и найдем искомую величину:
![]()
x(210+2x)=200(x+5)
210х+2х2=200х+1000
2х2+210х–200х–1000=0
2х2+10х–1000=0
х2+5х–500=0
По теореме Виета х1=20, х2=–25
Корень х2 не может быть принят в качестве ответа, поскольку он не удовлетворяет условию (скорость наполнения резервуара не может быть отрицательной величиной).
Значит, искомая скорость наполнения равна 20 л/мин.
Ответ: 20pазбирался: Базанов Даниил | обсудить разбор
Задание OM2205o
Алгоритм решения:
- Находим число процентов (или долю) твердого вещества в свежих фруктах. Находим эту величину в кг.
- Вычисляем кол-во процентов твердого вещества в сушеных фруктах.
- Составляем пропорцию и определяем общую массу сушеных фруктов.
Решение:
Если воды в свежих фруктах 88%, то твердого вещества (мякоти) в них 100%–88%=12%=0,12.
В кг эта масса равна 35·0,12=4,2 (кг).
В сушеных фруктах масса твердого вещества, по сравнению со свежими, не меняется (а только снижается объем воды). Поэтому в искомой массе сухих фруктов мякоти тоже будет 4,2 кг. Но в процентном соотношении эта масса составит 100%–30%=70% (30% по условию приходится на воду). Искомая же (общая) масса сухих фруктов в данном случае – это 100%.
Тогда обозначим искомую массу через Х и составим пропорцию:
4,2 кг – 70%
Х – 100%
Решим эту пропорцию:
Х=4,2·100%/70%=6 (кг)
Ответ: 6pазбирался: Базанов Даниил | обсудить разбор
Задание OM2204o
Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно
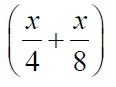 часа.
часа.
Из условия задачи следует, что это время равно 3 часам. Составим уравнение:
![]()
Решая уравнение, получаем x = 8.
Ответ: 8pазбирался: Базанов Даниил | обсудить разбор
Задание OM2203o
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км | |
| 1 велосипедист | 24 | t +9 | |
| 2 велосипедист | 21 | t +1 | |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Второй велосипедист до момента, когда его догонит третий велосипедист, двигался t + 1 часов . Он проехал до места встречи 21·(t + 1) км.
Расстояния, пройденные велосипедистами, одинаковы. Получим первое равенство x·t = 21·(t + 1).
Третий велосипедист до момента встречи с первым велосипедистом после встречи о вторым, ехал t + 9 ч тогда до места встречи с первым велосипедистом он проехал расстояние x·(t + 9) км.
Первый велосипедист до встречи с третьим ехал t + 11 часов, поскольку до момента выезда третьего, уже проехал 2 часа. До места встречи он проехал 24·(t + 11) км.
Расстояния одинаковы. Тогда получим еще одно равенство: x·(t + 9) = 24·(t + 11)
Составим систему уравнений для решения задачи:
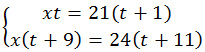
Решим ее, раскрыв скобки и преобразовав каждое уравнение:
![]()
Далее используем метод вычитания, откуда получим:
9x = 3t + 243
3x = t + 81
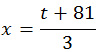
Подставив выражение для x в первое уравнение:
![]()
Получили квадратное уравнение.
t2 + 81t = 63t + 63
Решим его:
t2 + 18t – 63 = 0
D = b2 – 4ac
D = 182 — 4·1·(-63) = 324 + 252 = 576
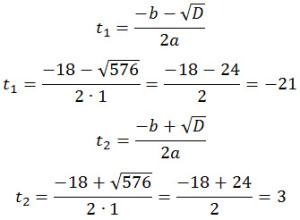
Первое значение не подходит, поскольку время по условию не может иметь отрицательные значения. Значит,
![]()
Таким образом, скорость третьего велосипедиста 28 км/ч.
Ответ: 28pазбирался: Базанов Даниил | обсудить разбор
Задание OM2202o
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км | |
| 1 велосипедист | 15 | t +7 | |
| 2 велосипедист | 10 | t +1 | |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).
Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.
Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.
Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)
4. Составляем систему уравнений:
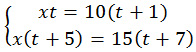
5. Решаем полученную систему, преобразовав каждое из уравнений:
![]()
Вычитаем из второго уравнение первое, получаем
5x = 5t + 95
x = t + 19
Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.
(t + 19)·t = 10t + 10
t2 + 19t = 10t + 10
t2 + 9t – 10 = 0
По формуле дискриминанта и корней:
D = b2 – 4ac
D = 92 — 4·1·(-10) = 81 + 40 = 121
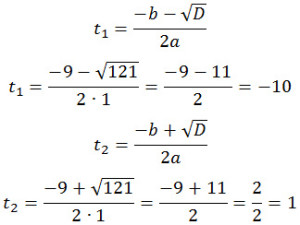
Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,
x = t + 19 = 1 + 19 = 20
Скорость третьего велосипедиста 20 км/ч.
Ответ: 20pазбирался: Базанов Даниил | обсудить разбор
Задание OM2201o
Алгоритм решения:
- Введем неизвестную величину: скорость третьего.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Выясняем, на какой вид движения эта задача.
- Используя условие, формулы времени или скорости, выражаем через неизвестную величину все остальные.
- Исходя из условия, составляем равенство и преобразуем его.
- Решаем уравнение.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Обозначим через x км/ч скорость третьего велосипедиста.
2. Составим таблицу их краткого условия:
| v, км/ч | t, ч | S, км | |
| 1 велосипедист | 21 | На 2 ч раньше всех | |
| 2 велосипедист | 15 | На 1 ч раньше третьего | |
| 3 велосипедист | х |
3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.
4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя ![]() ч после своего выезда.
ч после своего выезда.
Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через ![]() ч после своего выезда из поселка.
ч после своего выезда из поселка.
По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.
5. Исходя из этого, составим равенство:
![]() ,
,
Преобразуем полученное уравнение:

6. Получили квадратное уравнение. Решим его:
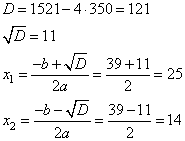
По условию скорость третьего велосипедиста была наибольшей, значит, второй корень не удовлетворяет условию. Получаем. Что решением будет x = 25 км/ч.
Ответ: 25pазбирался: Базанов Даниил | обсудить разбор
👀 38.9k
очень удобно!
Спасибо-о-о!!!! Оказалось задание очень простое)
2 вариант (х* это х в квадрате, в степени 2) …=х*(х+4)-9(х+4)=(х*-9)(х+4)=0 х*-9=0 х*=9 х=3;—3 х+4=0 х=—4
3 вариант …=х*(х+2)-1(х+2)=(х*-1)(х+2)=0 х*-1=0 х*=1 х=1;—1 х+2=0 х=—2
А можно пожалуйста разбор на задачу номер 21 где идёт пешеход едет поезд и нужно найти длину поезда
Узнал про схему Горнера,Спасибо большое
Уравнения третьей степени лучшерешть способом группировки. Быстрее. короче.
В последней задаче при решении вероятно допущена описка при решение целого уравнения — 180, (180 х) и далее , а также в ответе: 36 (96). Спасибо за вашу работу!
Спасибо, но где задачи на производительность? Очень удобно, только еще задачи на производительность добавьте пожалуйста, тогда будет все вообще идеально))))))
К последнему заданию. Как извлечь корень из 24336? На Оге нет таблицы квадратов больше 100.
подбирать придется