Задание №24 ОГЭ по математике

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

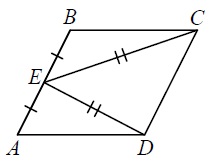
Рассмотрим треугольники BEC и AED. BE = EA, так как E — середина стороны AB по условию. EC= ED по условию, а BC = AD по свойству параллелограмма (противолежащие стороны равны). Таким образом, BE = EA, EC= ED, BC = AD. Следовательно, треугольники BEC и AED равны по трём сторонам.

В равных треугольниках — равные элементы. Значит, углы CBE и DAE равны. Так как их сумма равна 180° по свойству параллелограмма , то углы равны 90° (180 / 2 = 90 ) .

Следовательно, данный параллелограмм — прямоугольник.

Алгоритм решения:

1. Выполняем рисунок по условию задачи.
2. Устанавливаем подобие треугольников BOC и AOD.
3. Записываем соотношение для сторон.
4. Устанавливаем подобие треугольников AOB и DOC.
5. Делаем вывод.

Решение:

1. Выполняем чертеж по условию задачи:

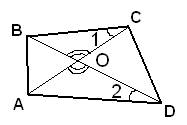
2. Рассматриваем треугольники BOC и AOD.У них:

углы ВСА и BDA равны по условию задачи,

углы BOC и AOD равны как вертикальные.

Значит, треугольники BOC и AOD подобны по двум углам.

3. Для подобных треугольников BOC и AOD записываем соотношение соответствующих сторон:

4. Рассматриваем треугольники AOB и DOC. У них:

углы AOB и DOC равны как вертикальные.

Следовательно, данные треугольники подобны.

По свойству подобных фигур соответствующие углы в треугольниках равны. Значит, , а поскольку эти углы совпадают с углами ABD и ACD , то .

Алгоритм решения:

1. Делаем чертеж по условию задачи.
2. Рассмотрим треугольники SMN и TMN и установим их равенство.
3. Воспользуемся свойством равных фигур для определения вида треугольника SMT.
4. Используем свойство равнобедренного треугольника и делаем вывод.

Решение:

1. Делаем чертеж согласно условия задачи.

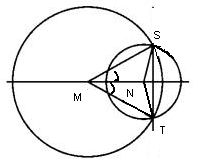
2. Рассмотрим треугольники SMN и TMN. Они равны по трем сторонам:

SM=TM как радиусы окружности с центром в точке М,

SN=TN как радиусы окружности с центром в точке N,

а MN – общая сторона (см. рисунок выше).

3. По свойству равных фигур,  , как соответствующие углы в равных треугольниках.

4. Рассмотрим треугольник SMT.

В нем по доказанному выше , а значит MN – биссектриса угла M. Данный треугольник равнобедренный с равными сторонами SM и TM.

Следовательно, MN – высота по свойству биссектрисы равнобедренного треугольника. Следовательно, .

Алгоритм решения:

1. Делаем чертеж по условию задачи.
2. Рассмотрим треугольники CEF и DEF и установим их равенство.
3. Воспользуемся свойством равных фигур для определения вида треугольника CED.
4. Используем свойство равнобедренного треугольника и делаем вывод.

Решение:

1. Делаем чертеж по условию задачи:

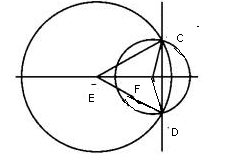
2. Рассмотрим треугольники CEF и DEF и установим их равенство:

У них CE=DE, как радиусы окружности с центром в точке Е,

Аналогично, CF = DF, как радиусы окружности с центром в точке F.

EF – общая сторона.

Значит, данные треугольники равны.

Тогда по свойству равных фигур .

Рассмотрим треугольник CED. У него CE=DE, поскольку это соответствующие стороны равных фигур. Значит, треугольник равнобедренный.

EF – биссектриса угла E. следовательно, EF – высота по свойству равнобедренного треугольника. Отсюда следует, что .

Алгоритм решения:

1. Делаем чертеж.
2. Определяем место расположения точек I и J.
3. Используем свойство серединного перпендикуляра.
4. Делаем вывод.

Решение:

1. Делаем чертеж, согласно условия:

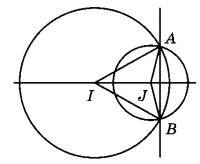
2. Определяем место расположения точек I и J:

Точка I равноудалена от точек A и B. Аналогично, точка J равноудалена от концов отрезка AB.

3. По свойству геометрического места точек, равноудаленных от концов отрезка, эти точки расположены на серединном перпендикуляре к отрезку AB.

А если две точки I и J лежат на серединном перпендикуляре, прямая IJ совпадает с ним. Следовательно, прямые IJ и АВ перпендикулярны.