Задание №30 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Для решения задания № 30 требуется знание как основ МКТ, так и базовых понятий термодинамики. Кроме этого, вероятно применение при этом величин (законов и т.д.) из гидроаэродинамики. Распространенным при решении заданий такого плана является использование тех или иных табличных данных.
Задание ЕГЭ-Ф-ДВ2023-30(1)
Алгоритм решения:
Решение:
Запишем исходные данные:
Переводим единицы измерения величин в СИ:
M = 230 г = 0,23 кг
l = 50 см = 0,5 м
Систему отсчёта, связанную с Землёй, будем считать инерциальной. Тела считаем материальными точками.
Для описания взаимодействия пули и шара используем закон сохранения импульса системы тел. Он выполняется в инерциальной системе отсчёта, если сумма внешних сил, приложенных к телам системы, равна нулю. В данном случае проекции внешних сил (силы тяжести и силы натяжения нити) на горизонтальную ось в момент взаимодействия равны нулю. Следовательно, можно использовать закон сохранения импульса в проекциях на эту ось.
Для дальнейшего движения шара с застрявшей в нём пулей будет справедлив закон сохранения механической энергии, поскольку сопротивлением воздуха по условию задачи можно пренебречь, а единственная неконсервативная сила, действующая на шар, – сила натяжения нити – не совершает работы при движении шара по окружности, поскольку она всюду перпендикулярна скорости движения шара.
Условие минимальности v0 означает, что шар совершает полный оборот в вертикальной плоскости, но при этом натяжение нити в верхней точке (и только в ней) равен 0.
Применим закон сохранения импульса, согласно которому сумма импульсов всех сил в системе не меняется до и после их взаимодействия. Следовательно:
![]()
Так как начальная скорость V шара равна нулю:
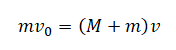
Скорость v — скорость движения шара и пули, которые после столкновения движутся как единое тело с массой M + m.
Теперь применим закон сохранения энергии. Учитываем, что в момент столкновения система тел имела максимальную скорость, а соответственно — максимальную кинетическую энергию. Также учитываем, что в верхней точке движения кинетическая энергия системы тел была меньше за счет уменьшения скорости, но не была нулевой. Также в верхней точке траектории система тел обладала максимальной потенциальной энергией. Запишем это так:
![]()
Максимальная кинетическая энергия системы тел будет равна:
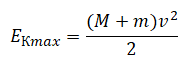
Кинетическая энергия в верхней точке:
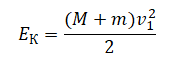
v1 — скорость системы тел в верхней точке.
Потенциальная энергия равна произведению массы системы тел на ускорение свободного падения и на высоту, на которой находится система в верхней точке — h. Эта высота равна удвоенной длине нити:
![]()
Тогда закон сохранения энергии принимает вид:
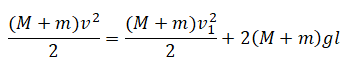
Также применим законы Ньютона к системе тел в верхней точке траектории. С одной стороны, на нее действует сила тяжести Fтяж=(M+m)g. С другой — центробежная сила — FЦ=(M+m)v21l... В знаменателе используем длину нити, так как она в данном случае равна радиусу окружности, по которой происходит движение системы тел.
Модули этих сил равны. Следовательно:
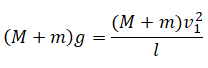
Или:
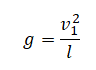
Отсюда выразим квадрат скорости в верхней точке:
![]()
Подставляем это выражение в закон сохранения энергии:
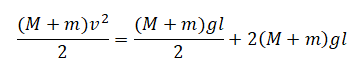
Или:
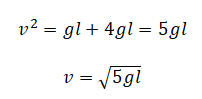
Подставляем эту скорость в закон сохранения импульса и выразим из него массу пули:
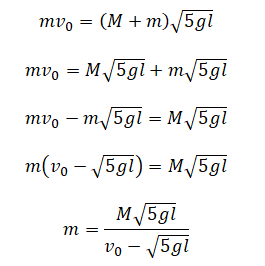
Подставляем известные значения и находим массу пули:
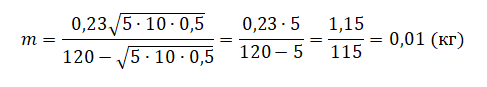
pазбирался: Алиса Никитина | обсудить разбор
Задание ЕГЭ-Ф-ДВ2023-30(2)
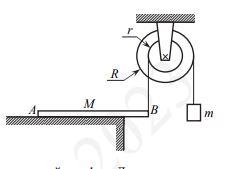 Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем
из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая
нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое. R = 10 см, r = 5 см. Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.
Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем
из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая
нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое. R = 10 см, r = 5 см. Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.Алгоритм решения:
Решение:
Запишем исходные данные:
Переведем единицы измерения в СИ:
R = 10 см = 0,1 м
r = 5 см = 0,05 м
Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО).
Брусок перед отрывом его правого края от поверхности стола будем считать твёрдым телом с осью вращения, проходящей перпендикулярно плоскости рисунка через точку A. Условие равновесия относительно вращения твёрдого тела на оси — равенство нулю суммы моментов сил, приложенных к телу, относительно этой оси.
Нити нерастяжимы, поэтому, если покоится брусок, то покоятся и все остальные тела системы.
Нити лёгкие, поэтому величина силы натяжения каждой нити в любой её точке одна и та же. В том числе: T1 = T3,T2 = T4 (см. рисунок в решении).
Блок идеальный (трения в осях нет, масса блока пренебрежимо мала). Поэтому условие равновесия блока – равенство нулю суммы моментов сил натяжения нитей относительно оси блока.
Груз может двигаться только поступательно вдоль вертикальной оси Oy, лежащей в плоскости рисунка. Поэтому для груза используем модель материальной точки и применим второй закон Ньютона. Вследствие этого условие равновесия — сумма приложенных к грузу сил равна нулю.
Сделаем поясняющий рисунок:
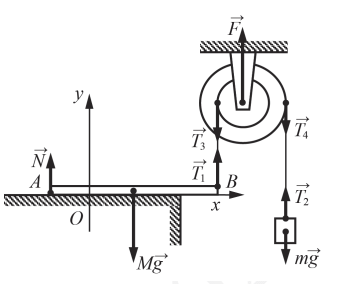
На рисунке представлен случай, когда масса бруска минимальна. Поэтому он еще покоится на столе, но касается стола только в точке А. Силы, действующие на брусок:
Силы, действующие на блок:
Силы, действующие на груз:
Запишем уравнение моментов сил для бруска в момент, когда он покоится, касаясь стола только в точке A:
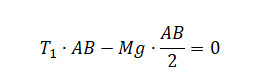
Или:
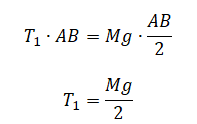
Запишем второй закон Ньютона для покоящегося груза в проекциях на ось Oy введённой ИСО:
![]()
Или:
![]()
Запишем условие равновесия блока на его оси. Блок будет находится в равновесии тогда, когда будут равны моменты сил:
![]()
Учитываем, что сила натяжения нити 1 равно силе натяжения нити 3, а 2 — 4. Тогда это выражение принимает вид:
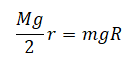
Или:
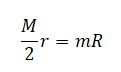
Отсюда масса бруска равна:
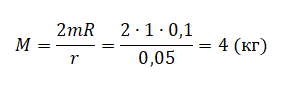
pазбирался: Алиса Никитина | обсудить разбор
Задание Статика 1
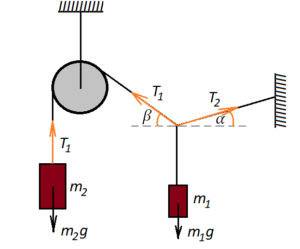 Грузы
Грузы Алгоритм решения:
Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО).
Нити лёгкие, поэтому величина силы натяжения каждой нити в любой её точке одна и та же.
Блок идеальный (трения в осях нет, масса блока пренебрежимо мала). Поэтому условие равновесия блока – равенство нулю суммы моментов сил натяжения нитей относительно оси блока.
Система находится в равновесии, потому можем применять 2 закон Ньютона следующим образом. Поскольку груз m2 покоится, условием его равновесия будет:
![]()
Поскольку груз m1 покоится, условием его равновесия будет:
![]()
В точке, к которой приложены силы натяжения нити 1 и 2, условие равновесия следующие (относительно оси Ох):
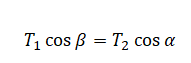
Применив закон Ньютона, остается только сделать преобразования формул. Так, масса груза 1 будет равна:
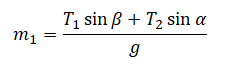
Выше уже выяснили, что сила натяжения нити 1 равна силе тяжести груза 2, масса которого известна. Следовательно, неизвестна лишь сила натяжения нити 2, которую можем выразить через силу натяжения 1 и косинусы углов:

Следовательно:
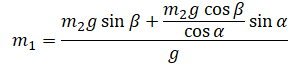
Упростим выражение:
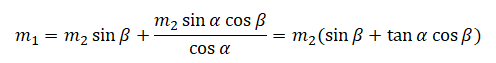
pазбирался: Алиса Никитина | обсудить разбор
Задание Статика 2
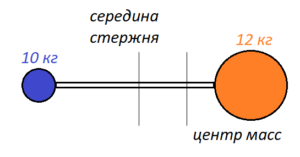 Два однородных шара массами 10 и 12 кг с радиусами 4 и 6 см соединены посредством однородного стержня массой 2 кг и длиной 10 см. Центры шаров лежат на продолжении оси стержня. Найти расстояние в см от центра тяжести этой системы до оси, проходящей через середину стержня.
Два однородных шара массами 10 и 12 кг с радиусами 4 и 6 см соединены посредством однородного стержня массой 2 кг и длиной 10 см. Центры шаров лежат на продолжении оси стержня. Найти расстояние в см от центра тяжести этой системы до оси, проходящей через середину стержня.Алгоритм решения:
Решение:
Запишем исходные данные:
СИ не соответствует только мера длины. Но так как все длины приведены в сантиметрах, мы можем условиться использовать их. Но тогда все полученные результаты в вычислениях длин будут представлены в сантиметрах — именно в них по условию задачи нужно определить расстояние от центра тяжести этой системы до оси, проходящей через середину стержня.
Так как шары однородные, можем считать, что центры их масс находятся в центре шаров. По этой же причине все центры масс лежат на одной прямой. Всю систему тел можем считать твердым телом с осью вращения в точке, которая лежит на расстоянии x от оси, проходящей через середину стержня.
Чтобы найти искомую величину, вспомним, что система будет находиться в равновесии, если ось вращения будет проходить через ее центр масс. А условие равновесия относительно вращения твёрдого тела на оси — равенство нулю суммы моментов сил, приложенных к телу, относительно этой оси. Сделаем рисунок и запишем это условие равновесия, учитывая следующее:
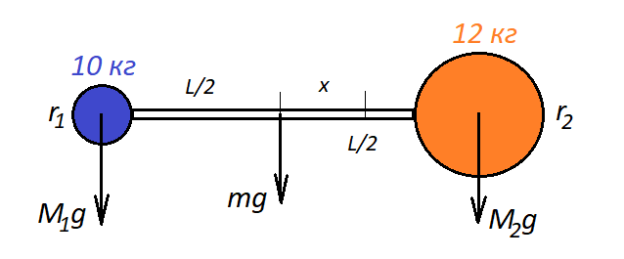
Учитывая сказанное выше, условие равновесия системы принимает вид:
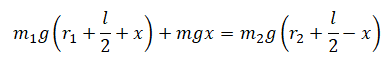
Или:
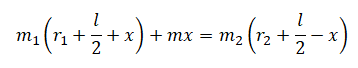
Все величины, кроме искомой, являются известными. Можно было бы упросить выражение, но в условиях данной задачи будет проще сразу подставить известные величины, а затем произвести необходимые вычисления:
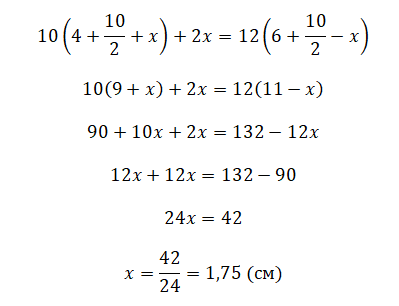
.
.
.
.
Ответ: 1,75pазбирался: Алиса Никитина | обсудить разбор
Задание Статика 3
Алгоритм решения:
Решение:
Запишем исходные данные:
Чтобы все единицы были соразмерны, переведем их в СИ:
L = 25 см = 0,25 м
l = 10 см = 0,1 м
S = 0,1 см2 = 10–5 м2
ρал = 2,7 г/см3 =2700 кг/м3.
ρв = = 1 г/см3 =1000 кг/м3
Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО). По условию задачи спица однородная. Нить будем считать невесомой. Система тел находится в состоянии равновесия. Поэтому будем применять правило моментов сил.
Сделаем поясняющий рисунок, учитывая следующее:
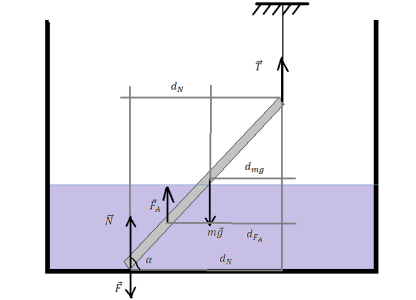
Так как сила трения отсутствует, можем модуль искомой силы F принять за модуль силы нормальной реакции опоры. Следовательно, вся задача сводится к вычислению N.
Будем рассматривать равновесие системы относительно верхнего конца спицы. К этой точке приложена сила натяжения нити. Поэтому ее плечо равно 0. Следовательно, момент силы натяжения нити равен 0.
Плечо силы нормальной реакции опоры будет равно произведению длины спицы на косинус угла α:
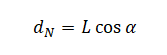
Плечо силы Архимеда будет равно произведению косинуса угла α на разность длины спицы и половины длины погруженной части спицы:
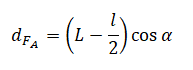
Плечо силы тяжести будет равно половине длины спицы на косинус угла α:
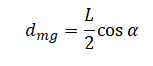
Учитывая направление сил относительно вертикали, составляем условие равновесия:
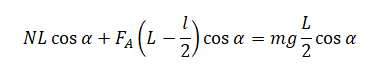
Поделим на косинус и получим:

Сила Архимеда равна произведению плотности жидкости на ускорение свободного падения и объем погруженной части тела. Этот объем равен произведения площади поперечного сечения спицы на длину погруженной части:
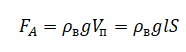
Сила тяжести равна произведения массы на ускорение свободного падения. А массу можем найти как произведение плотности алюминия, из которого сделана спица, на объем спицы. А объем равен произведению длины на площадь поперечного сечения:
![]()
Следовательно, условие равновесия принимает вид:
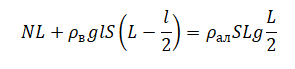
Выразим искомую величину:
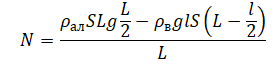
Считаем:
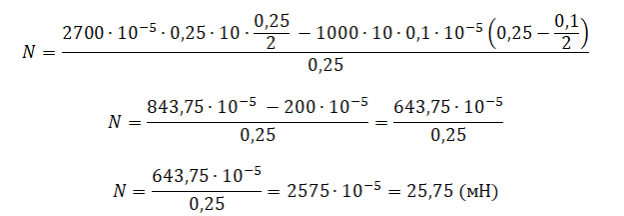
Следовательно, спица давит на дно с силой 25,75 мН.
.
.
.
.
Ответ: 25,75pазбирался: Алиса Никитина | обсудить разбор
Задание Статика 4
 Два небольших шара массами m1 = 0,2 кг и m2 = 0,3 кг закреплены на концах невесомого стержня AB, расположенного горизонтально на опорах C и D (см. рис.). Расстояние между опорами l = 0,6 м, а расстояние AC равно 0,2 м. Чему равна длина стержня L, если сила давления стержня на опору D в 2 раза больше, чем на опору C? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень — шары».
Два небольших шара массами m1 = 0,2 кг и m2 = 0,3 кг закреплены на концах невесомого стержня AB, расположенного горизонтально на опорах C и D (см. рис.). Расстояние между опорами l = 0,6 м, а расстояние AC равно 0,2 м. Чему равна длина стержня L, если сила давления стержня на опору D в 2 раза больше, чем на опору C? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень — шары».Алгоритм решения:
Решение:
Запишем исходные данные:
Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО). Стержень невесомый, сила трения отсутствует. Потому можем сделать рисунок и указать на нем силы следующим образом:
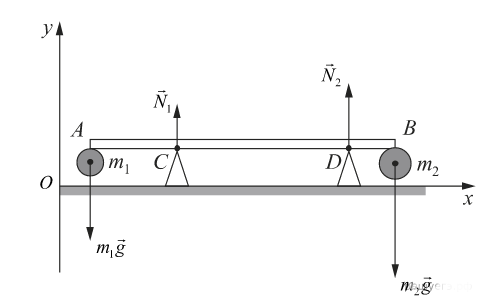
К опорам C и D приложены только силы нормальной реакции опоры 1 и 2. Следовательно, модули сил давления будут соответственно равны силам нормальной реакции опоры 1 и 2:

Отсюда отношение второй силы нормальной реакции опоры ко второй равно:
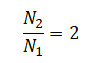
Или:
![]()
Так как центр масс не движется вдоль оси Оу, можем записать следующее условие равновесия системы тел:
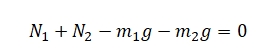
Так как нет вращения вокруг оси, которая проходит через точку А перпендикулярно рисунку:
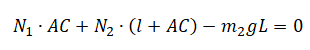
Подставим силу реакции 2, выраженную через силу реакции 1:
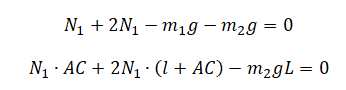
Преобразуем уравнения:
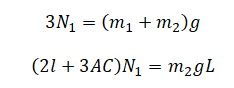
Из верхнего уравнения выразим силу реакции 1 и подставим выражение в нижнее уравнение:

Выразим длину стержня и сделаем необходимые преобразования:
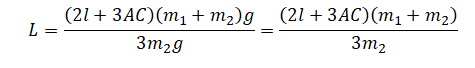
Вычислим:
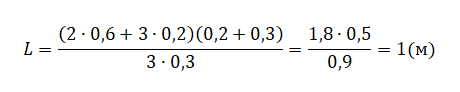
pазбирался: Алиса Никитина | обсудить разбор
Задание Статика 5
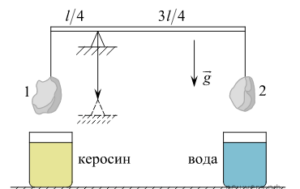 К концам лёгкого стержня длиной l, лежащего на клиновидной опоре, установленной на расстоянии
К концам лёгкого стержня длиной l, лежащего на клиновидной опоре, установленной на расстоянии Алгоритм решения:
Решение:
Запишем исходные данные:
Нет необходимости переводить единицы измерения в СИ.
Будем считать, что система тел находится в инерциальной системе отсчета. Условимся, что все тела в ней неподвижные, а стержень жесткий, тела при погружении в жидкости не касаются дна и стенок сосудов. Поэтому можем использовать законы статики и гидростатики — условия равновесия твердого тела в инерциальной системе отсчета и закон Архимеда. Так как нити по условию невесомые, будем считать, что сила натяжения в каждой точке одинакова.
Введём инерциальную систему отсчёта — далее в ней будем рассматривать проекции всех сил на вертикальную ось, так как сил, направленных по горизонтали, не наблюдается.
Стержень в обоих случаях является неподвижным, поэтому моменты сил натяжения нитей слева и справа от точки опоры направлены противоположно и одинаковы:
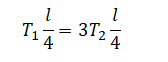
Отсюда следует:
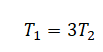
На каждый из тел действует сила тяжести (направлена вниз) и сила натяжения нити (направлена вверх). Когда тела опускаются в жидкости, на них дополнительно действует сила Архимеда, которая направлена вверх.
Составим условия равновесия для тел 1 и 2 в момент, когда они не были погружены в жидкости:
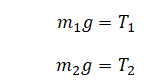
Или (выразим массу через плотность и объем, а силу натяжения 1 выразим через силу натяжения 2):

Подставим 2 выражение в 1:
![]()
Преобразовываем:
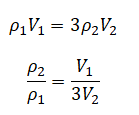
Теперь составим условие равновесия для второго случая. При этом силы натяжения нити будут уменьшены. Но так как система остается в равновесии, их соотношение останется прежним и будет равно:
![]()
Сами условия равновесия для тел 1 и 2 после погружения следующие:
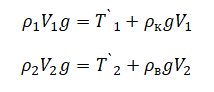
Преобразуем 1 выражение:
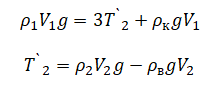
Подставим 2 выражение в 1:

Преобразуем:
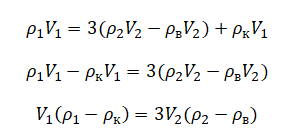
Но выше мы уже нашли, что:
![]()
Вычтем из этого выражения предыдущее и получим:
![]()
Отсюда:
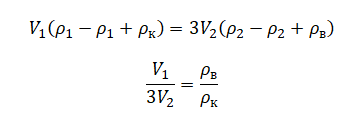
Выше уже получили, что:
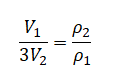
Следовательно:
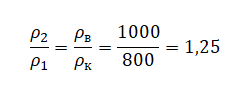
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18859
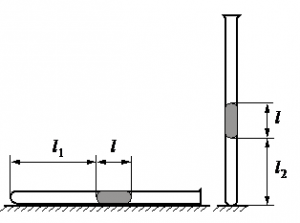 В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.
В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.
Алгоритм решения
Решение
Запишем исходные данные:
30,7 см = 30,7∙10–2 м
23,8 см = 23,8∙10–2 м
1 мм рт. ст. = 133,322 Па
747 мм рт. ст. = 99,6∙103 Па
Плотность ртути равна: ρрт = 13,54∙103 кг/м3.
Так как процесс изменения состояния газа происходит при постоянной температуре, процесс можно считать изотермическим. Для него действует газовый закон Бойля — Мариотта:
p1V1 = p2V2
Первоначальное давление на столбик воздуха равно атмосферному давлению:
p1 = pатм
Конечное давление на столбик воздуха равно сумме атмосферного давления и давления, оказываемое силой тяжести столбика ртути:
p2=pатм+mртgS
S —площадь поперечного сечения трубки.
Масса ртути равна произведению плотности на объем столбика металла. Объем в свою очередь равен произведению длины столбика ртути на площадь поперечного сечения трубки. Поэтому:
p2=pатм+ρртVртgS=pатм+ρртlSgS=pатм+ρртlg
Первоначальный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:
V1 = Sl1
Конечный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:
V2 = Sl2
Выразив первоначальные и конечный величины, можем записать закон Бойля — Мариотта применительно к данной задаче:
pатмSl1=(pатм+ρртlg)Sl2
Преобразуем уравнение, выразим искомую величину и произведем вычисления:
pатмl1=pатмl2+ρртlgl2
ρртlgl2=pатмl1−pатмl2
l=pатм(l1−l2)ρртgl2
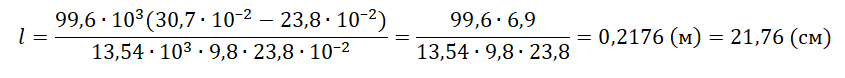
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18093
В камере, заполненной азотом, при температуре К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда
см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры
К. В результате расстояние от дна сосуда до низа пробки становится равным h (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T0. Расстояние от дна сосуда до низа пробки при этой температуре становится равным
см (см. рис. 3). Чему равно h? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь.

Алгоритм решения
Решение
Запишем исходные данные:
50 см = 0,5 м
46 см = 0,46 м
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество азота не меняется, можем принять, что:
pVT=const
Применим уравнение Менделеева — Клапейрона для всех трех состояний азота. Учтем, что
p0V0T0=p1V1T1=p2V2T2
Пусть S — площадь поперечного сечения сосуда. Тогда объемы столба азота для каждого из состояний будут равны:
V0=SL
V1=Sh
V2=SH
Известно, что в состоянии 3 температура азота поднимается до первоначальной. Поэтому уравнение Менделеева — Клапейрона примет вид:
p0SLT0=p1ShT1=p2SHT0
p0LT0=p1hT1=p2HT0
Неизвестными остались только давления. Их можно определить, записав условие равновесия пробки.
В состоянии 1 сила давления азота на пробку определяется формулой:
p0S=pатмS
В состоянии 2 на пробку действует сила давления со стороны азота и атмосферного давления, я а также сила трения, направленная вверх. Следовательно:
p1S=pатмS−Fтр=p0S−Fтр
В состоянии 3 на пробку действуют те же силы, но сила трения теперь действует не вверх, а вниз. Поэтому:
p2S=pатмS+Fтр=p0S+Fтр
Выразим из этих уравнений силу трения:
Fтр=p0S−p1S
Fтр=p2S−p0S
Приравняем правые части и получим:
p0S−p1S=p2S−p0S
Отсюда:
p0−p1=p2−p0
2p0=p2+p1
p0=p2+p12
Подставим это значение в уравнение Менделеева — Клапейрона и получим:
p2+p12LT0=p1hT1=p2HT0
Отсюда:
p2+p12L=p2H
p2L+p1L=2p2H
p1L=2p2H−p2L=p2(2H−L)
p1=p2(2H−L)L
Отсюда:
p2(2H−L)LhT1=p2HT0
Давление слева и справа взаимоуничтожается. Остается:
T0(2H−L)Lh=HT1
Отсюда выразим h:
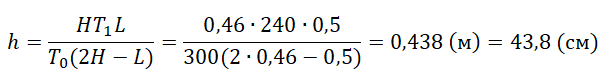
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17584
Алгоритм решения
Решение
Запишем исходные данные:
36 оС = 309 К
Относительная влажность воздуха определяется формулой:
φ=ppн100%
Давление можно выразить через уравнение состояния идеального газа:
pV=mMRT
Выразим давление:
p=mVMRT
Подставим в формулу для относительной влажности воздуха и выразим массу пара:
φ=mVMRTpн100%
m=MVφpнRT100%
Молярная масса пара равна:
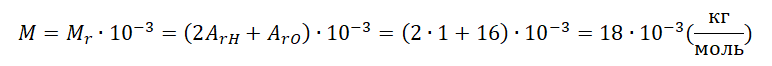
Переходим к вычислению:
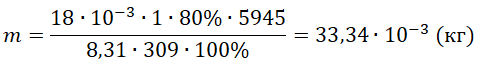
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17563
Алгоритм решения
Решение
Запишем исходные данные:
Вода при нагревании до температуры кипения получит следующее количество теплоты:
Q1=cmв(tкип−t0)
При полном сгорании дров выделится следующее количество теплоты:
Q2=λmд
Так как в окружающую среду выделится 95% тепла, то вода получит лишь 5%. Следовательно:
Q1=0,05Q2
Отсюда:
cmв(tкип−t0)=0,05λmд
mв=0,05λmдc(tкип−t0)
mв=0,05·8,3·106·1,84200(100−10)≈1,98 (кг)
Округлим ответ до целых и получим 2 кг воды.
Ответ: 2pазбирался: Алиса Никитина | обсудить разбор
Задание EF22685
В сосуде лежит кусок льда. Температура льда t1 = 0 °C. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Алгоритм решения
Решение
Запишем исходные данные:
50 кДж = 50000 Дж
333,5 кДж = 333500 Дж
Составим уравнение теплового баланса:
Qобщ=Q+q
где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:
q=Q2+Q3
Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:
Q=3λm4
Отсюда масса льда равна:
m=4Q3λ
На растопку оставшегося льда уйдет следующее количество теплоты:
Q2=λm4
На нагревание воды уйдет следующее количество теплоты:
Q3=cmt2
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Отсюда:
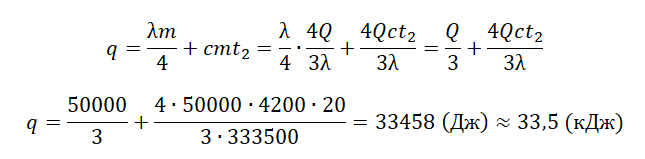
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
Решение
Запишем исходные данные:
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17724
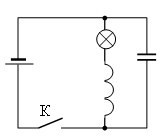 В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление источника тока соответственно равны 12 В и 1 Ом, ёмкость конденсатора 2 мФ, индуктивность катушки 36 мГн и сопротивление лампы 5 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Сопротивлением катушки и проводов пренебречь. Ответ записать в мДж.
В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление источника тока соответственно равны 12 В и 1 Ом, ёмкость конденсатора 2 мФ, индуктивность катушки 36 мГн и сопротивление лампы 5 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Сопротивлением катушки и проводов пренебречь. Ответ записать в мДж.
Алгоритм решения
Решение
Запишем исходные данные:
2 мФ = 2∙10–3 Ф
36 мГн = 36∙10–3 Гн
Пока ключ замкнут, через катушку L течёт ток определяемый внутренним сопротивлением источника и сопротивлением лампочки. Его можно вычислить, используя закон Ома для полной цепи:
I=εR+r
При этом конденсатор будет заряжен до напряжения U, которое определяется законом Ома для участка цепи:
U=IR
Подставив в это выражение закон Ома для полной цепи, получим:
U=εRR+r
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22=C2(εRR+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR+r)2
После размыкания ключа начинаются затухающие электромагнитные колебания, и вся энергия, запасённая в конденсаторе и катушке, выделится на лампе:
E=Wкон+Wкат=C2(εRR+r)2+L2(εR+r)2
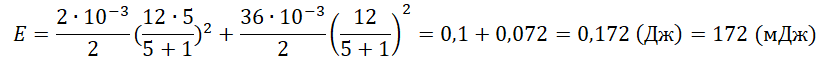
pазбирался: Алиса Никитина | обсудить разбор
👀 6.1k