Задание №23 ОГЭ по математике 🐲 СПАДИЛО.РУ

Описание задания Задача на нахождение какого либо длины или значения угла в геометрической системе.

Задание OM2407o В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6 , BC = 8 . Найдите медиану CK этого треугольника.

Алгоритм решения:

Используя св-во медианы в прямоугольном треугольнике, показываем, что искомый отрезок СК равен половине АВ.
Используя теорему Пифагора, находим АВ.
Зная АВ, вычисляем СК.

Решение:

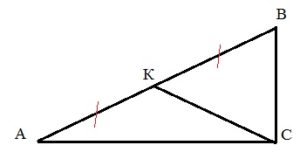
У прямоуг.треугольника есть свойство: его медиана, опущенная из вершины прямого угла на гипотенузу, равна ее половине. Поскольку ∆АВС прямоугольный, то СК=АВ/2. Это означает, что СК=АК=КВ:

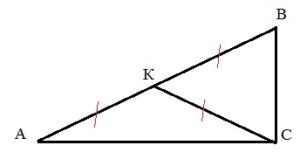
Гипотенузу АВ найдет по теореме Пифагора:

АВ²=АС²+ВС²

Отсюда:

Тогда получаем:

СК=10/2=5.

Ответ: 5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2406o Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 20, BF = 15.

Алгоритм решения:

Делаем чертеж.
Рассматриваем углы трапеции и проведенные биссектрисы.
Определяем вид треугольника AFB.
Находим длину АВ.
Записываем ответ.

Решение:

1. Выполняем рисунок, соответствующий данному условию.

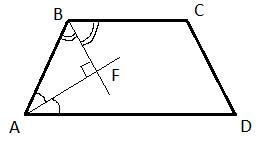
http://self-edu.ru/htm/oge2016_36/files/33_24.files/image001.jpg

2. Рассмотрим трапецию ABCD. В ней

как основания. Углы А и В составляют в сумме 180⁰, как углы при основаниях. Отсюда следует, что

как соседние при двух основаниях. По условию лучи AF и BF – биссектрисы этих углов, тогда их сумма

3. Рассматриваем треугольник ABF. В нем угол по свойству углов треугольника, т.е. построенный треугольник AFB – прямоугольный. И гипотенузой в нем является сторона AB.

4. Вычислим сторону по теореме Пифагора: АВ²= AF² + BF²

Следовательно, АВ=25.

Ответ: 25

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2405o Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 24, BF = 7.

Решение:

1. Выполняем соответствующий чертеж: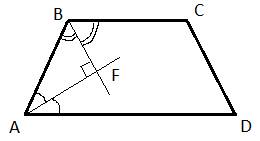

2. Трапеция ABCD имеет основаниями стороны ВС и AD, значит, они параллельны. Тогда в ней внутренние односторонние при пересечении прямых, которые содержат эти основания, секущей АВ. Следовательно, они удовлетворяют равенству: .

3. По построению, заданному условием задачи AF и BF являются биссектрисы данных углов. Тогда в треугольнике ABF

Отсюда получаем:

Таким образом, треугольник AFB прямоугольный, а сторона AB – его гипотенуза. 4. Используем теорему Пифагора: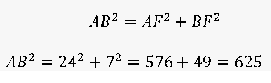

Отсюда АВ=25.

Ответ: 25

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2404o Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 24, BF = 18.

Алгоритм решения:

Делаем чертеж.
Рассматриваем углы трапеции и проведенные биссектрисы.
Определяем вид треугольника AFB.
Находим длину АВ.
Записываем ответ.

Решение:

1. Выполняем рисунок, согласно требованиям задачи:

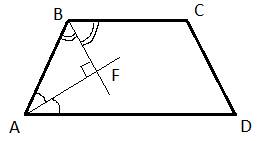
2. У трапеции ABCD стороны AB и CD основания, значит, они параллельны. Прямая АВ является секущей параллельных прямых, которые содержат основания. Следовательно,

, поскольку они являются внутренними односторонними. По построению AF и BF являются биссектрисами внутренних односторонних углов. Тогда сумма углом BAF и FBA определяется так:

3. Тогда в треугольнике ABF угол AFB равен:

∠ AFB =180⁰—(∠BAF —∠FBA)= 180⁰ – 90⁰

Таким образом, треугольник AFB является прямоугольным, причем AB – гипотенуза 4. Воспользуемся теоремой Пифагора для ее вычисления:

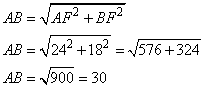
http://self-edu.ru/htm/oge2016_36/files/33_24.files/image006.gif

Ответ: 30

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2403o Углы B и C треугольника ABC равны соответственно 66° и 84°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 15.

Алгоритм решения:

Делаем чертеж по условию задания.
Определяем угол А.
Используем следствие из теоремы синусов для треугольника АВС.
Определяем ВС.
Записываем ответ.

Решение:

1. Делаем чертеж, соответствующий условию задания.

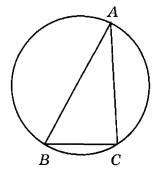
http://self-edu.ru/htm/2018/oge2018_36/files/1_24.files/image001.jpg

2. Найдем угол А треугольнике ABC:

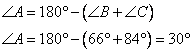
3. Радиус R описанной окружности вокруг треугольника связан с длиной BC и синусом угла A выражением, которое является следствием теоремы синусов:

Отсюда получаем:

Ответ: 15

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2402o Углы В и С треугольника ABC равны соответственно 72° и 78°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 17.

Алгоритм решения:

Делаем чертеж по условию задания.
Находим угол А в треугольнике.
Используем следствие из теоремы синусов для треугольника АВС.
Определяем ВС.
Записываем ответ.

Решение:

1. Делаем чертеж, удовлетворяющий условию задачи.

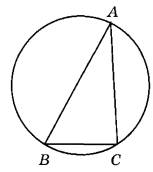
2. Рассматриваем треугольник ABC. В нем определяем угол A: ∠А=180⁰—∠В —∠С, откуда ∠А=180⁰ —71⁰—79⁰= 30⁰. 3. По теореме синусов и следствию из нее:

где R – радиус описанной окружности. Имеем:

4. Определяем ВС из полученного равенства:

Ответ: 17

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2401o Углы В и С треугольника ABC равны соответственно 71° и 79°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 8.

Алгоритм решения:

Делаем чертеж по условию задания.
Находим угол А в данном треугольнике.
Используем следствие из теоремы синусов для треугольника АВС
Определяем ВС.
Записываем ответ.

Решение:

1. Делаем чертеж, удовлетворяющий условию задачи.

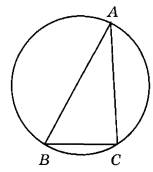
2. Определим угол А: ∠А=180⁰ —71⁰—79⁰= 30⁰. 3. Пусть R — радиус описанной окружности, тогда по следствию из теоремы синусов получаем:

4. Тогда, при подстановке в равенство полученных данных, получаем: ВС равно произведению сторон АВ и АС на синус угла А, который равен 30⁰. Следовательно ВС=2∙8∙0,5=8.

Ответ: 8

pазбирался: Даниил Романович | обсудить разбор | оценить

Ирина | 👀 10.5k | 📄 Скачать PDF |

5 комментариев

Влад Гречко
03.06.2017 at 15:13 Ответить
супер
____
08.12.2017 at 15:44 Ответить
все хорошо, но я не поняла как сначала раскрыть скобки
- Даниил
  08.12.2017 at 16:30 Ответить
  Как разложить биквадратное уравнение на множители? Напишите чуть конкретнее, поможем!
.......
16.12.2017 at 00:03 Ответить
почему точки -4 и 6 — выколоты?
- Даниил
  16.12.2017 at 00:40 Ответить
  Тут имеется в виду координата точки — ( -2; -4) -2 по оси икс, -4 — по оси игрек. И аналогично со второй точкой. По оси икс выколоты только две, которые обращают знаменатель в ноль. Согласен, что не сразу понятно, скоро мы перепишем раздел, будет больше примеров и подробный разбор, спасибо за отклик!

Задание №23 ОГЭ по математике

геометрические задачи на вычисление

Алгоритм решения:

Решение:

Алгоритм решения:

Решение:

Алгоритм решения:

Решение:

Алгоритм решения:

Решение:

Алгоритм решения:

Решение:

Алгоритм решения:

Решение:

Алгоритм решения:

Решение:

5 комментариев

Добавить комментарий Отменить ответ