ОГЭ 2021 по математике: разбор реального варианта
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Разбираем реальный вариант ОГЭ по математике 2021 года.
Задание 25OM21R
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
AEAB=ABAF откуда по свойству пропорции АВ2=АЕ∙АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
AEAD=ACAF ; откуда выразим AD=AE∙AFАC=AE∙AFAC
Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC
Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD=AE∙AFAC=36254=24
Теперь найдем CD=AC-AD=54-24=30
Ответ: 30pазбирался: Базанов Даниил | обсудить разбор
Задание 24OM21R
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 23OM21R
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 300 и 1350, а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=900, следовательно, треугольник прямоугольный. Найдем величину угла DCН, 1350 – 900=450 (так как провели высоту CН). Отсюда следует, что угол D=450, так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а√2, где с=17. Следовательно, CН =17√2=17√22.
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН=17√22. Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2×17√22=17√2
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 22OM21R
у=х2 - |2x +1|
Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки.Раскроем модуль:
{у=х2−2х−1, при х≥−12у=х2+2х+1, при х<−12)
Для построения графика найдем вершины каждой параболы:
у=х2 – 2х – 1
х0=−b2a=22=1
у0=12 -2-1=-2
Итак, вершина первой параболы (1; -2)
Возьмем дополнительные точки, где х ≥−12
| х | -0,5 | 0 | 2 | 3 |
| у | 0,25 | -1 | -1 | 2 |
у=х2 + 2х + 1
Аналогично найдем вершину второй параболы: х0=-1, у0=0
Вершина второй параболы (-1;0)
Дополнительные точки при х<−0.5
| х | -2 | -0,5 |
| у | 1 | 0,25 |
Изобразим параболы в системе координат:
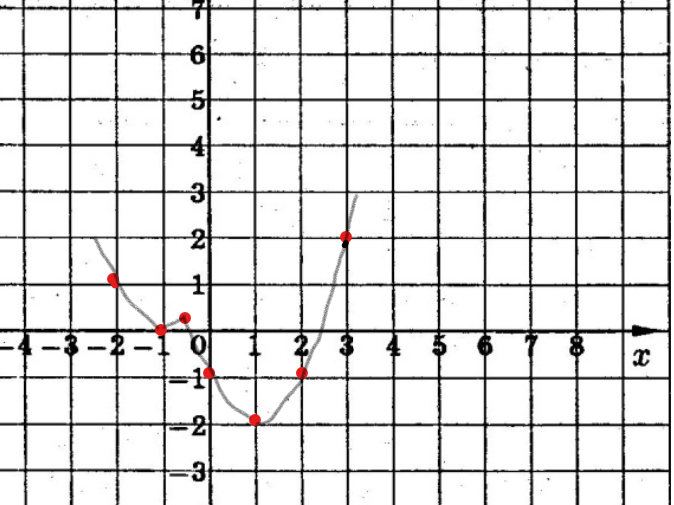
Теперь нам нужно ответить на вопрос задания: «Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки?»
Для этого построим такие прямые (одна желтая, вторая зеленая), откуда видно, что первая прямая совпадает с осью х, т.е. у=0; вторая имеет с графиком три общие точки при у=0,25.
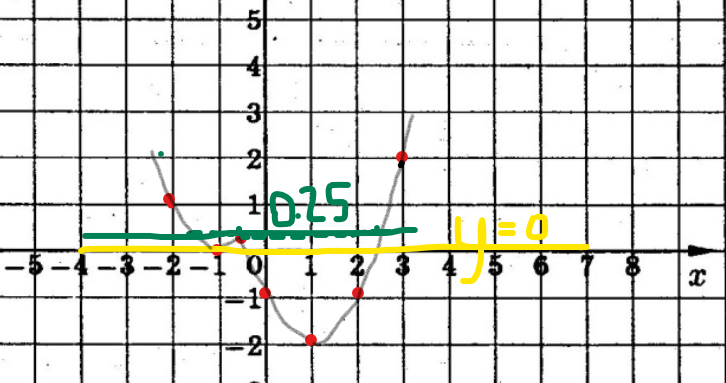
Ответ: при m равных 0; 0,25
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
Задание 21OM21R
Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:
| Скорость | Время | Расстояние | |
| 1 автомобиль | х | 800х | 800 |
| 2 автомобиль | х — 36 | 800х−36 | 800 |
Пояснения к заполнению таблицы:
Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.
Расстояние у каждого авто будет 800 км.
Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.
Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:
800х−36− 800х=5
Приведем к общему знаменателю х(х-36) наше уравнение и решим его:
800х – 800(х-36)=5х(х-36)
800х – 800х+28800=5х2 – 180
28800=5х2 – 180
5х2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:
х2 – 36 – 5760=0
Решим полученное квадратное уравнение
D=b2 – 4ac=362 — 4∙(−5760)=24336
х1,2=−b±√D2a=36±1562
Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.
Значит, скорость первого автомобиля 36 км/ч
Ответ: 36pазбирался: Базанов Даниил | обсудить разбор
Задание 20OM21R
Нам дано уравнение третьей степени: х3 + 6х2=4х + 24
В данном уравнении перенесем все слагаемые в одну сторону ( в левую), изменяя при этом знаки: х3 + 6х2 – 4х – 24=0
Теперь сгруппируем слагаемые: (х3 + 6х2) – (4х + 24)=0
Вынесем общий множитель за скобки из каждой группы: х2(х + 6) – 4(х + 6)=0
Вынесем за скобки выражение (х + 6): (х + 6)(х2– 4)=0
Приравняем каждый множитель к нулю и решим полученные уравнения:
х + 6=0 и х2– 4=0
х=-6 и х2=4, отсюда х1,2=±2
Ответ: 2pазбирался: Базанов Даниил | обсудить разбор
Задание 19OM21R
- Сумма углов равнобедренного треугольника равна 180 градусам.
- Боковые стороны любой трапеции равны.
- Центры вписанной и описанной окружностей треугольника совпадают.
Обращаем внимание на то, что вопрос содержит слово КАКИЕ, что означает нахождение нескольких верных ответов. Итак, первое утверждение является верным, потому что есть теорема о сумме углов треугольника, равной 180 градусов, это не зависит от вида треугольника. Второе утверждение является не верным, так как по определению, только у равнобедренной трапеции боковые стороны равны. Теперь становится понятным, что третье утверждение тоже должно быть верным. Но в доказательство тому мы имеем правила, которые нам говорят о том, что центры окружностей совпадают.
Итак, наши верные утверждения под номерами 1 и 3.
Ответ: 13pазбирался: Базанов Даниил | обсудить разбор
Задание 18OM21R
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4pазбирался: Базанов Даниил | обсудить разбор
Задание 17OM21R
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула
S=a+b2h, для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S=7+112∙7=182∙7=9∙7=63
Ответ: 63pазбирался: Базанов Даниил | обсудить разбор
Задание 16OM21R
Радиус вписанной в квадрат окружности равен 22√2. Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22√2, то сторона квадрата будет в два раза больше, т.е. 44√2.
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44√2. Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а√2, где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44√2×√2=44√4=44×2=88
Ответ: 88pазбирался: Базанов Даниил | обсудить разбор
Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42pазбирался: Базанов Даниил | обсудить разбор
Задание 14OM21R
Можно решить данную задачу логическим путем, т.е. без формулы. Так как начальная температура была -6, а потом уменьшалась на 8 градусов в течение 6 минут, то можно сделать следующее:
-6-8=-14 через 1 минуту
-14-8=-22 через 2 минуты
-22-8=-30 через 3 минуты
-30-8=-38 через 4 минуты
-38-8=-46 через 5 минут
-46-8=-54 через 6 минут
Значит, наш ответ -540С
Вторым способом является решение по формуле n-ого члена арифметической прогрессии, которая есть также и в справочном материале, т.е. an=a1+d(n – 1). В данном случае a1=-6; d=-8, n=7 (так как ЧЕРЕЗ 6 минут). Подставим значения в формулу: a7=-61-8(7 – 1). Вычислим: a6=-6-8∙5=-6-48=-54.
Ответ: -54pазбирался: Базанов Даниил | обсудить разбор
Задание 13OM21R
- [0; +∞)
- [8; +∞)
- [0; 8]
- (-∞;0]∪[8;+∞)
8х – х2≥0
Вынесем -х за скобки: -х(-8 + х) ≥0
Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – 8) ≤0
Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.
Итак, имеем нули функции 0 и 8.
Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.
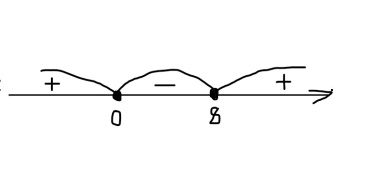
Теперь находим промежуток чисел, соответствующий неравенству х(х – 8) ≤0, т.е. промежуток отрицательных или равных нулю чисел. Это будет промежуток [0; 8]
В соответствии с его номером, это будет ответ под №3.
Ответ: 3pазбирался: Базанов Даниил | обсудить разбор
Задание 12OM21R
Площадь четырехугольника можно вычислить по формуле S=d1d2sina2, где d1 и d2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2=16, sin a=25, a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8=d1×16×252
В правой части можно сократить 16 и 2 на 2: 12,8=d1×8×251
Теперь умножим 8 на дробь 25, получим 3,2: 12,8=d1×3,2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d1=12,8:3,2=4
Ответ: 4pазбирался: Базанов Даниил | обсудить разбор
Задание 11OM21R
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
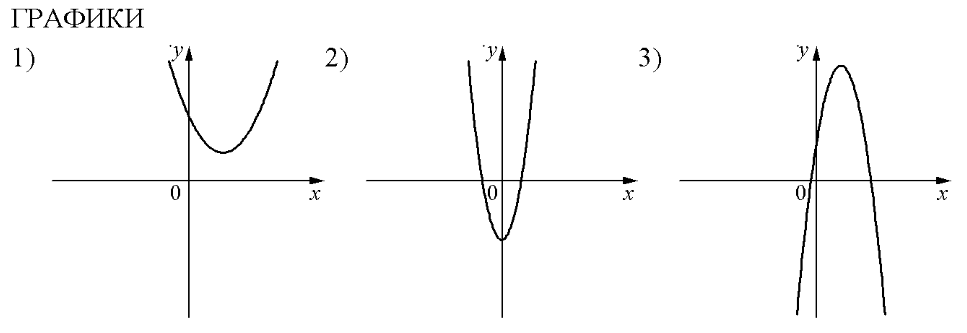 В таблице под каждой буквой укажите соответствующий номер.
Ответ:
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
| А | Б | В |
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
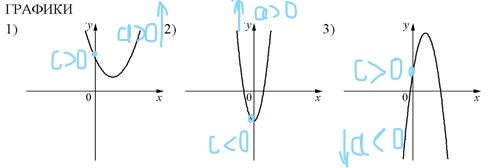
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 — это график №1
Б) а<0; с>0 — это график №3
В) а>0, с<0 – это график №2
| А | Б | В |
| 1 | 3 | 2 |
pазбирался: Базанов Даниил | обсудить разбор
Задание 10OM21R
Это задача на простую вероятность, где надо знать число благоприятных исходов и разделить его на общее количество.
Так как нам надо найти вероятность, что фонарик будет исправным, то 100 – 9=91 – это количество исправных фонариков (по условию их всего 100 и из них 9 неисправных).
Для нахождения вероятности надо разделить число благоприятных исходов (в нашем случае – это 91) на общее количество фонариков – на 100. Итак, 91:100=0,91. Значит, вероятность того, что выбранный наудачу в магазине фонарик окажется исправен, равна 0,91.
Ответ: 0,91pазбирался: Базанов Даниил | обсудить разбор
Задание 9OM21R
Имеем линейное уравнение:
2 + 3х= – 7х – 5
Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.
Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.
Запись решения выглядит так:
2 + 3х= – 7х – 5
3х + 7х= – 5 – 2
10х= –7
х=–7:10
х=–0,7
Ответ: –0,7pазбирался: Базанов Даниил | обсудить разбор
Задание 8OM21R
(3∙8)737∙85
В числителе дроби возведем в степень каждый множитель:
(3∙8)737 ∙85=37∙8737∙85
Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.
(3∙8)737 ∙85=37∙8737∙85=82=64
Ответ: 64pазбирался: Базанов Даниил | обсудить разбор
Задание 7OM21R
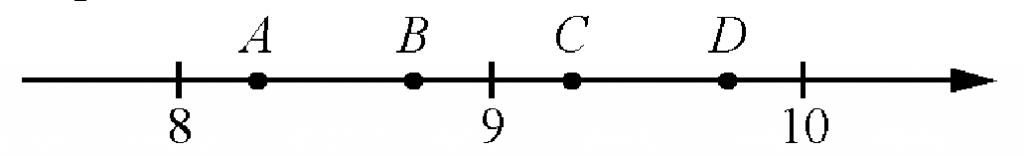 Одна из них соответствует числу 10713. Какая это точка?
Одна из них соответствует числу 10713. Какая это точка?
- точка А
- точка В
- точка С
- точка D
Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А.
Ответ: 1pазбирался: Базанов Даниил | обсудить разбор
Задание 6OM21R
Выполним вычитание десятичных дробей, где 9,4 больше по модулю, значит, ответ будет отрицательным. Итак, – (9,4 – 4,9)= – 4,5
Ответ: -4,5pазбирался: Базанов Даниил | обсудить разбор
Задание 15OM21R

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Ответ: 11
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Ответ: 4
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Ответ: 48
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер
магазина |
Расход
краски |
Масса краски
в одной банке |
Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: 30500
Ответ: см. решениеpазбирался: Базанов Даниил | обсудить разбор
👀 16k