Задание №28 ЕГЭ по физике
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 1 мин.
Условие задания № 28 может быть связано с любым разделом физики. Основное условие: необходимость использования при его решении одного или нескольких фундаментальных физических законов.
Задание ЕГЭ-Ф-ДВ2023-28
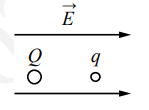 В однородном электрическом поле с напряжённостью E =18 В/м находятся два точечных заряда: Q = −1 нКл и q = +5 нКл с массами M = 5 г и m =10 г соответственно (см. рисунок). На каком расстоянии d друг от друга находятся заряды, если их ускорения совпадают по величине и направлению? Сделайте рисунок с указанием всех сил, действующих на заряды. Силой тяжести пренебречь.
В однородном электрическом поле с напряжённостью E =18 В/м находятся два точечных заряда: Q = −1 нКл и q = +5 нКл с массами M = 5 г и m =10 г соответственно (см. рисунок). На каком расстоянии d друг от друга находятся заряды, если их ускорения совпадают по величине и направлению? Сделайте рисунок с указанием всех сил, действующих на заряды. Силой тяжести пренебречь.Алгоритм решения:
Решение:
Запишем исходные данные:
Переведем единицы измерения в СИ:
Q = –1 нКл = –10–9 Кл
q = +5 нКл = +5∙10–9 Кл
M = 5 г = 5∙10–3 кг
m = 10 г = 10–2 кг
Сделаем поясняющий рисунок:
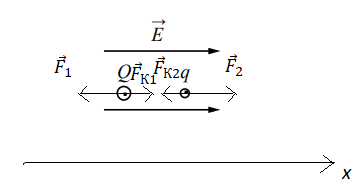
На точечный заряд Q действует 2 силы. Первая сила — →F1 — это электрическая сила, действующая со стороны однородного поля. Она направлена противоположно силовым линиям этого поля, так как этот заряд отрицательный. Вторая сила — →FК1 — это сила Кулона, действующая со стороны второго заряда. Так как заряды разноименные, то эта сила направлена в сторону второго (положительного) заряда.
На точечный заряд q тоже действует 2 силы. Первая сила — →F2 — это электрическая сила, действующая со стороны однородного поля. Она направлена по направлению силовых линий этого поля, так как этот заряд положительный. Вторая сила — →FК2 — это сила Кулона, действующая со стороны первого заряда. Так как заряды разноименные, то эта сила направлена в сторону второго (отрицательного) заряда.
Запишем формулы для определения модулей сил, действующих на каждый из этих зарядов:
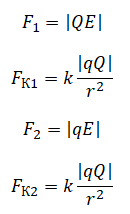
Видно, что силы Кулона 1 и 2 равны по модулю:
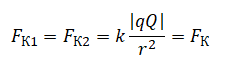
Равнодействующая сил, действующих на заряд Q, равна разности силы Кулона 1 и силы со стороны однородного поля на этот заряд. Согласно 2 закону Ньютона, равнодействующая сил равна произведению массы на ускорение. Следовательно:
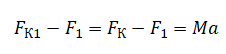
Для второго заряда запишем аналогично (учитываем направление сил):
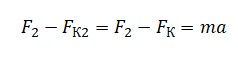
Выразим из обоих выражений ускорения. Так как по условию они равны, приравняем правые части уравнений:
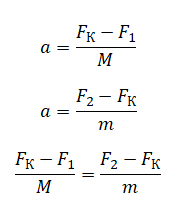
Теперь подставим в эту формулу выражения, полученные для модулей каждой из сил:
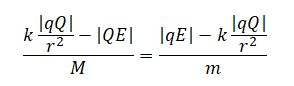
Выразим отсюда r путем следующих преобразований:
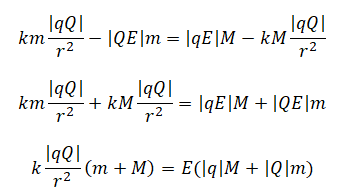
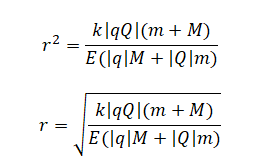
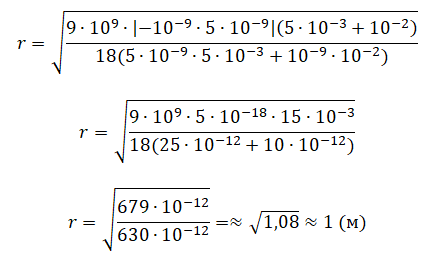
.
Ответ: 1pазбирался: Алиса Никитина | обсудить разбор
Задание EF17717
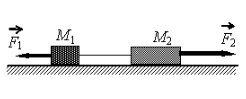 Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы F1 и F2, как показано на рисунке. Сила натяжения нити Т = 15 Н. Каков модуль силы F1, если F2 = 21 Н?
Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы F1 и F2, как показано на рисунке. Сила натяжения нити Т = 15 Н. Каков модуль силы F1, если F2 = 21 Н?
а) 6 Н
б) 12 Н
в) 18 Н
г) 21 Н
Алгоритм решения
Решение
Запишем исходные данные:
Сделаем чертеж. Систему координат выберем такую, чтобы ось ОУ была параллельная ускорению свободного падения.
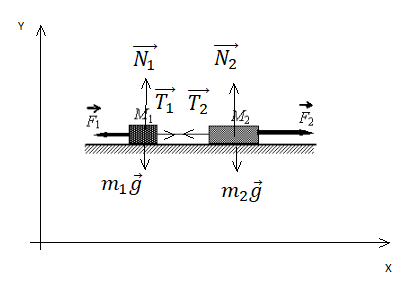
Согласно третьему закону Ньютона, два тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Поэтому модули сил натяжения нити Т1 и T2 равны:
T1 = T2 = T
Учтем это при записи второго закона Ньютона для каждого из тел:
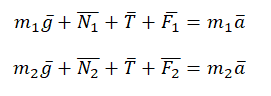
Запишем второй закон Ньютона в проекциях на оси ОХ и ОУ. Сначала для первого тела:
T – F1 = m1a
N1 = m1g
Теперь для второго тела:
F2 – T = m2a
N2 = m2g
Выразим из проекции на ось ОХ для 1 тела модуль первой силы:
F1 = T – m1a
Из проекции на ось ОХ для второго тела выразим ускорение:
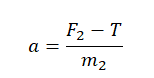
Подставим ускорение в формулу для нахождения силы, действующей на первое тело:
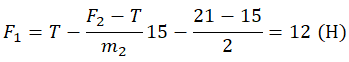
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17647
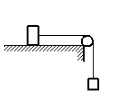 По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
а) 2,25 Н
б) 2,7 Н
в) 3 Н
г) 3,6 Н
Алгоритм решения
Решение
Запишем исходные данные:
Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.
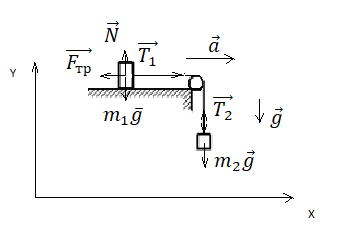
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:
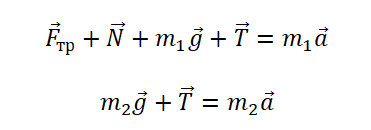
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:
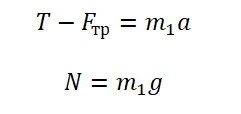
Запишем проекцию на ось ОУ для груза на нити:
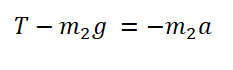
Выразим из этого выражения ускорение и получим:
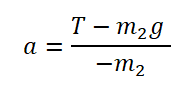
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:
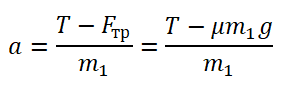
Приравняем правые части уравнений и получим:
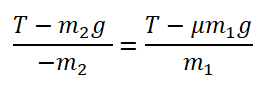
Произведем вычисления:

Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
 Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.Алгоритм решения
Решение
Запишем исходные данные:
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6pазбирался: Алиса Никитина | обсудить разбор
Задание EF22698
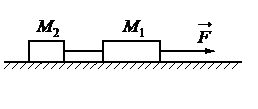 Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?
Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?Алгоритм решения
Решение
Запишем исходные данные:
Выполним чертеж:
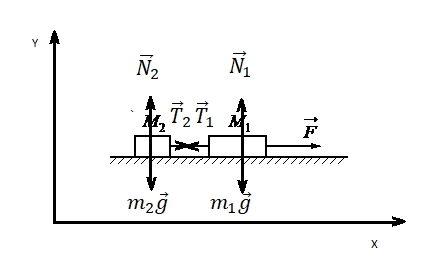
Запишем второй закон Ньютона для 1 и 2 тела соответственно:
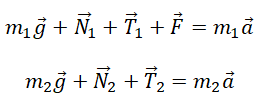
Запишем второй закон Ньютона для 1 и 2 тела в проекции на ось ОХ:
F – T1 = m1a
T2 = m2a
Отсюда масса второго тела равна:
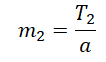
Согласно третьему закону Ньютона, тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Следовательно, силы натяжения нити равны на обоих концах:
T1 = T2 = T
Поэтому:
T = F – m1a
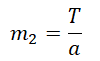
Из первого выражения выразим ускорение и подставим его во второе:
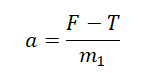
Подставим в формулу и получим:
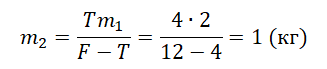
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18192
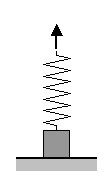 К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.
К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.
Ответ:
а) 40 мДж
б) 20 мДж
в) 80 мДж
г) 200 мДж
Алгоритм решения
Решение
Запишем исходные данные:
Переведем сантиметры в метры:
2 см = 0,02 м
Выполним рисунок. Для описания ситуации нам понадобится только одна ось: Oy.
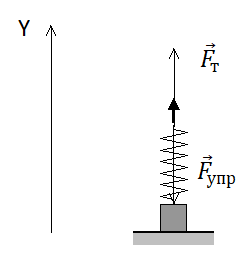
Потенциальная энергия деформированной пружины определяется формулой:
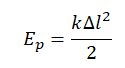
Так как брусок поднимают за прикрепленную к нему пружину медленно, можно считать, что это движение равномерное (и прямолинейное). Поэтому, согласно второму закону Ньютона:
Fт = Fупр
Чтобы оторвать брусок от поверхности стола, модуль силы тяги должен быть равен модулю силы тяжести. Поэтому:
Fт = Fтяж =Fупр
Или:
mg = k∆l
Теперь можем выразить жесткость пружины:
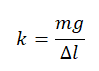
Подставим жесткость пружины в формулу потенциальной энергии и сделаем вычисления:
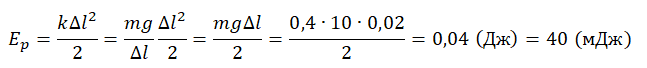
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18087
Шайба массой m, скользящая по гладкой горизонтальной поверхности, налетает на лежащую неподвижно на той же поверхности шайбу массой 3m такого же размера. После частично неупругого удара первая шайба остановилась. Какова была кинетическая энергия первой шайбы до удара, если при ударе выделилось количество теплоты Q?
Ответ:
а) 3Q/2
б) 2Q
в) 9Q/2
г) 8Q
Алгоритм решения
Решение
Запишем исходные данные:
До удара двигалась только первая шайба, вторая покоилась, поэтому импульс второй шайбы равен нулю. После удара первая шайба остановилась, поэтому ее импульс стал равен нулю. Но начала двигаться вторая шайба. Поэтому закон сохранения импульса при ударе примет вид:
mv=3mV
Отсюда скорость второй шайбы равна v/3.
Запишем закон сохранения энергии с учетом того, что при ударе выделилось тепло:
Ek1=Ek2+Q
Кинетическую энергию второй шайбы можно выразить как доля от кинетической энергии первой шайбы, а также как произведение половинной массы на половинный квадрат:
Ek2=Ek1x=3mV22=3mv22·9
x — доля кинетической энергии второй шайбы от кинетической энергии первой шайбы.
Кинетическая энергия первой шайбы равна:
Ek1=mv22
Теперь можем выразить x:
3mv22·9=mv22x
x=13
Следовательно, на кинетическую энергию второй шайбы ушла 1/3 часть кинетической энергии первой шайбы, а в виде тепла выделилось 2/3 этой энергии. Отсюда:
Q=23Ek1
Ek1=32Q
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
Решение
Запишем исходные данные:
Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17982
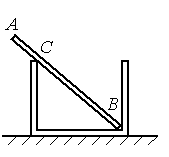 Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
Ответ:
а) 0,3 Н
б) 0,25 Н
в) 0,6 Н
г) 0,13 Н
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Выполнить чертеж. Выбрать ось вращения. Указать силы и их плечи.
- Использовать второй и третий законы Ньютона, чтобы выполнить общее решение.
- Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Масса стержня: m = 100 г.
- Модуль силы, с которой стержень давит на стенку сосуда в точке С: FC = 0,5 Н.
- Модуль вертикальной составляющей силы, с которой стержень давит на сосуду в точке В: FBy = 0,6 Н.
Переведем единицы измерения в СИ:
100 г = 0,1 кг
Выполним чертеж:

Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы:
- сила тяжести (mg);
- сила реакции опоры в точке С (FC);
- сила реакции опоры в точке В (FВ).
Поэтому:
m→g+→FC+→FB=0
Запишем проекции на оси Ox и Oy соответственно:
FCx=FBx
FCy+FBy=mg
Модуль горизонтальной составляющей силы в точке В можно выразить через теорему Пифагора:
FCx=√F2C−F2Cy
Но вертикальная составляющая силы в точке C равна разности силы тяжести и горизонтальной составляющей силы в точке В:
FCy=mg−FBy
Отсюда:
FBx=FCx=√F2C−F2Cy=√F2C−(mg−FBy)2
Подставим известные данные и вычислим:
FBx=√0,52−(0,1·10−0,6)2=√0,25−0,16=0,3 (Н)
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Алгоритм решения
Решение
Анализируя условия задачи, можно выделить следующие данные:
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
Алгоритм решения
Решение
Анализируя условия задачи, можно выделить следующие данные:
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2pазбирался: Алиса Никитина | обсудить разбор
Задание EF17512
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд – со вторым, второй – с третьим. Первоначально давление газа в сосудах было равно соответственно р, 3р и р. В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
Алгоритм решения
Решение
Запишем исходные данные:
После того, как открыли кран между 2 и 3 сосудом, объем возрос вдвое, и давление распределилось по нему равномерно. Согласно закону Дальтона, оно стало равным сумме давлений, оказываемых газами в количестве вещества ν2 и ν3. Так как объем после открытия крана увеличивается вдвое, то парциальное давление каждого из количества вещества равно половине исходного давления:
p23=p2+3p2=2p
Потом кран 2–3 закрыли, но открыли кран 1–2. Применим закон Дальтона, получим:
p12=2p2+p2=3p2
Теперь применим закон Менделеева — Клапейрона:
pV=νRT
Для начального состояния газа в 1 сосуде:
pV=ν1RT
Для конечного состояния газа в 1 сосуде:
3p2V=ν2RT
Так как температура и объем неизменны, но давление увеличилось в 1,5 раза, то и количество газа в первом сосуде увеличилось в 1,5 раза.
Ответ: Увеличилосьpазбирался: Алиса Никитина | обсудить разбор
Задание EF17579
При постоянном давлении гелий нагрели, в результате чего он совершил работу 5 кДж? Масса гелия 0,04 кг. Насколько увеличилась температура газа?
Ответ:
а) 60 К
б) 25 К
в) 15 К
г) 3 К
Алгоритм решения
Решение
Запишем исходные данные:
5 кДж = 5000 Дж
Первое начало термодинамики:
ΔU=Q+A
Учтем, что не над газом совершают работу, а сам газ совершает ее:
Отсюда:
ΔU=Q−A
Так как газ нагревали изобарно, часть тепла ушла на изменение внутренней энергии газа, а часть — на совершение этим газом работы.
Работа, совершенная газом, равна:
A=pΔV=mMRΔT
Молярная масса гелия равна 4∙10–3 кг/моль.
Отсюда:
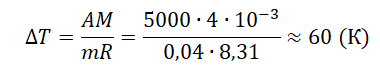
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17648
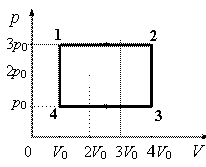 За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Qнагр = 5,1кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1–2 газ совершает работу
За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Qнагр = 5,1кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1–2 газ совершает работу
Ответ:
а) 1,2 кДж
б) 1,8 кДж
в) 2,6 кДж
г) 3,9 кДж
Алгоритм решения
Решение
Запишем исходные данные:
5,1 кДж = 5,1∙103 Дж
Согласно графику, на участке 1–2 газ совершает работу, равную:
A=3p0(4V0−V0)=9p0V0
Полезная работа ограничивается площадью фигуры внутри циклического графика. Она равна:
Aползн=9p0V0−p0(4V0−V0)=6p0V0
Отсюда:
A=9Aползн6
КПД тепловой машины есть отношение полезной работы к количеству теплоты, полученному от нагревателя:
η=AползнQ
Отсюда:
Aползн=ηQ
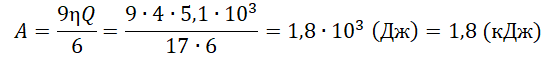
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17508
Смещение груза пружинного маятника меняется с течением времени по закону x=Acos2πTt, где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника вернется к своему исходному значению?
Ответ:
а) 0,1 с
б) 0,2 с
в) 0,3 с
г) 0,5
Алгоритм решения
Решение
Известно, что смещение маятника меняется по закону:
x=Acos2πTt
В начальный момент времени t = 0 смещение будет равно амплитуде, поскольку косинус нуля равен «1». Следовательно, исходное значение потенциальной энергии маятника равно:
Wp0=kA22
Сделаем рисунок, обозначив за x0 положение равновесия системы. Тогда A и –A будут амплитудами (максимальными смещениями от положения равновесия).
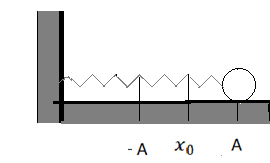
Потенциальная энергия зависит только от модуля смещения, поэтому ее значение станет таким же, как в начальный момент времени, когда смещение достигнет максимального смещения с противоположной стороны (оно составит –A). В этом легко убедиться:
Wpt=k(−A)22=kA22=Wp0
К этому моменту пройдет половина периода колебания, следовательно:
t=T2=12=0,5 (с)
Ответ: гpазбирался: Алиса Никитина | обсудить разбор
Задание EF17581
В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора в первом контуре.
Ответ:
а) 1 мкКл
б) 4 мкКл
в) 6 мкКл
г) 9 мкКл
Алгоритм решения
Решение
Запишем исходные данные:
6 мкКл = 6∙10–6 Кл
Амплитудные значения силы тока и заряда конденсатора связываются формулой:
Imax=qmax 2πT
Запишем эту формулу для первого и второго колебательного контура:
I1max=q1max 2πT1
I2max=q2max 2πT2
Преобразуем их, оставив слева только 2π:
2π=I1maxT1q1max=ITq1max
2π=I2maxT2q2max=2I3Tq2max=6IT6·10−6=IT10−6
Поскольку левые части уравнений равны, мы можем приравнять их правые части:
ITq1max=IT10−6
Следовательно, q1max=10−6 Кл.
Ответ: аpазбирался: Алиса Никитина | обсудить разбор
Задание EF18697
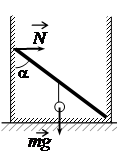 Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N, действующей на стержень со стороны левой стенки ящика?
Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N, действующей на стержень со стороны левой стенки ящика?
Алгоритм решения
Решение
Запишем исходные данные:
Чтобы записать правило моментов, нужно определить плечи силы тяжести и силы упругости. В качестве точки равновесия выберем точку опоры нижнего конца стержня. Тогда плечо силы тяжести будет равно произведению половины длины стержня на косинус угла между дном ящика и стержнем. Он тоже будет равен 45 градусам, так как он равен разности 180 градусов и угла α = 45o. Отсюда:
dmg=l2cosα
Плечо силы упругости будет равно расстоянию от дна ящика до верхней точки стержня. Оно определяется как произведение длины стержня на синус угла α:
dN=lsinα
Запишем правило моментов:
mgl2cosα=Nlsinα
Отсюда:
N=mgl2lsinαcosα
Длина стержня в числителе и знаменателе сократится, косинус и синус угла тоже, так как при 45 градусах они одинаковые. Следовательно:
N=mg2=1·102=5 (Н)
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Алгоритм решения
Решение
Запишем исходные данные:
Ускорение свободного падения определяется формулой:
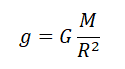
Отсюда радиус равен:
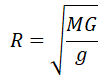
Линейная скорость и радиус орбиты связываются формулой:
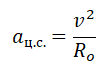
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
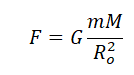
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
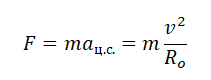
Отсюда:
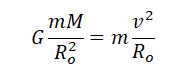
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
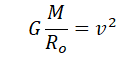
Из этой формулы выразим массу планеты:
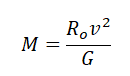
Подставим массу планеты в формулу для нахождения ее радиуса:
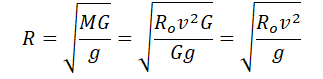
Подставляем известные данные и вычисляем:
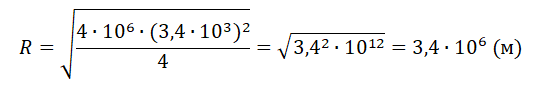
Этот радиус соответствует 3400 км.
Ответ: 3400pазбирался: Алиса Никитина | обсудить разбор
👀 5.5k