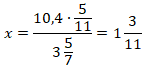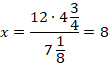Для обозначения отношения чисел используется знак деления «:» либо черта дроби.
Общая форма записи отношения чисел: a : b или, соответственно
![]()
В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: b≠0.
Свойства отношений
Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.
Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.
Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.
В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта. При этом под абсолютными величинами понимают величины, выраженные в конкретных единицах измерения – кг, км и так далее.
Процентное отношение
Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.
Математическая запись:
![]()
Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.
Пример. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?
Обозначим искомую величину через х. Тогда получаем:
Пример. Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?
Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:
Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:
![]() Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.
Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.
Специальной единицы измерения доля не имеет и измеряется просто в единицах.
Пример. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?
Обозначим искомую величину через х. Составим отношение и найдем х:
![]()
Переход от долей к процентам предельно прост: достаточно умножить долю на 100. Так, в предыдущем примере 0,683 по отношению к общему тиражу составит 0,683×100%=68,3% .
Пример. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?
Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:
![]()
Пропорция
Примеры конкретных пропорций:
![]()
![]()
![]()
При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.
Пример:
Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:
Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.
Пример. Дана пропорция:
Требуется найти х.
Пример. Дана пропорция:
Необходимо найти х.