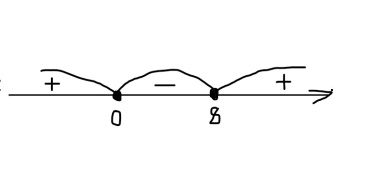
Для решения данного вида неравенств используется свойство чередования знаков функции f(x)=(х – х1)(х – х2)….(х – хn), где числа х1, х2, …, хn называются нулями функции. Эти нули функции разбивают область определения (она представляет собой любое число, т.е. промежуток чисел от минус бесконечности до плюс бесконечности) на промежутки, в каждом из которых знак функции сохраняется, а при переходе через нуль ее знак изменяется. Данные промежутки называют интервалами, а решение неравенств данным способом – методом интервалов.
Для начала решения неравенство должно быть представлено в стандартном виде. Рассмотрим решение такого вида неравенств методом интервалов на примерах.
Пример №1. Решить неравенство:
(х–1)(х+5)(х–8)>0
Найдем нули функции: для этого возьмем из каждой скобки данные числа с противоположными знаками, поэтому имеем х1=1, х2=–5, х3=8. Данные числа разбивают область определения на промежутки (−∞;−5);(−5;1);(1;8);(8;+∞). Удобно показать их на координатном луче, помня о том, что неравенство по условию строгое, значит, точки будут «выколотые»:
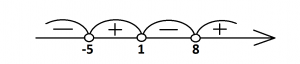
Теперь посмотрим, как расставить знаки в промежутках. Начнем справа, возьмем из этого промежутка любое число, например, 9 и подставим его в наше неравенство:
(9–1)(9+5)(9–8)=8×14×1>0,
то есть получили, что произведение – положительное число, поэтому ставим знак «плюс»; теперь берем число из промежутка (1;8), например, 5 и также подставим в неравенство для определения знака произведения:
(5–1)(5+5)(5–8)=4×10×(–3)<0
Значит, ставим в данном промежутке знак «минус». Также поступаем со следующим промежутком, возьмем число 0, подставим и получим, что произведение будет положительным, ставим знак «плюс». И аналогично ищем знак последнего промежутка, он будет «минус». Из рисунка видно, что знаки чередуются, поэтому надо запомнить, чтобы не проверять знак каждого промежутка, можно просто справа налево расставить знаки чередованием, начиная со знака «плюс». Для записи ответа возьмем промежутки, в которых стоит знак «плюс», так как в условии стоит знак «>».
Ответ: (−5;1)∪(8;+∞).
Пример №2. Решить неравенство:
х(х – 6)≤0
В данном случае мы видим, что есть отличие от неравенства стандартного вида. Но помним, что в случае сложения или вычитания переменной х и нуля мы получим переменную х, т.е. неравенство могло выглядеть так:
(х±0)(х – 6)≤0
Значит, одним из нулей функции будет число нуль. Итак, имеем нули функции 0 и 6. Ставим их на числовом луче, помня о том, что точки будут «приколотые», расставляем знаки путем чередования справа налево:
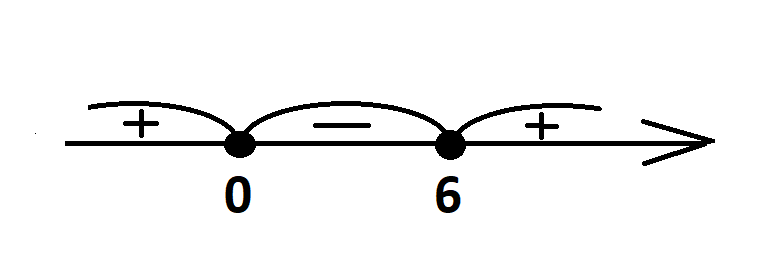 Записываем ответ в соответствии с условием (знак ≤), т.е. выбираем промежуток со знаком «минус».
Записываем ответ в соответствии с условием (знак ≤), т.е. выбираем промежуток со знаком «минус».
Ответ: [0; 6]
Пример №3. Решить неравенство:
(х+11)(4 – х)(x+2)<0
В данном случаем мы видим отличие от записи неравенства стандартного вида во втором произведении, т.е. в (4 – х). Поэтому для начала надо привести неравенство к стандартному виду, для этого вынесем за скобки минус единицу –1(х+11)(х – 4)(x+2)<0, а теперь разделим обе части неравенства на эту минус 1, поменяв знак неравенства на противоположный:
(х+11)(х – 4)(x+2)>0
Именно это неравенство будем решать. Итак, нули функции – это –11, 4 и –2. Расставляем их на числовом луче и расставляем знаки путем чередования, получим:
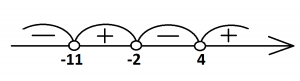
Ищем промежутки, соответствующие неравенству стандартного вида, к которому мы привели, т.е. для (х+11)(х – 4)(x+2)>0.
Ответ: (–11; –2)∪(4;+∞)