Равнобедренный и равносторонний треугольники | теория по математике 🎲 планиметрия

Равнобедренный треугольник

Определение

Равнобедренным называется треугольник, у которого две стороны равны. У данного треугольника АВС АВ=ВС. Равные стороны АВ и ВС называют – боковые, а сторону АС – основанием треугольника.

Свойства равнобедренного треугольника

  • У равнобедренного треугольника углы при основании равны. Так, у данного треугольника угол А равен углу В:
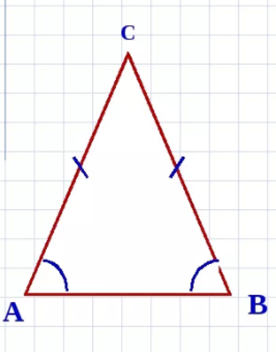
  • Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
  • Медиана равнобедренного треугольника, проведенная к основанию, является биссектрисой и высотой.
  • Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

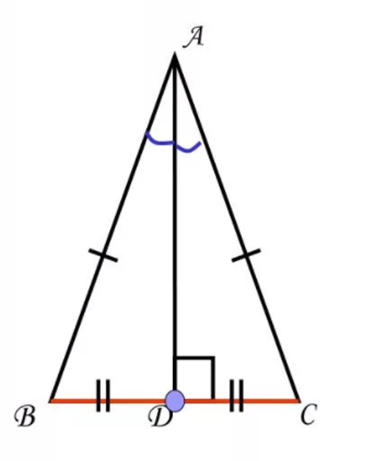
Свойства 2, 3 и 4 показаны на данном рисунке в треугольнике АВС. Мы видим, что отрезок АD, проведенный к основанию ВС, является биссектрисой (делит угол А пополам), медианой (ВD=DC), высотой (АD перпендикулярен ВС). Эти свойства работают для равнобедренного треугольника только тогда, когда отрезок проведен именно к основанию.

Равносторонний треугольник

Определение

Треугольник, у которого все стороны равны, называется равносторонним. На рисунке мы видим, что стороны АВ, ВС и АС равны.

Свойства равностороннего треугольника

  • У равностороннего треугольника все углы равны. Их величина – 60 градусов. В данном случае углы А, В и С равны, на рисунке они отмечены равным количеством дуг внутри каждого угла.
  • У равностороннего треугольника каждая биссектриса является медианой и высотой. И наоборот, каждая медиана является биссектрисой и высотой. Аналогично можно сказать и про высоту. Также, все эти отрезки равны между собой.

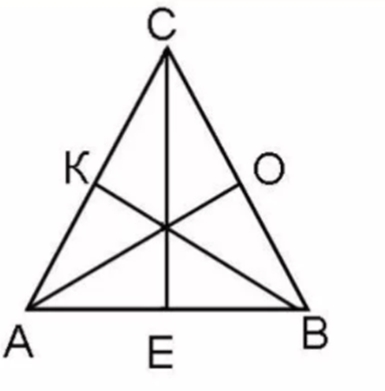
Так, если на рисунке показан равносторонний треугольник, то, например, каждая из медиан – АО, СЕ и КВ является высотой и биссектрисой.

Текст: Базанов Даниил, 13.7k 👀

Вся теория

Натуральные числа • Отношение чисел • Обратные числа • Обыкновенные дроби • Десятичные дроби • Перевод обыкновенной дроби в десятичную и наоборот • Бесконечные дроби и иррациональные числа • Округление чисел • Действия с рациональными числами • Действия со степенями • Числовые и буквенные выражения. Порядок действий. • Одночлен и его стандартный вид • Многочлены. Действия с многочленами. • Формулы сокращенного умножения. Разложение на множители. • Алгебраические дроби • Линейное уравнение • Неполные квадратные уравнения • Квадратное уравнение. Дискриминант. Теорема Виета. • Биквадратные уравнения • Числовые неравенства и их свойства • Линейные неравенства с одной переменной • Квадратные неравенства с одной переменной • Метод интервалов • Числовая последовательность • Арифметическая прогрессия и сумма ее членов • Геометрическая прогрессия и сумма ее членов • Функция. Зависимые и независимые переменные. Область определения и область значений функции. • Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства. • Линейная функция, ее свойства и график • Парабола, график, вершина, нули. • Гипербола. График функции и свойства. • Угол. Биссектриса. Виды углов. • Прямая. Параллельные и перпендикулярные прямые. • Плоскость. Прямая. Луч. Отрезок. Серединный перпендикуляр. • Треугольник. Медиана, биссектриса, высота, средняя линия. • Прямоугольный треугольник. Теорема Пифагора. • Признаки равенства треугольников • Неравенство треугольника • Окружность и круг • Вписанные и центральные углы, их свойства • Описанная и вписанная окружность • Четырехугольники • Умножение и его свойства • Шкала. Координатный луч. • Многоугольники. Равные фигуры. • Прямоугольный параллелепипед и его объем. Пирамида. • ВПР по Математике 8 класс • ВПР по математике 7 класс • ВПР по математике 6 класс • ВПР по математике 5 класс •