ВПР по математике 7 класс | теория по математике 🎲

Назначение КИМ для проведения проверочной работы по математике — оценить качество общеобразовательной подготовки по математике обучающихся 7 классов в соответствии с требованиями ФГОС. КИМ ВПР позволяют осуществить диагностику достижения предметных и метапредметных результатов обучения, в том числе овладения межпредметными понятиями и способности использования универсальных учебных действий (УУД) в учебной, познавательной и социальной практике. Содержание и структура проверочной работы определяются на основе Федерального государственного образовательного стандарта основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897) с учетом Примерной основной образовательной программы основного общего образования (одобрена решением Федерального учебно-методического объединения по общему образованию (протокол от 08.04.2015 № 1/15 (в редакции протокола № 1/20 от 04.02.2020)) и содержания учебников, включенных в Федеральный перечень.

Подходы к отбору содержания, разработке структуры проверочной работы: Всероссийские проверочные работы основаны на системнодеятельностном, компетентностном и уровневом подходах. В рамках ВПР наряду с предметными результатами обучения оцениваются также метапредметные результаты, в том числе уровень сформированности универсальных учебных познавательных, коммуникативных и регулятивных действий (УУД) и овладения межпредметными понятиями. Тексты заданий в вариантах ВПР в целом соответствуют формулировкам, принятым в учебниках, включенных в Федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.

Структура проверочной работы

Работа содержит 16 заданий. В заданиях 1–9, 11 и 13 необходимо записать только ответ. В задании 12 нужно отметить точки на числовой прямой. В задании 15 требуется схематично построить график функции. В заданиях 10, 14, 16 требуется записать решение и ответ.

Кодификаторы проверяемых элементов содержания и требований к уровню подготовки обучающихся

№ п/п	Проверяемые элементы содержания
1	Числа и вычисления
2	Алгебраические выражения
3	Уравнения
4	Функции
5	Координаты на прямой
6	Геометрия
7	Текстовые задачи
8	Статистика и теория вероятностей
9	Измерения и вычисления

Типы заданий

1. В заданиях 1, 2 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь» и вычислительными навыками.
2. В задании 3 проверяется умение извлекать информацию, представленную в таблицах или на графиках.
3. В задании 4 проверяется владение основными единицами измерения длины, площади, объёма, массы, времени, скорости.
4. Заданием 5 проверяется умение решать текстовые задачи на проценты.
5. Задание 6 направлено на проверку умений решать несложные логические задачи, а также находить пересечение, объединение, подмножество в простейших ситуациях.
6. В задании 7 проверяются умения извлекать информацию, представленную на диаграммах, а также выполнять оценки, прикидки.
7. В задании 8 проверяется владение понятиями «функция», «график функции», «способы задания функции».
8. В задании 9 проверяется умение решать линейные уравнения, а также системы линейных уравнений.
9. Задание 10 направлено на проверку умения извлекать из текста необходимую информацию, делать оценки, прикидки при практических расчётах.
10. В задании 11 проверяется умение выполнять преобразования буквенных выражений с использованием формул сокращённого умножения.
11. В задании 12 проверяется умение сравнивать обыкновенные дроби, десятичные дроби и смешанные числа.
12. Задания 13 и 14 проверяют умение оперировать свойствами геометрических фигур, применять геометрические факты для решения задач.
13. В задании 15 проверяется умение представлять данные в виде таблиц, диаграмм, графиков.
14. Задание 16 направлено на проверку умения решать текстовые задачи на производительность, покупки, движение.

Система оценивания

Правильное решение каждого из заданий 1–11, 13, 15 оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину; изобразил правильный рисунок. Выполнение каждого из заданий 12, 14, 16 оценивается от 0 до 2 баллов. Максимальный первичный балл — 19.

Перевод первичных баллов в отметки по пятибалльной шкале

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Первичные баллы	0–6	7–11	12–15	16-19

Задание №1

Найдите значение выражения: $\left(\frac{2}{5}+\frac{3}{4}\right):\frac{23}{20}$

В данном примере два действия. Выполним первое – в скобках, вспомним правило сложения обыкновенных дробей с разными знаменателями: надо найти общий знаменатель, для чисел 5 и 4 это будет 20, так как это наименьшее число, которое делится и на 5 и на 4 одновременно. Затем найти дополнительный множитель к дроби $\frac{2}{5}$ (надо 20:5, получим 4) и умножить его на числитель 2. Для второй дроби – надо 20 разделить на 4, получим 5, умножим 5 на числитель 3. Получим дроби $\frac{8}{20}+\frac{15}{20},$после этого надо сложить числители, а знаменатель оставить тот же. Распишем данное действие: $\frac{2}{5}+\frac{3}{4}=\frac{8}{20}+\frac{15}{20}=\frac{23}{20}$

Теперь выполняем деление. По правилу деления обыкновенных дробей надо делимое умножить на число обратное делителю, в данном случае числитель 23 сократится со знаменателем 23, а числитель 20 со знаменателем 20. Но самое простое, о чем надо помнить, что при делении двух одинаковых чисел, получается 1, запишем решение:

$\frac{23}{20}:\frac{23}{20}=\frac{23}{20}\bullet \frac{20}{23}=1$

Ответ: 1

Найдите значение выражения: $\frac{13}{6}:\frac{3}{2}-\frac{1}{9}$

В данном примере два действия. Выполним первое – деление. По правилу деления обыкновенных дробей надо делимое умножить на число обратное делителю. Запишем это так:

$\frac{13}{6}:\frac{3}{2}=\frac{13}{6}\bullet \frac{2}{3}$

Теперь выполним умножение обыкновенных дробей, предварительно сократив 2 и 6 на 2. Получим:

$\frac{13}{6}\bullet \frac{2}{3}=\frac{13}{3}\bullet \frac{1}{3}=\frac{13}{9}$

Теперь выполним второе действие – вычитание. Имеем дроби с одинаковыми знаменателями, поэтому вычитаем числители и полученную дробь сокращаем. Затем из неправильной дроби переведем в смешанную, разделив 4 на 3. Запишем решение:

$\frac{13}{9}-\frac{1}{9}=\frac{12}{9}=\frac{4}{3}=1\frac{1}{3}$

Ответ:$1\frac{1}{3}$

Задание №2

Найдите значение выражения (2,2 – 4,3):0,6.

В данном примере два действия. Выполним первое действие – в скобках. Из числа, модуль которого больше, это 4,3 вычтем число, которое по модулю меньше – это 2,2. Получаем отрицательное число (–2,1), так как 4,3 по модулю больше. Запишем это 2,2 – 4,3= –2,1. Теперь выполним следующее действие с полученным числом:

$\left(-2,1\right):0,6=-21:6=-3,5$

Перенеся запятые на одну цифру вправо в обоих множителях, так как у делителя после запятой одна цифра, получим деление целых чисел. Ответ будет отрицательным, так как выполняем деление двух чисел с разными знаками.

Ответ: $-3,5$

Найдите значение выражения: $\frac{2,8}{3,2-6,7}$

В данном задании мы видим дробное выражение, в знаменателе которого надо выполнить вычитание десятичных дробей, а затем выполнить деление числителя на знаменатель, так как помним, что дробная черта означает действие деление. Запишем решение:

$\frac{2,8}{3,2-6,7}=\frac{2,8}{-3,5}=-\frac{28}{35}=-\frac{4}{5}=-0,8$

При выполнении действия вычитания у нас получается отрицательное число в знаменателе, так как число 6,7 по модулю больше. При делении перенесли запятые вправо на одну цифру, так как в делителе одна цифра поле запятой, выполнили сначала сокращение дроби на 7, затем, поделив 4 на 5, получили десятичную дробь. Не забываем, что ответ отрицательный, так как делили два числа с разными знаками.

Ответ:$-0,8$

Задание №3

В таблице даны почтовые тарифы (в рублях) на стоимость пересылки письма в зависимости от его массы. Сколько рублей стоит пересылка заказного письма массой 58 г?

Вид письма	Стоимость пересылки (в рублях) письма массой
	0-19 г	20-39 г	40-59 г	60-79 г	80-99 г
Простое	22	26	29	32	35
Заказное	50	53	56	59	62
Ценное	110	113	116	119	122

Для ответа на вопрос задания надо найти в таблице необходимые данные, которые содержатся в вопросе, то есть пересылка заказного письмо массой 58 г. Находим в таблице эти данные (выделены синим цветом).

Вид письма	Стоимость пересылки (в рублях) письма массой
	0-19 г	20-39 г	40-59 г	60-79 г	80-99 г
Простое	22	26	29	32	35
Заказное	50	53	56	59	62
Ценное	110	113	116	119	122

Теперь на пересечении найденного столбца и строки определяем стоимость за пересылку (выделено синим цветом).

Вид письма	Стоимость пересылки (в рублях) письма массой
	0-19 г	20-39 г	40-59 г	60-79 г	80-99 г
Простое	22	26	29	32	35
Заказное	50	53	56	59	62
Ценное	110	113	116	119	122

Ответ: 56

В таблице показано, сколько дней в месяц выпадали осадки в Тюмени в течение некоторого года. Пользуясь данными, представленными в таблице, найдите, сколько дней в Тюмени выпадал снег в зимние месяцы.

Осадки	Месяц
	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
Дождь	0	0	2	9	16	17	17	19	19	4	4	0
Снег	14	19	15	8	4	0	0	0	2	5	8	10
Роса/иней	1	1	1	1	0	1	2	2	2	2	1	0

Для ответа на вопрос задания надо найти в таблице зимние месяцы (декабрь, январь, февраль) и строку с осадками «снег» (выделим это синим цветом)

Осадки	Месяц
	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
Дождь	0	0	2	9	16	17	17	19	19	4	4	0
Снег	14	19	15	8	4	0	0	0	2	5	8	10
Роса/иней	1	1	1	1	0	1	2	2	2	2	1	0

Теперь в строке «снег» и в выделенных столбцах находим количество осадков (выделим синим цветом)

Осадки	Месяц
	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
Дождь	0	0	2	9	16	17	17	19	19	4	4	0
Снег	14	19	15	8	4	0	0	0	2	5	8	10
Роса/иней	1	1	1	1	0	1	2	2	2	2	1	0

Теперь складываем найденные значения: 14+19+10=43

Ответ: 43

Задание №4

Автомобиль едет по дороге, проезжая 27 метров за каждую секунду. Выразите скорость автомобиля в километрах в час.

Для решения данной задачи надо вспомнить, сколько в 1 км метров и сколько в 1 часе секунд.

В 1 км=1000 м,$1час=60мин\bullet 60сек=3600сек$ (так как в 1 часе 60 минут, а в 1 минуте 60 секунд).

Для перевода 27 м/с надо данное число разделить на 1000 и умножить на 3600. Запишем это: $27:1000\bullet 3600=97,2км/ч$

Значит, скорость автомобиля 97,2 км/ч.

Ответ: 97,2 км/ч

Самолёт, находящийся в полёте, преодолевает 255 метров за каждую секунду. Выразите скорость самолёта в километрах в час.

Для решения данной задачи надо вспомнить, сколько в 1 км метров и сколько в 1 часе секунд.

В 1 км=1000 м,$1час=60мин\bullet 60сек=3600сек$ (так как в 1 часе 60 минут, а в 1 минуте 60 секунд).

Для перевода 255 м/с надо данное число разделить на 1000 и умножить на 3600. Запишем это: $255:1000\bullet 3600=918км/ч$

Значит, скорость самолета 918 км/ч.

Ответ: 918 км/ч

Задание №5

Кофеварку на распродаже уценили на 13%, при этом она стала стоить 6525 рублей. Сколько рублей стоила кофеварка до распродажи?

Задачу на проценты лучше оформить в виде таблицы или краткой записи, чтобы понять, что известно и что требуется узнать. Итак, в магазине продавалась кофеварка, какова её стоимость мы не знаем, но в процентном отношении это 100%. Затем её уценили на 13%, то есть она в процентном отношении стала стоить 100-13=87%, а это есть 6525 рублей.

Сделаем запись, обозначив неизвестное число за «х»:

Кофеварка	В рублях	В процентах
До распродажи	х	100
После распродажи	6525	87

Теперь видно, что решить можно с помощью пропорции, или как еще называют – «крестиком»: $х=\frac{6525\bullet 100}{87}=7500руб$

Таким образом, мы нашли ответ, что наша кофеварка до распродажи стоила 7500 рублей.

Ответ: 7500 рублей

Ежемесячная плата за телефон составляет 240 рублей. В следующем году она увеличится на 5%. Сколько рублей будет ежемесячная плата за телефон в следующем году?

Задачу на проценты лучше оформить в виде таблицы или краткой записи, чтобы понять, что известно и что требуется узнать. Итак, ежемесячная плата была 240 руб, в процентном отношении это 100%. Затем её увеличат на 5%, то есть она в процентном отношении станет 100+5=105%, а это сколько это будет, мы должны узнать.

Сделаем запись, обозначив неизвестное число за «х»:

Плата за телефон	В рублях	В процентах
Была	240	100
Стала	х	105

Теперь видно, что решить можно с помощью пропорции, или как еще называют – «крестиком»: $х=\frac{240\bullet 105}{100}=252руб$

Таким образом, мы нашли ответ, что абонентская плата станет 252 рубля

Ответ: 252 рубля

Задание №6

Лена младше Вероники на два года, но старше Оксаны на три года. Выберите верные утверждения и запишите в ответе их номера.

1. Любая девочка, помимо указанных, которая старше Оксаны, также старше Лены.
2. Среди указанных девочек нет никого младше Оксаны.
3. Вероника и Оксана одного возраста.
4. Любая девочка, которая старше Лены, также старше Оксаны.

Для логического решения данного задания можно изобразить данные на прямой, имея ввиду, что большие числовые значения располагаются справа на числовой прямой, а меньшие – слева. Обозначим кратко имена начальными буквами: Оксана – О, Лена – Л, Вероника – В. Расположим их согласно условию задачи: Лена младше Вероники, значит, она располагается левее Вероники; Лена старше Оксаны, значит, Оксана расположена левее Лены, так как она младше её.

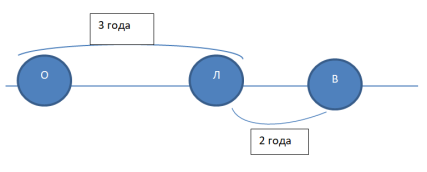
Теперь рассматриваем утверждения и определяем их истинность или ложность. Надо найти истинные, то есть верные суждения.

1. Любая девочка, помимо указанных, которая старше Оксаны, также старше Лены. Это ложное утверждение, так как любая девочка, кроме указанных, может быть и младше Лены.
2. Среди указанных девочек нет никого младше Оксаны. Это верное суждение, по схеме, которую мы составили это наглядно видно, что из указанных самая младшая – это Оксана.
3. Вероника и Оксана одного возраста. Это ложное суждение, что также видно по схеме.
4. Любая девочка, которая старше Лены, также старше Оксаны. Это верное суждение, так как по схеме видно, что самая младшая – Оксана, поэтому, все, кто старше Лены, будут и старше неё.

Можно было решать задачу другим способом, приняв за возраст Лены, например, 10 лет. Тогда Веронике будет 12 лет, а Оксане 7 лет. Затем рассуждать по каждому утверждению в соответствии с этими данными.

Итак, верные суждения под номерами 2 и 4. Запишем их в ответе.

Ответ: 24

Линейка стоит столько же, сколько карандаш и точилка вместе, а точилка дороже карандаша. Выберите верные утверждения и запишите в ответе их номера.

1. Две точилки стоят дешевле линейки.
2. Карандаш дороже точилки.
3. Линейка дороже точилки.
4. Линейка дороже карандаша.

Для решения данной задачи можно поработать с примерными ценами на данные приборы, придумав их сами.

Пусть, например, линейка стоит 50 рублей, тогда карандаш и точилка вместе стоят тоже 50 рублей, но сказано, что точилка дороже карандаша, например, точилка стоит 40 руб, а карандаш 10 руб.

Теперь рассматриваем утверждения и находим верные.

1. Две точилки стоят дешевле линейки. Если одна точилка стоит 40 руб, то две – 80 руб, а это дороже линейки, так как она стоит 50 руб. Значит, это неверное утверждение.
2. Карандаш дороже точилки. Это неверное утверждение, так как по условию сказано, что точилка дороже карандаша.
3. Линейка дороже точилки. Это верное утверждение, так как одна линейка стоит 50 руб, а это уже столько, сколько карандаш и точилка вместе.
4. Линейка дороже карандаша. Это верное утверждение, так же как и в пункте 3 (так как одна линейка стоит 50 руб, а это уже столько, сколько карандаш и точилка вместе).

Значит, верные утверждения получились под номерами 3 и 4.

Ответ: 34

Задание №7

На диаграмме показано содержание питательных веществ в ядрах миндаля. Определите по диаграмме, сколько примерно граммов углеводов содержится в 100 г ядер миндаля.

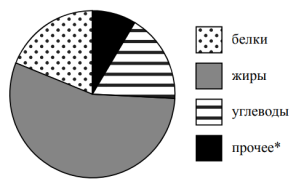
*К прочему относятся вода, витамины и минеральные вещества.

Определите по диаграмме, сколько примерно граммов углеводов содержится в 100 г ядер миндаля.

Пусть весь данный круг – это 100 г ядер миндаля. Тогда надо разделить круг на части, чтобы примерно найти содержание углеводов, которые обозначены горизонтальными линиями на белом фоне . Разделим сначала круг на 4 части, проведя, через его центр две прямые. Значит, 100:4=25 гр – это содержание углеводов и прочих веществ (покажем на рисунке). Теперь смотрим, сколько примерно составляют углеводы (обозначены буквой У) в этой части. Это примерно две трети от 25 граммов.

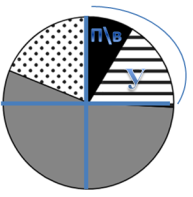
Чтобы найти эти две третьих от 25, надо $25\bullet \frac{2}{3}=\frac{50}{3}\approx 16,66..$ Округлим данное значение до целого, получим, приблизительно 17 граммов углеводов содержится в 100 граммах ядер миндаля.

Ответ: 17

На диаграмме показано содержание питательных веществ в ядрах абрикосовых косточек. Определите по диаграмме, сколько примерно граммов жиров содержится в 100 г ядер абрикосовых косточек.

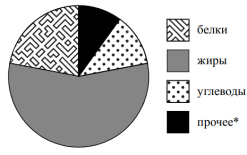
*К прочему относятся вода, витамины и минеральные вещества.

Пусть весь данный круг – это 100 г ядер абрикосовых косточек, а нам надо определить содержание жиров (показаны на диаграмме серым цветом). Проведем через центр круга прямую, разделив его на 2 равные части. Видно, что жиров больше половины круга, то есть более 50 граммов.

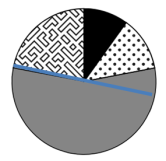
Теперь надо определить, на сколько больше половины содержится жиров. На диаграмме попробуем это показать, то есть сколько (примерно) раз небольшая частичка жиров войдет в нашу половину. Отметить можно штрихами, откладывая примерно одинаковые расстояния (можно использовать циркуль).

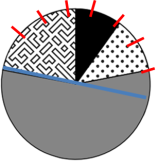
Видно, что примерно на 7 частей надо разделить половину, чтоб узнать остальное количество жиров. Итак, $50:7\approx 7,14\dots$ Округлим значение до целого числа, примерно 7 граммов, прибавим к найденным ранее 50 граммам и получим ответ – 57 граммов.

Ответ: 57

Задание №8

График функции $y=kx-1\frac{8}{11}$ проходит через точку $(9;3\frac{3}{11})$. Найдите коэффициент k.

Вспомним, как выглядит формула для графика линейной функции и что обозначает каждая буква в ней. Итак, формула:$y=kx+в$, где k – угловой коэффициент, х и у – переменные, а в – число на оси ординат (у), через которое проходит данная прямая. В нашем случае из формулы условия известно, что прямая проходит через точку $(0;-1\frac{8}{11})$ на оси ординат. Также по условию сказано, что прямая проходит через точку $(9;3\frac{3}{11})$, где х=9, а у=$3\frac{3}{11}$. Подставим данные значения переменных х и у в нашу формулу, получим:

$3\frac{3}{11}=k\bullet 9-1\frac{8}{11}$

Теперь надо решить полученное уравнение, перенеся известное в одну сторону, неизвестное в другую, не забывая при этом про знак при переносе. Получаем:

$3\frac{3}{11}+1\frac{8}{11}=9k$

Чтобы сложить два смешанных числа, складываем целые части и числители, так как знаменатели в данном случае одинаковые, получим: $4\frac{11}{11}=9k$

Преобразуем полученное смешанное число в целое:$5=9k$

Для нахождения переменной выполним деление:$k=5:9=\frac{5}{9}$

Итак, получили ответ $\frac{5}{9}$

Ответ:$\frac{5}{9}$

График функции $y=-\frac{7}{4}x+b$проходит через точку с координатами (6;-9) Найдите значение b.

Вспомним, как выглядит формула для графика линейной функции и что обозначает каждая буква в ней. Итак, формула:$y=kx+в$, где k – угловой коэффициент, х и у – переменные, а в – число на оси ординат (у), через которое проходит данная прямая. В нашем случае из формулы условия известно, что угловой коэффициент равен $-\frac{7}{4}$. Также по условию сказано, что прямая проходит через точку $(6;-9)$, где х=6, а у=$-9.$ Подставим данные значения переменных х и у в нашу формулу, получим:

$-9=-\frac{7}{4}\bullet 6+в$

Теперь надо решить полученное уравнение, умножив 6 на ($-\frac{7}{4}$) и перенеся известное в одну сторону, неизвестное в другую, не забывая при этом про знак при переносе. Получаем:

$-9+\frac{42}{4}=в$

Можно разделить 42 на 4, получим 10,5: $-9+10,5=в$

Выполним вычитание, получим:$1,5=в$

Итак, получили ответ 1,5

Ответ: 1,5

Конец решения

Задание №9

Решите уравнение $3\left(3х-4\right)+6-5х=14$

Вспомним алгоритм решения линейного уравнения: раскрытие скобок; перенос слагаемых (с переменной в одну часть, без переменной в другую), изменяя знаки при переносе; приведение подобных слагаемых; нахождение неизвестного.

Начинаем решение, следуя по алгоритму:

$3\left(3х-4\right)+6-5х=14$

Раскрываем скобки, умножая число 3 на каждое число в скобках, получим:$9х-12+6-5х=14$

Выполняем перенос слагаемых. В левой части остаются без изменения слагаемые с переменной, в правую часть к числу 14 переносим слагаемые 6 и минус 12, изменяя у них знаки на противоположные. Получим:$9х-5х=14+12-6$

Приводим подобные слагаемые:$4х=20$

Находим неизвестный множитель:$х=5$

Ответ: 5

Решите уравнение $-2х=13-3(2х-5)$

Вспомним алгоритм решения линейного уравнения: раскрытие скобок; перенос слагаемых (с переменной в одну часть, без переменной в другую), изменяя знаки при переносе; приведение подобных слагаемых; нахождение неизвестного.

Начинаем решение, следуя по алгоритму:

$-2х=13-3(2х-5)$

Раскрываем скобки, умножая число 3 на каждое число в скобках, получим:$-2х=13-6х+15$

Выполняем перенос слагаемых. В левой части остается без изменения слагаемое с переменной, к нему переносим минус 6х, изменяя знак; в правой части остаются числа 13 и 15. Получим:$-2х+6х=13+15$

Приводим подобные слагаемые:$4х=28$

Находим неизвестный множитель:$х=7$

Ответ: 7

Задание №10

Количество пряжи, необходимой для изготовления вязаного изделия, зависит от способа вязки, плотности вязки и качества нити. Моток лёгкой пряжи может содержать 600 м нити, а тяжёлой — до 200 м. Даже опытный мастер, начиная вязать свитер или большой шарф, может неверно оценить на глаз нужное количество пряжи. Часто поступают так: сначала мастер вяжет небольшой образец, рассчитывает его площадь и измеряет, сколько метров нити ушло на него. Таким образом, зная площадь будущего изделия, мастер может довольно точно оценить, сколько метров пряжи потребуется, чтобы связать изделие целиком.

Тамара Сергеевна собирается связать прямоугольную ажурную шаль длиной 150 см и шириной 80 см из тонкой пряжи. Ей нужно узнать, сколько потребуется пряжи. Для этого она связала пробный образец размером 10 см × 10см. На образец у неё ушло 15 м пряжи. В каждом мотке 650 м пряжи. Хватит ли Тамаре Сергеевне на шаль трёх мотков пряжи? Запишите решение и ответ.

В данном задании требуется подробно расписывать решение с пояснениями и рассуждениями.

В тексте сказано, что сначала мастер вяжет небольшой образец, рассчитывает его площадь и измеряет, сколько метров нити ушло на него. Таким образом, зная площадь будущего изделия, мастер может довольно точно оценить, сколько метров пряжи потребуется, чтобы связать изделие целиком. Значит, мы должны найти площадь образца, площадь будущего изделия, а только потом оценим, хватит ли пряжи.

Найдем площадь образца, зная, что его связали размером 10 на 10: $10\bullet 10=100{см}^2$

Найдем площадь готового изделия: $150\bullet 80=12000{см}^2$

Узнаем, сколько метров пряжи ей надо. Так как площадь шали 12000, а площадь образца 100, то разделив 12000 на 100 можно узнать, сколько таких образцов получится: 12000:100=120; теперь, зная, что на один образец ушло 15 метров, вычислим, сколько метров ей понадобится на всю шаль: $120\bullet 15=1800метров$

Зная, что в одном мотке 650 метров пряжи, а она планирует купить 3 мотка, прикинем, хватит ли ей пряжи: $650\bullet 3=1950м$. Так как 1950 больше, чем 1800, которые ей нужны, сделаем вывод, что трех мотков хватит.

Оформить решение с пояснением можно следующим образом:

$10\bullet 10=100{см}^2площадьобразца$

$150\bullet 80=12000{см}^2$ площадь готового изделия

12000:100*15=1800 метров ей понадобится на всю шаль

$650\bullet 3=1950м$ пряжи в планируемых трех мотках

$1950>1800$ трех мотков хватит

Ответ: хватит

Владимир работает в службе доставки интернет-магазина. Для упаковки коробок используется скотч. Он упаковал 200 маленьких коробок и израсходовал один рулон скотча полностью, а от второго осталось ровно две трети, при этом на каждую коробку расходовалось по 70 см скотча. Ему нужно заклеить скотчем 320 одинаковых коробок, на каждую нужно по 100 см скотча. Хватит ли трёх целых таких рулонов скотча?

В данном задании требуется подробно расписывать решение с пояснениями и рассуждениями.

Известно, что упаковано 200 коробок и израсходован 1 рулон целый и одна треть от второго (так как осталось две трети рулона), следовательно, израсходовали $1\frac{1}{3}$ рулона скотча на 200 коробок.

Далее сказано, что на каждую коробку он истратил по 70 см, значит, на 200 коробок он истратил $70\bullet 200=14000см=140м$ скотча. А это есть $1\frac{1}{3}$ рулона. Зная это, найдем, сколько метров в 1 рулоне: $140:1\frac{1}{3}=140\bullet \frac{3}{4}=35\bullet 3=105м$

Теперь рассмотрим, сколько ему надо обклеить коробок, по условию сказано 320 коробок по 100 см на каждую, то есть $100\bullet 320=32000см=320м$.

Хватит ли ему трех рулонов? Чтобы ответить на этот вопрос, умножим 105 на 3, получим 315 метров. Следовательно, трех рулонов не хватит.

Оформить решение с пояснением можно следующим образом:

$1+\frac{1}{3}=1\frac{1}{3}рулонаскотчаизрасходовали$

$70\bullet 200=14000см=140мскотчаизрасходовано$

$140:1\frac{1}{3}=140\bullet \frac{3}{4}=35\bullet 3=105мскотчав1рулоне$

$105\bullet 3=315мскотчавтрехрулонах$

$100\bullet 320=32000см=320мскотчапонадобится$

$315<320,значиттрехрулоновскотчанехватит$

Ответ: не хватит

Задание №11

Найдите значение выражения $-b\left(b+5\right)+({b+6)}^2приb=-\frac{2}{7}$

Данное выражение для начала нужно упростить, то есть раскрыть скобки, привести подобные слагаемые, а затем подставить значение переменной и вычислить.

Начинаем раскрывать скобки, умножая сначала число $-b$на каждое слагаемое в скобках, изменяя при этом знаки; вторая скобка раскрывается при помощи формулы сокращенного умножения – квадрат суммы двух выражений $({а+в)}^2={а}^2+2ав+{в}^2:$ $-b\left(b+5\right)+({b+6)}^2=-b^2-5b+b^2+12b+36$

Теперь приведем подобные слагаемые, увидев, что два противоположных, но равных по модулю слагаемых у нас взаимоуничтожаются, то есть в сумме дают нуль. Останется вычесть $-5b+12b$, получаем, что $-b^2-5b+b^2+12b+36=36+7b$

Теперь в данное выражение подставляем$b=-\frac{2}{7}$, получаем:

$36+7b=36+7\bullet \left(-\frac{2}{7}\right)=36-2=34$

При выполнении умножения у нас сократились семерки. Итак, полученное значение выражения равно 34.

Общая запись решения: $-b\left(b+5\right)+({b+6)}^2=-b^2-5b+b^2+12b+36=36+7b=36+7\bullet (-\frac{2}{7})=36-2=34$

Ответ: 34

Найдите значение выражения $\left(d+8\right)\left(-d-8\right)+8(2d+1)приd=6$

Данное выражение для начала нужно упростить, то есть раскрыть скобки, привести подобные слагаемые, а затем подставить значение переменной и вычислить.

Чтобы увидеть в начале выражения формулу, надо из второй скобки вынести минус; вторую скобку раскроем, умножая 8 на каждое слагаемое. Получаем:

$\left(d+8\right)\left(-d-8\right)+8\left(2d+1\right)=-\left(d+8\right)\left(d+8\right)+16d+8$

Теперь видим, что у нас получилось два одинаковых множителя, запишем выражение короче:

${-(d+8)}^2+16d+8$

Первая скобка раскрывается при помощи формулы сокращенного умножения – квадрат суммы двух выражений $({а+в)}^2={а}^2+2ав+{в}^2$

${-(d+8)}^2+16d+8=-d^2-16d-64+16d+8$

Приведем подобные слагаемые, увидев, что два из них взаимоуничтожаются, так как равны по модулю, но разные по знаку:

$-d^2-16d-64+16d+8=-d^2-56$

Подставляем теперь в наше выражение числовое значение, получаем:

$-d^2-56=-6^2-56=-36-56=-92$

Общая запись решения:

$\left(d+8\right)\left(-d-8\right)+8\left(2d+1\right)=-\left(d+8\right)\left(d+8\right)+16d+8=-{\left(d+8\right)}^2+16d+8={-d}^2-16d-64+16d+8=-d^2-56=-6^2-56=-36-56=-92$

Ответ: $-92$

Задание №12

Отметьте и обозначьте на координатной прямой точки $А\left(3\frac{5}{13}\right);В\left(-0,29\right);С(3,24)$

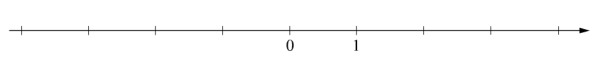
По условию мы видим, что одна из точек имеет отрицательную координату, значит, будет располагаться слева от нуля, ближе к нему, так как меньше половины единичного отрезка. Две другие точки в своих координатах содержат одинаковую целую часть, дробные же части – разного вида, что усложняет решение. Чтобы определить, какая из них будет ближе к тройке, разделим 5 на 13 приблизительно, получим примерно 0,38, следовательно, точка А будет иметь координату 3,38 и располагаться правее точки С, но не выходить за середину единичного отрезка, так как меньше 3,5. Теперь покажем эти точки на координатной прямой:

Отметьте и обозначьте на координатной прямой точки $А\left(2\frac{4}{15}\right);В\left(2,41\right);С(-1\frac{13}{18})$

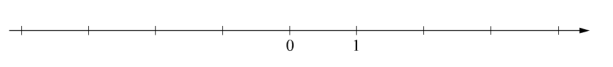
По условию мы видим, что одна из точек имеет отрицательную координату, значит, будет располагаться слева от нуля, остается выяснить ближе к единице или дальше от неё, так как дробная часть координаты точки С записана в виде обыкновенной дроби. Разделим 13 на 18, получим приблизительно 0,72, это больше половины единичного отрезка. То есть точка С имеет координату приблизительно (-1,72) и будет располагаться ближе к минус 2.

Две другие точки в своих координатах содержат одинаковую целую часть, дробные же части – разного вида, что усложняет решение. Чтобы определить, какая из них будет ближе к двойке, разделим 4 на 15 приблизительно, получим примерно 0,27, следовательно, точка А будет иметь координату 2,27 и располагаться левее точки В, но точка В не должна выходить за середину единичного отрезка, так как меньше 2,5. Теперь покажем эти точки на координатной прямой:

Задание №13

На клетчатой бумаге с размером клетки 1× 1 отмечены точки А, В и С. Найдите расстояние от точки A до прямой ВС.

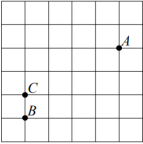
Чтобы найти расстояние до прямой ВС, ее надо провести на нашем рисунке. Затем сосчитать количество клеток от точки А прямо до прямой ВС, так как расстояние – это есть перпендикуляр, опущенный на данную прямую. Покажем это:

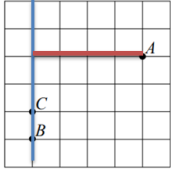
Синим цветом провели прямую ВС, красным – показали расстояние от точки А до этой прямой. Сосчитаем количество клеточек от А до ВС, получим 4. Значит, расстояние от точки A до прямой ВС равно 4.

Ответ: 4

На клетчатой бумаге с размером клетки 1 ×1 нарисованы два четырёхугольника: ABCD и ADEF. Найдите разность периметров четырёхугольников ABCD и ADEF.

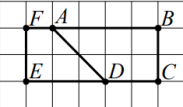
Вспомним, что периметр это сумма длин всех сторон. Так как надо найти разность периметров четырёхугольников ABCD и ADEF, то надо сначала составить периметры каждого из этих четырехугольников.

Периметр ABCD=AB+ВC+DC+AD, периметр ADEF=AD+DE+EF+FA. Подставим в каждый из них длины сторон, если их возможно найти по рисунку, считая клетки. Если невозможно найти длину стороны, оставим обозначение буквами.

ABCD=AB+ВC+DC+AD=4+2+2+ AD=8+ AD

ADEF=AD+3+2+1=6+ AD

Значит, разность между ABCD и ADEF равна 2,так как АD сторона и одного и второго четырехугольника. Или: ABCD– ADEF=8+ AD–(6+AD)=8-6=2

Ответ: 2

Задание №14

На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD=AC и точка A находится между точками B и D. Найдите величину угла ADC, если угол ABC равен 320

В данном задании требуется сделать чертеж, записать решение, обосновав его правилами.

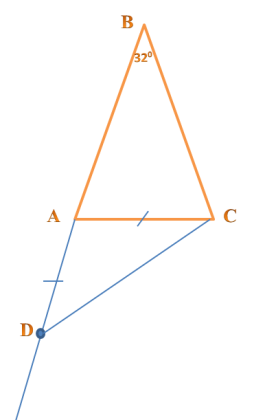Сначала выполним чертеж, следуя условию задачи: начертим равнобедренный треугольник АВС, обозначим так, чтобы основание было АС. Теперь продлим сторону ВА за точку А, отметим на продолжении точку Д так, чтобы АС=АД. Покажем это одинаковым количеством штрихов. Соединим Д и С, обозначим, что угол АВС равен 32 градуса. Приступаем к решению, которое надо записывать вместе с подтверждением. 1. Рассмотрим треугольник АВС – равнобедренный по условию, значит, угол ВАС равен углу ВСА как углы при основании. 2. Так как угол АВС=320, то угол ВАС=(1800-320):2=740 — сумма углов треугольника равна 1800 3. Рассмотрим треугольник АДС – равнобедренный по построению (АС=АД), значит углы АДС и АСД равны как углы при основании. 4. Найдем угол ДАС, 1800-740=1060 (углы ДАС и ВАС смежные по построению, значит, их сумма равна 1800). 5. Найдем угол АДС: (1800-1060):2 = 370 Ответ: 370

В данной задаче допускается другая последовательность действий, приводящих к верному ответу.

В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 7, а BC =14. Ответ дайте в градусах. Запишите решение и ответ

В данном задании требуется сделать чертеж, записать решение, обосновав его правилами.

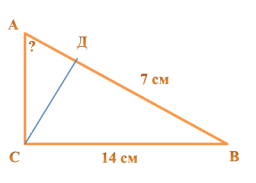Сначала выполним чертеж согласно условию задачи: построим прямоугольный треугольник АВС, где угол С=900, затем из прямого угла на гипотенузу АВ опустим перпендикуляр (высоту) ДС. Подпишем на сторонах данные – ВД=7 см, ВС=14 см. Теперь запишем решение задачи: Рассмотрим треугольник ВСД, где угол Д равен 900 по построению, значит треугольник ВСД прямоугольный, его гипотенуза ВС=14 см, а катет ВД=7 см. Следовательно, гипотенуза в два раза больше катета, а это значит, что угол ДСВ=300, так как катет, лежащий напростив угла в 300, равен половине гипотенузы. Значит, угол В равен 600 (сумма острых углов прямоугольного треугольника равна 900). Следовательно, по этому же правилу угол А будет равен 300 Ответ: 300

В данной задаче допускается другая последовательность действий, приводящих к верному ответу.

Задание №15

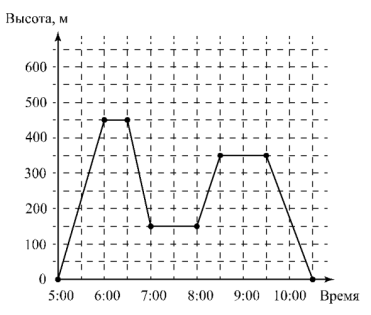
Воздушный шар — это летательный аппарат, который поднимается вверх за счёт нагревания воздуха, находящегося внутри шара. Высоту подъёма регулируют с помощью газовой горелки, которая нагревает воздух в шаре. Воздушный шар начал подъём с земли ровно в 5:00. За час он достиг высоты 450 метров. На протяжении следующего получаса горение газа поддерживали таким образом, что шар оставался на постоянной высоте. Затем пламя убавили, и летательный аппарат стал снижаться. Через полчаса была достигнута высота 150 метров, на которой шар оставался в течение часа, и была возможность любоваться красивыми видами. Затем пламя горелки увеличили, и за следующие полчаса шар поднялся до высоты 350 метров, на которой он оставался до 9:30. Потом в течение 60 минут шар плавно опускался на землю. Полёт завершился.

По описанию постройте схематично график зависимости высоты подъёма от времени суток. Соседние точки соедините отрезками. Точка, показывающая высоту подъёма в 5:00, уже отмечена на рисунке.

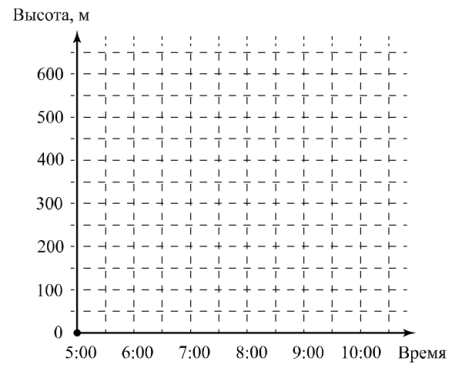
Чтобы понять, как выполнить построение, необходимо в тексте выделить главное (подчеркнуть, например) и на основании этого находить нужные точки.

Воздушный шар — это летательный аппарат, который поднимается вверх за счёт нагревания воздуха, находящегося внутри шара. Высоту подъёма регулируют с помощью газовой горелки, которая нагревает воздух в шаре. Воздушный шар начал подъём с земли ровно в 5:00. За час он достиг высоты 450 метров. На протяжении следующего получаса горение газа поддерживали таким образом, что шар оставался на постоянной высоте. Затем пламя убавили, и летательный аппарат стал снижаться. Через полчаса была достигнута высота 150 метров, на которой шар оставался в течение часа, и была возможность любоваться красивыми видами. Затем пламя горелки увеличили, и за следующие полчаса шар поднялся до высоты 350 метров, на которой он оставался до 9:30. Потом в течение 60 минут шар плавно опускался на землю. Полёт завершился.

Теперь работаем по подчеркнутым предложениям: начал подъём с земли ровно в 5:00. За час он достиг высоты 450 метров. Значит первая точка на нуле (подъем с земли), а вторая через час, то есть в 6:00 по времени на высоте 450 метров.

На протяжении следующего получаса горение газа поддерживали таким образом, что шар оставался на постоянной высоте. Значит, следующая точка на этой же высоте в 6:30.

Через полчаса была достигнута высота 150 метров, на которой шар оставался в течение часа. Значит, в 7:00 он опустился на высоту 150 м (ставим точку) и был там до 8:00 (ставим точку).

За следующие полчаса шар поднялся до высоты 350 метров, на которой он оставался до 9:30, следовательно в 8:30 он дошел до высоты 350 м (ставим точку) и на 9:30 ставим точку на этой же высоте.

В течение 60 минут шар плавно опускался на землю, значит, с 9:30 до 10:30 он шел в точку с нулевой отметкой.

Вот такой должен получиться график (точки лучше соединить, но задание считается выполненным верно, если точки не будут соединены)

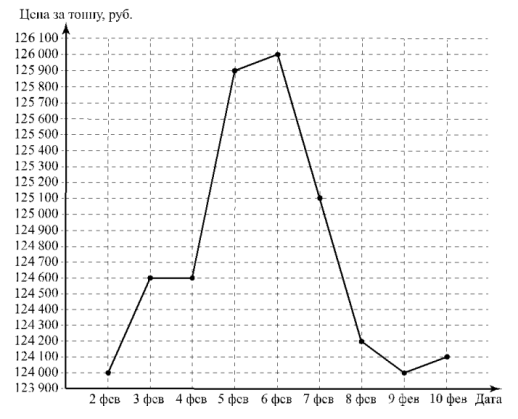
Цена на алюминий 2 февраля составляла 124 000 рублей за тонну. В выходные, 3 и 4 февраля, цена держалась на уровне 124 600 рублей за тонну. К открытию торгов в понедельник цена за тонну алюминия резко выросла на 1300 рублей, а на следующий день ещё на 100 рублей и достигла максимума за неделю. Следующие два дня цена снижалась на одинаковое количество рублей и 8 февраля составила 124 200 рублей. Цена продолжила снижаться и 9 февраля достигла того же значения, какое было 2 февраля, а 10 февраля цена на алюминий составила 124 100 рублей за тонну.

По описанию постройте график зависимости цены на алюминий (за тонну) от даты в течение девяти дней — со 2 февраля по 10 февраля. Соседние точки соедините отрезками. Точка, показывающая цену алюминия 2 февраля, уже отмечена на рисунке.

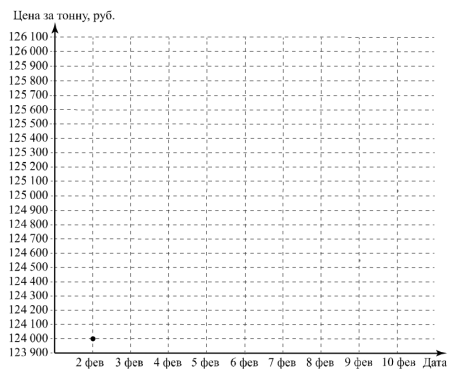
Знакомимся с текстом и выделяем для себя главное, намечаем решение.

Цена на алюминий 2 февраля составляла 124 000 рублей за тонну (эта точка есть на графике). В выходные, 3 и 4 февраля, цена держалась на уровне 124 600 рублей за тонну (значит, 3 и 4 февраля поставим точки напротив 124600). К открытию торгов в понедельник цена за тонну алюминия резко выросла на 1300 рублей (если 3 и 4 выходные, то понедельник 5 число и цена будет 124600+1300=125900, значит, ставим точку 5 числа напротив 125900), а на следующий день ещё на 100 рублей (это 6 число и прибавляем 100, то есть 126000) и достигла максимума за неделю. Следующие два дня цена снижалась на одинаковое количество рублей и 8 февраля составила 124 200 рублей (это 7 и 8 число; надо найти это одинаковое число, то есть от максимума 126000 отнять 124200 и разделить пополам, получим снижение на 900 руб, значит, 7 числа ставим точку на 126000-900=125100, 8 числа – надо 125100-900=124200). Цена продолжила снижаться и 9 февраля достигла того же значения, какое было 2 февраля (а 2 февраля у нас была точка на отметке 124000, значит ставим её на то же значение), а 10 февраля цена на алюминий составила 124 100 рублей за тонну (это уже дано готовое значение).

Итак, у нас должен получиться вот такой график. Точки можно соединять, можно не соединять.

Задание №16

В 9:00 велосипедист выехал из пункта А в пункт B. Доехав до пункта B, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и B.

Начинаем рассматривать задачу с того, что надо найти. Найти нужно расстояние между пунктами, для этого надо знать такие величины, как время и скорость. Скорость вообще не известна по условию, а только сказано, что она была постоянной туда и обратно. Разбираемся со временем: в 9:00 выехал из А в В, сделал остановку в В на 30 мин и поехал обратно в 11:30, значит, он прибыл в пункт В в 11:00. Тогда видно, раз выехал в 9:00, а прибыл в 11:00, следовательно, на весь путь затрачено 2 часа. Значит, в пункт А обратно он должен вернуться в 11:30+2 часа=13:30. По условию сказано, что в 13:00 ему осталось проехать 8 км, а по времени это 30 минут (0,5 часа). Зная это, мы можем найти скорость на данном участке пути: 8: 0,5=16 км/ч. Так как скорость была постоянной, то за 2 часа (путь от А до В) он проезжает $2\bullet 16=32км.$

Записать решение с пояснениями и рассуждениями в бланк можно следующим образом:

$11:30-9:00-30минут=2часа-времявпутиотАдоВ$

$11:30+2часа=13:30времяприбытиявпунктВ$

$13:30-13:00=30минут=0,5часаосталосьехать8кмпути$

$8:0,5=16\frac{км}{ч}скорость$

$16\bullet 2=32кмрасстояниеотАдоВ$

Ответ: 32 км

Может быть приведен другой способ решения, если он приводит к верному ответу

Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?

В данной задаче рассматривается движение двух объектов навстречу друг другу.

Рассмотрим, что известно про каждый автомобиль: скорость легкового неизвестна, скорость грузового на 15 км/ч меньше; До встречи каждый проехал 1 час, путь они проехали одинаковый – 135 км. Получается у нас недостаточно данных для решения, поэтому введем переменную «х». Пусть х – скорость легкового автомобиля, тогда (х-15) км/ч скорость грузового. Так как они ехали навстречу, то складываем их скорости, то есть $х+\left(х-15\right)=2х-15$это скорость сближения. Так как в пути они были 1 час, а расстояние 135 км, то (по формуле пути, где расстояние равно произведению времени и скорости) составим уравнение $1\bullet \left(2х-15\right)=135$

Решим данное уравнение:

разделим обе части на 1:$\left(2х-15\right)=135$

перенесем слагаемые, изменяя знак:$2х=135+15$

приведем подобные слагаемые в правой части:$2х=150$

найдем неизвестный множитель:$х=75$

Значит, скорость легкового автомобиля 75 км/ч, а скорость грузового 75-15=60 км/ч

Так как до встречи каждый из них проехал 1 час, то 135-60=75 км осталось проехать грузовику после встречи с легковым автомобилем

75:60=1,25 часа=75 мин через столько времени после встречи с легковым грузовик прибыл а пункт А

Ответ: через 75 минут

Допускается другая последовательность решения, приводящая к верному ответу.

Вся теория