Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
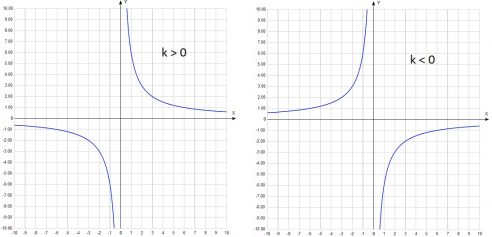
Свойства гиперболы (у=k/x)
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
- Область определения – любое число, кроме нуля.
- Область значения – любое число, кроме нуля.
- Функция не имеет наибольших или наименьших значений.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Построить график функции у=10x.
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное. 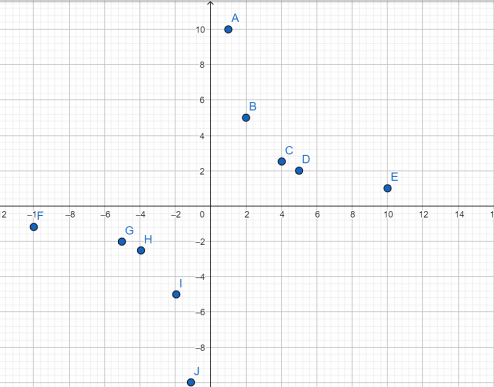
Теперь для построения гиперболы соединим точки плавной линией.
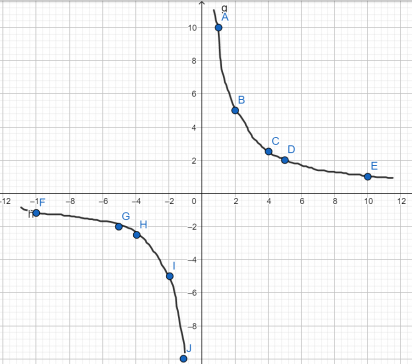
Построить график функции у=−5/x.
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
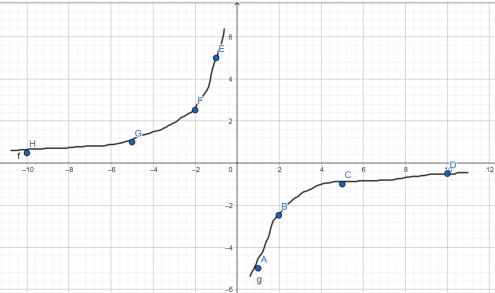
 1) y = x²
1) y = x²
Спасибо я поняла
у Вас в начале ошибка, общее уравнение гиперболы y=k/x, а у вас y=k*x
Сергей, спасибо большое, исправили!