Обозначения прямой
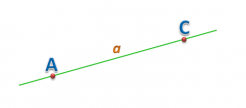
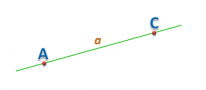
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.
Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.
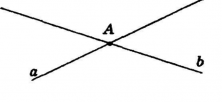
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а∩b=А, где ∩ — это знак «пересечение».
Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых
Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.
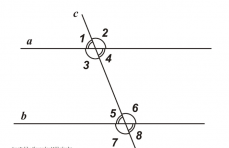
Необходимо запомнить названия следующих углов:
- накрест лежащие углы: 4 и 5; 3 и 6;
- односторонние углы: 4 и 6; 3 и 5;
- соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.
С данными углами связаны следующие признаки параллельности прямых:
- если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
- если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
- если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 1800, то прямые параллельны.
Аксиома параллельных прямых
Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.
Следствия из аксиом параллельных прямых
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.
- Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.
Перпендикулярные прямые
На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а⊥b, где «⊥» — знак перпендикулярности.
Заметим, что две прямые, перпендикулярные к третьей, не пересекаются.
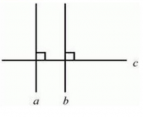
На данном рисунке а⟂с, b⟂c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.