Вписанные и центральные углы, их свойства • СПАДИЛО

Вписанный угол

Определение

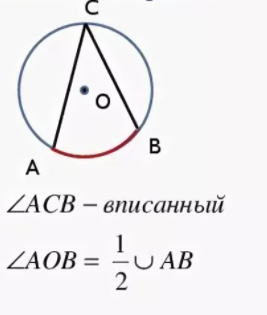
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Свойства вписанных углов

Свойство вписанного угла №1

Вписанный угол равен половине дуги, на которую он опирается.

На рисунке показан вписанный угол АСВ и дуга АВ, на которую он опирается. Если, например, дуга АВ=60⁰, то угол АСВ будет равен 30⁰. И наоборот, например, если угол АСВ равен 50⁰, то дуга АВ будет равна 100⁰.

Свойство вписанного угла №2

Вписанные углы, которые опираются на одну и ту же дугу, равны.

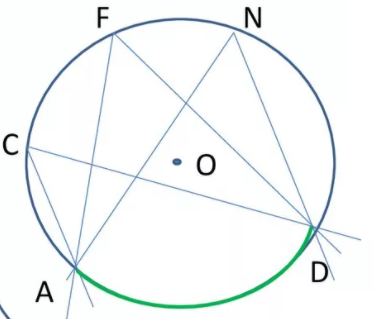
На рисунке показаны три вписанных угла – ACD, AFD, AND, которые опираются на одну и ту же дугу AD, поэтому эти углы равны.

Свойство вписанного угла №2

Вписанный угол, который опирается на диаметр, прямой.

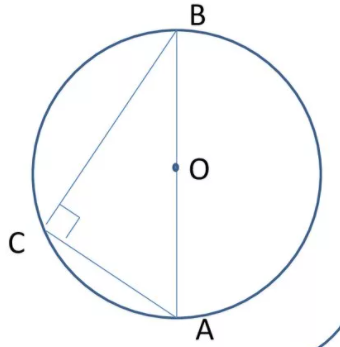
На рисунке угол ВСА опирается на диаметр АВ, следовательно, он равен 90⁰.

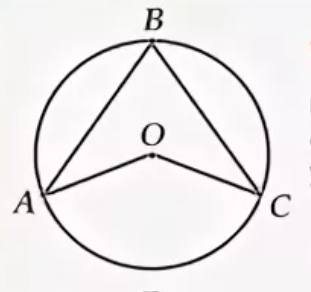
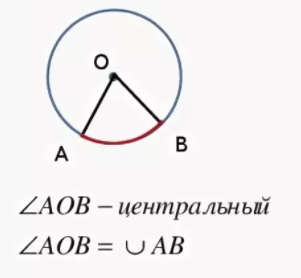
Центральный угол

Определение

Центральный угол – это угол, вершина которого лежит в центре окружности.

Свойства центральных углов

Свойство центрального угла

Центральный угол равен дуге, на которую он опирается.

На рисунке показан центральный угол АОВ, который опирается на дугу АВ. Например, дуга АВ равна 80⁰, тогда угол АОВ равен также 80⁰. И наоборот, например, если центральный угол АОВ будет равен 70⁰, то и дуга АВ также будет равна 70⁰.

Свойства вписанного и центрального угла

Если центральный и вписанный угол опираются на одну и ту же дугу, то вписанный угол равен половине центрального угла. И наоборот, центральный угол в 2 раза больше вписанного, если они опираются на одну и ту же дугу.

На рисунке показаны вписанный угол АВС и центральный угол АОС, которые опираются на одну и ту же дугу АС. Например, если величина угла АОС равна 120⁰, то величина угла АВС будет равна 60⁰.

Даниил Романович | Просмотров: 4.9k