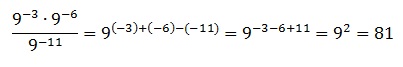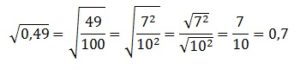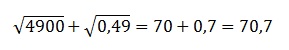Действия со степенями

$\frac{{(3\bullet 8)}^7}{3^7\bullet 8^5}$

В числителе дроби возведем в степень каждый множитель:

$\frac{{(3\bullet 8)}^7}{3^7}$=$\frac{3^7}{\bullet }$

Теперь сократим (выполним деление степеней), сократятся $3^7$ полностью, а при сокращении на $8^5$ по свойству степеней останется $8^2$, возведем 8 во вторую степень, получим 64, т.е.

$\frac{{(3\bullet 8)}^7}{3^7}$=$\frac{3^7}{\bullet }=8^2=64$

Найдите значение выражения:

при a = 13, b = 6,8

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

 Сокращаем (a-b):

 И получаем:

a/2

Подставляем значение a = 13:

13 / 2 = 6,5

Найдите значение выражения: (x + 5)² - x (x- 10) при x = - 1/20

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5)² — x (x — 10) = x² + 2 • 5 • x + 25 — x² + 10x

Затем приведем подобные слагаемые:

x² + 2 • 5 • x + 25 — x² + 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

Найдите значение выражения:

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:   По аналогии извлекаем и 2-й корень: В итоге получаем:

Значение какого из выражений является рациональным числом?

1. √6-3
2. √3•√5
3. (√5)²
4. (√6-3)²

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Какое из данных ниже чисел является значением выражения?

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

16 — 14 = 2

Суммарно наши действия выглядят так:

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ ?

1. 121ⁿ
2. 11ⁿ⁺²
3. 11²ⁿ
4. 11ⁿ⁺³

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

• при умножении степени складываются
• приделении степени вычитаются
• при возведении степени в степень степени перемножаются
• при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ = 11² • 11ⁿ

С учетом правила умножения, складываем степени:

  11² • 11ⁿ = 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

–0,3·(–10)⁴+4·(–10)²–59

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

–0,3·(–10)⁴+4·(–10)²–59 =

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

= –0,3·10000+4·100–59 =

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

= –3000+400–59 =

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

= –2600–59 =

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

= –(2600+59) = –2659