Многоугольники. Равные фигуры. | теория по математике 🎲 планиметрия

Определение

Многоугольник – это замкнутая ломаная, звенья которой не пересекаются. Рассмотрим это на рисунке 1. Так, первый многоугольник имеет четыре звена АВ, ВС, СД и АД. Этот многоугольник называется — четырехугольник. Каждое звено – это сторона, точки А,В, С и Д называются вершинами четырехугольника. Вершины бывают соседние и несоседние. Так, например, у многоугольника АВСД, соседними являются вершины А и В, В и С, С и Д, Д и А. Тогда несоседними являются вершины А и С, В и Д.

Многоугольник называют и обозначают по его вершинам последовательно, начиная с любой, т.е. имеем многоугольник АВСД. Можно назвать его ВСДА. Второй многоугольник – шестиугольник А1А2А3А4А5А6, т.е. он имеет 6 сторон, 6 вершин, 6 углов.

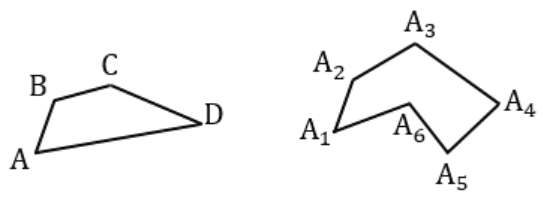
Рисунок 1

Фигура, изображенная на рисунке 2, не является многоугольником, так как её звенья АВ и СД пересекаются.

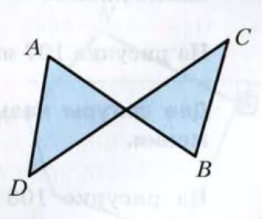
Рисунок 2

Обычно многоугольники называют по числу его углов, например, пятиугольник, восьмиугольник и т.д. Периметром многоугольника называют сумму длин всех его сторон.

Многоугольники называются равными, если они совпадают при наложении. Также и две фигуры называются равными, если они совпадают при наложении. Виды равных многоугольников и фигур приведены на рисунке 3.

Рисунок 3

Если соединить две несоседние вершины многоугольника, то получим отрезок, который называется диагональю многоугольника. Так, на рисунке 4 показаны диагонали АС и ВД.

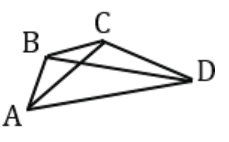
Рисунок 4

На рисунке 5 показаны все диагонали, проведенные из одной вершины А семиугольника ABCDEFK. Это диагонали AC, AD, AE, AF. Также можно провести еще по 4 диагонали из каждой другой вершины этого многоугольника.

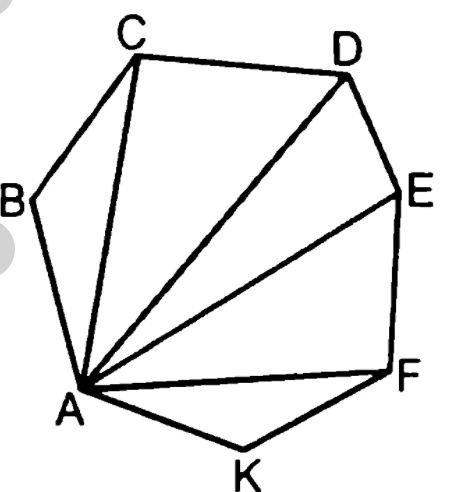
Рисунок 5

Текст: Базанов Даниил, 1k 👀

Вся теория

Натуральные числа • Отношение чисел • Обратные числа • Обыкновенные дроби • Десятичные дроби • Перевод обыкновенной дроби в десятичную и наоборот • Бесконечные дроби и иррациональные числа • Округление чисел • Действия с рациональными числами • Действия со степенями • Числовые и буквенные выражения. Порядок действий. • Одночлен и его стандартный вид • Многочлены. Действия с многочленами. • Формулы сокращенного умножения. Разложение на множители. • Алгебраические дроби • Линейное уравнение • Неполные квадратные уравнения • Квадратное уравнение. Дискриминант. Теорема Виета. • Биквадратные уравнения • Числовые неравенства и их свойства • Линейные неравенства с одной переменной • Квадратные неравенства с одной переменной • Метод интервалов • Числовая последовательность • Арифметическая прогрессия и сумма ее членов • Геометрическая прогрессия и сумма ее членов • Функция. Зависимые и независимые переменные. Область определения и область значений функции. • Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства. • Линейная функция, ее свойства и график • Парабола, график, вершина, нули. • Гипербола. График функции и свойства. • Угол. Биссектриса. Виды углов. • Прямая. Параллельные и перпендикулярные прямые. • Плоскость. Прямая. Луч. Отрезок. Серединный перпендикуляр. • Треугольник. Медиана, биссектриса, высота, средняя линия. • Равнобедренный и равносторонний треугольники • Прямоугольный треугольник. Теорема Пифагора. • Признаки равенства треугольников • Неравенство треугольника • Окружность и круг • Вписанные и центральные углы, их свойства • Описанная и вписанная окружность • Четырехугольники • Умножение и его свойства • Шкала. Координатный луч. • Прямоугольный параллелепипед и его объем. Пирамида. • ВПР по Математике 8 класс • ВПР по математике 7 класс • ВПР по математике 6 класс • ВПР по математике 5 класс •