Назначение КИМ для проведения проверочной работы по математике – оценить качество общеобразовательной подготовки обучающихся 5 классов в соответствии с требованиями ФГОС. ВПР позволяют осуществить диагностику достижения предметных и метапредметных результатов, в том числе уровня сформированности универсальных учебных действий (УУД) и овладения межпредметными понятиями.
Содержание проверочной работы соответствует Федеральному государственному образовательному стандарту основного общего образования (утвержден приказом Минобрнауки России от 17 декабря 2010 г. № 1897) с учетом Примерной основной образовательной программы основного общего образования (одобрена решением Федерального учебнометодического объединения по общему образованию (протокол от 08.04.2015 № 1/15 (в редакции протокола № 1/20 от 04.02.2020)) и содержания учебников, включенных в Федеральный перечень на 2021/22 учебный год.
Всероссийские проверочные работы основаны на системнодеятельностном, компетентностном и уровневом подходах. В рамках ВПР наряду с предметными результатами обучения учеников основной школы оцениваются также метапредметные результаты, в том числе уровень сформированности универсальных учебных действий (УУД) и овладения межпредметными понятиями. Предусмотрена оценка сформированности следующих УУД. Личностные действия: личностное, профессиональное, жизненное самоопределение. Регулятивные действия: планирование, контроль и коррекция, саморегуляция. Общеучебные универсальные учебные действия: поиск и выделение необходимой информации; структурирование знаний; осознанное и произвольное построение речевого высказывания в письменной форме; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; моделирование, преобразование модели. Логические универсальные действия: анализ объектов в целях выделения признаков; синтез, в том числе выведение следствий; установление причинно-следственных связей; построение логической цепи рассуждений; доказательство. Коммуникативные действия: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Структура проверочной работы
Работа содержит 10 заданий. В заданиях 1–4, 8, 9, 10 необходимо записать только ответ. В задании 10 (пункт 2) нужно изобразить требуемые элементы рисунка. В заданиях 5, 6,7 требуется записать решение и ответ.
Кодификатор проверяемых элементов содержания
| № п/п | Проверяемые элементы содержания |
| 1 | Числа и вычисления |
| 2 | Геометрические фигуры |
| 3 | Статистика и теория вероятностей |
| 4 | Измерения и вычисления |
| 5 | Текстовые задачи |
Типы заданий
- В заданиях 1–2 проверяется владение понятиями, «натуральное число», «обыкновенная дробь», «десятичная дробь».
- В задании 3 проверяется умение находить часть числа и число по его части.
- Заданием 4 контролируется умение находить неизвестный компонент арифметического действия.
- В заданиях 5, 7 проверяются умения решать текстовые задачи на движение, работу, проценты и задачи практического содержания.
- В задании 6 проверяется умение находить значение арифметического выражения с натуральными числами, содержащего скобки.
- В задании 8 проверяется умение извлекать информацию, представленную в таблицах, на диаграммах.
- Заданием 9 контролируется умение применять полученные знания для решения задач практического характера. Выполнение данного задания требует построения алгоритма решения и реализации построенного алгоритма.
- Задание 10 направлено на проверку умения применять геометрические представления при решении практических задач, а также на проверку навыков геометрических построений.
Система оценивания
Каждое верно выполненное задание 1–4, 9, 8 (пункт 1), 8 (пункт 2), 10 (пункт 1), 10 (пункт 2) оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину, изобразил правильный рисунок. Выполнение каждого заданий 5, 6, 7 оценивается от 0 до 2 баллов. Максимальный первичный балл за выполнение работы − 15.
Перевод первичных баллов в отметки по пятибалльной шкале
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичные баллы | 0–4 | 5–8 | 9–12 | 13-15 |
Задание №1
Найти значение выражения 378−58
Из условия следует, что нам надо выполнить вычитание обыкновенных дробей с одинаковыми знаменателями. Зная, что по правилу сложения (вычитания), знаменатель остается тот же, вычитаем только числители и получаем неправильную дробь 328. Теперь выполним деление числителя на знаменатель, зная, что дробная черта означает действие деление, и получим ответ 4.
Ответ: 4
Представьте число 8 в виде дроби со знаменателем 6.
Из условия следует, что нам необходимо получить обыкновенную дробь. Выполним для себя сначала запись, как указано в условии, чтобы 6 стояло в знаменателе, и подумаем, как найти числитель: 8=?6. Видим теперь, чтобы найти числитель, надо 6 умножить на 8, так как 8 это частное, а числитель — это делимое (так как дробная черта означает действие деление). По правилу нахождения делимого получим 48.
Ответ: 48
Задание №2
Запишите какое-нибудь число, расположенное между числами 42,93 и 42,94
Для нахождения числа необходимо помнить, как сравнивать десятичные дроби. Видим, что целые части у них равны, в обеих дробях по две цифры после запятой, значит нужно взять число, содержащее более двух цифр в десятичной части дроби, например 42, 931 или 42, 9325 и так далее, главное, чтобы целая часть и первые две цифры были равны 42,93, а последующие можно брать любые (одну или несколько). Помним, что, если берем только одну цифру, то она не должна равняться нулю, так как получится число, равное первому, что не удовлетворяет нашему заданию. В ответ нужно записать только одно число, например, 42, 9325.
Ответ: 42, 9325
Задание №3
В магазин завезли овощи. Пять девятых всех овощей — картофель, а две девятых всех овощей — помидоры. Сколько килограммов картофеля завезли в магазин, если помидоров завезли 72 кг?
По условию задачи можно составить краткую запись:
Картофель — 59 всех овощей;?кг
Помидоры — 29 всех овощей;72 кг
Из краткой записи видно, что помидоров было 72 кг, что составило 29 всех овощей. Значит, можно найти по числу и его части общее количество всех овощей. Для этого 72×9:2=324 (кг) всего овощей завезли. Зная, что картофеля было 59 от всего количества овощей, то есть от 324 кг, найдем, сколько килограммов его завезли. Для этого 324:9×5=180 (кг). Следовательно, в магазин завезли 180 кг картофеля.
Ответ: 180 кг
Осенью с яблонь сняли яблоки — жёлтые и зелёные. Зелёных яблок сняли 42 кг. Жёлтые яблоки составили пять двенадцатых всех яблок. Сколько всего килограммов яблок сняли?
Составим краткую запись:
Желтые яблоки — 512 всех яблок
Зеленые яблоки – 42 кг
Всего яблок — ? кг
Из краткой записи видно, что зеленых яблок было 42 кг, а какую часть всех яблок это составляет – неизвестно. Зная, что желтых яблок было 512, найдем, какую часть составляют зеленые. Для этого примем за одну целую общее количество яблок и вычтем из 1 число 512: 1−512=1212−512=712 составляют зеленые яблоки. Теперь найдем число по его части, то есть 42 кг – это 712 всех яблок. Значит, 42:7×12=72 (кг)было всего зеленых и желтых яблок.
Ответ: 72 кг
В гараже 30 зелёных машин, всего машин — 120. Какую часть составляют зелёные машины? Ответ выразите десятичной дробью.
Поскольку в гараже 120 машин, то 1 зеленая машина составляет 1120 всех машин, тогда 30 зеленых машин составляет 30120 всех машин. Так как ответ надо выразить десятичной дробью, то разделим числитель на знаменатель, получим 0,25.
Ответ: 0,25 составляют зеленые машины
На участке растут ели, берёзы и осины. Ели составляют две седьмых всех деревьев на участке, а берёзы — три седьмых. Сколько на участке осин, если берёз 21?
Составим краткую запись:
Ели – 27 всех деревьев;?штук
Березы — 37 всех деревьев;21 шт
Осины — ? шт
Из краткой записи видно, что берез было 21 и это составило 37 всех деревьев. Поэтому можно найти общее количество деревьев, как число по его части: 21:3×7=49 деревьев всего. Теперь найдем, сколько было елей (как часть от числа): 49:7×2=14 елей. Так как известно общее количество деревьев, количество елей и берез, то можно найти количество осин: 49-14-21=14 штук.
Ответ: 14 осин было на участке
Задание №4
Каким числом надо заменить букву, чтобы равенство стало верным?
572 — A =221 +157
В условии задания видим равенство, в котором можно найти сумму чисел 221 и 157, получим, что 572 — А=378. Отсюда видно, что число А является вычитаемым и находится вычитанием разности из уменьшаемого, то есть 572 – 378=194.
Ответ: 194
Какое число надо вписать в окошко, чтобы равенство стало верным?
819 : …. = 63
Из условия видно, что нам надо найти делитель по известным делимому и частному. По правилу его нахождения надо делимое 819 разделить на частное 63, получим 13.
Ответ: 13
Какое число надо вписать в окошко, чтобы равенство стало верным?
…. : 45 = 15
Из условия видно, что надо найти делимое по известным делителю 45 и частному 15. По правилу нахождения делимого умножаем 45 на 15, получим 675.
Ответ: 675
Какое число надо вписать в окошко, чтобы равенство стало верным?
…. · 24 = 432
Из условия видно, что нам надо найти неизвестный первый множитель по известному второму множителю и их произведению. По правилу нахождения множителя надо произведение 432 разделить на множитель 24, получаем 18.
Ответ: 18
Задание №5
За 7 часов 3D принтер напечатал 98 деталей. Сколько деталей напечатал этот 3D принтер за 6 часов? Запишите решение и ответ.
По условию задачи известно, что за 7 часов принтер печатает 98 деталей, следовательно, можно найти, сколько деталей печатает принтер за 1 час: 98:7=14 (деталей) за 1 час. Теперь легко найти, сколько деталей он напечатает за 6 часов, умножим 14 на 6, получаем 84 детали. Обязательно оформляем в бланке решение задачи со всеми пояснениями следующим образом:
- 98:7=14(д) печатает принтер за 1 час
- 14×6=84(д) печатает принтер за 6 часов
Ответ: 84 детали
За 7 дней ткацкий станок производит 3430 метров ткани. Сколько метров ткани произвёл этот станок за 4 дня? Запишите решение и ответ.
По известным данным (3430 метров ткани за 7 дней) можно найти количество метров ткани за 1 день, то есть 3430 разделим на 7, получим 490 метров. Теперь найдем, какое количество метров ткани произвёл станок за 4 дня, то есть 490 умножим на 4, получим 1960. Не забываем, что решение нужно оформить правильно:
- 3430:7=490(м)ткани за 1 день
- 490×4=1960(м) ткани за 4 дня
Ответ: 1960 метров
Самолёт летит со скоростью 9120 метров в минуту. Сколько метров он пролетел за 54 секунды? Запишите решение и ответ.
По условию задачи имеем разные величины – минуты и секунды. Вспомним, что в 1 минуте 60 секунд. Теперь, зная, что самолёт летит со скоростью 9120 метров в минуту, можем найти, сколько самолет пролетает за 1 секунду, разделим 9120 на 60, получаем, что 152 метра пролетает самолет за 1 секунду. Так как надо найти, сколько метров он пролетит за 54 секунды, то умножаем 152 на 54, получаем 8208 метров. Оформим решение задачи:
- 9120:60=152(м) пролетает за 1 секунду
- 152×54=8208(м) пролетает самолет за 54 секунды
Ответ: 8208 метров
От посёлка до города, расстояние между которыми 27 км, велосипедист проехал за полтора часа, а мотоциклист — на час быстрее. На сколько километров в час скорость мотоциклиста больше скорости велосипедиста? Запишите решение и ответ.
Для того, чтобы быстрее разобраться в условии задачи на движение, можно оформить данные в виде таблицы:
| Объекты движения | Скорость (км/ч) | Время (ч) | Расстояние (км) |
| Велосипедист | ? | 1,5 | 27 |
| Мотоциклист | ? | ?, на 1 час быстрее | 27 |
Теперь наглядно видно, что в столбце «время» не известно, сколько времени был в пути мотоциклист. Так как сказано, что он ехал на 1 быстрее (значит меньше), то 1,5-1=0,5 часа был в пути мотоциклист. Теперь работаем со столбцом «скорость». Вспоминаем, что для нахождения скорости надо расстояние разделить на время, следовательно, 27 делим на 1,5, получаем 18 км/ч скорость велосипедиста. Далее находим скорость мотоциклиста, который был в пути 0,5 часа, делим 27 на 0,5, получаем 54 км/ч. Смотрим, какой вопрос в нашей задаче. Мы должны узнать, на сколько километров в час скорость мотоциклиста больше скорости велосипедиста. Разницу в скоростях наших объектов движения находим вычитанием: 54-18=36 км/ч. Оформляем решение задачи правильно:
- 1,5-1=0,5 (ч) был в пути мотоциклист
- 27:1,5=18 (км/ч) скорость велосипедиста
- 27:0,5=54 (км/ч) скорость мотоциклиста
- 54-18=36 (км/ч) на столько скорость мотоциклиста больше скорости велосипедиста
Ответ: на 36 км/ч
Задание №6
Найдите значение выражения (14 − 12,725) · 12,4 − 2,6 : (11,2 − 7,95).
Первое и второе действия выполним в скобках:
- 14-12,725=1,275 (при вычитании в столбик надо приписать к числу 14 три нуля справа (14,000), так как в нем нет десятичной части; затем вычесть и поставить в ответе запятую под запятой)
- 11,2-7,95=3,25 (добавляем в уменьшаемом один нуль справа 11,20; вычитаем и ставим в ответе запятую под запятой). Третье и четвертое действия — это умножение и деление соответственно:
- 1,275∙12,4=15,81 (выполняем умножение, не обращая внимания на запятые; в ответе отделяем запятой столько цифр, сколько их в обоих множителях вместе после запятой, в нашем случае – 4 цифры; убираем нули в конце дроби)
- 2,6:3,25=260:325=0,8 (при делении на десятичную дробь надо перенести запятые вправо на столько цифр, сколько их после запятой в делителе; в нашем случае – на две; затем разделить полученные числа). Пятое последнее действие – вычитание. Вычитаем из результата третьего результат четвертого действия
- 15,81-0,8=15,01 (вычитаем по правилу вычитания десятичных дробей)
Не забываем записывать каждое действие в столбик в бланке.
Ответ: 15,01
Найдите значение выражения 162 + 20 · (5621 − 33) : 11.
В данном примере выполняются простые действия с натуральными числами.
Первое действие выполняется в скобках, затем идет умножение, потом деление, последнее – сложение.
- 5621 − 33 = 5588
- 20 · 5588 = 111 760
- 111 760 : 11 = 10 160
- 162 + 10 160 = 10 322
Не забываем, что в бланк надо записать каждое действие в столбик.
Ответ: 10322
Задание №7
В магазине продается несколько видов творога в различных упаковках и по различной цене. Какова наименьшая цена за килограмм творога среди данных в таблице видов? Запишите решение и ответ.
| Упаковка | Цена за упаковку |
| 200 г | 52 руб. |
| 250 г | 62 руб. |
| 300 г | 75 руб. |
| 200 г | 85 руб. |
Для решения задачи нам требуется узнать наименьшую цену за килограмм. В таблице приведены данные в граммах. Вспомним, что в 1 килограмме 1000 граммов. Для удобства и наглядности решения можно добавить в данной таблице третий столбик – цена за 1 кг и расписать в нем решение. Так как известно, что 1кг=1000 гр, то достаточно 1000 разделить на число указанных граммов (если числа делятся) и умножить на цену за упаковку. Последнюю строку можно не заполнять, так как видно, что упаковка 4 равна упаковке 1 по массе и она дороже.
| Упаковка | Цена за упаковку | Цена за 1 кг |
| 200 г | 52 руб. | 1000:200∙52=260 руб |
| 250 г | 62 руб. | 1000:250∙62=248 руб |
| 300 г | 75 руб. | Вычислим стоимость 1 грамма (так как 1000 не делится на 300): 75:300=0,25(руб).
Умножим 0,25 руб на 1000 гр, получим 250 руб |
| 200 г | 85 руб. | — |
Теперь выбираем самый дешевый творог, так как для ответа нужна наименьшая цена за килограмм творога. Это ответ из второй строки – 248 рублей.
Решение в бланке можно оформить как данной таблицей, так и выписать отдельно каждое действие.
Ответ: 248 рублей
Максим купил два ананаса, полкило сыра и два килограмма винограда. Один ананас стоит 24 рубля, один килограмм сыра — 480 рублей, а один килограмм винограда — 50 рублей. Какую сдачу получит Максим с 500 рублей? Запишите решение и ответ.
Для удобства можно оформить условие кратко, в виде таблицы.
| Вид покупки | Цена | Количество | Стоимость |
| Ананас | 24 руб за 1 шт | 2 шт | ? |
| Сыр | 480 руб за 1 кг | 0,5 кг | ? |
| Виноград | 50 руб за 1 кг | 2 кг | ? |
Теперь видим, что нам нужно найти стоимость каждого вида покупки. Можно записывать действия прямо в таблице. Вспомним, что для нахождения стоимости цену умножаем на количество.
| Вид покупки | Цена | Количество | Стоимость |
| Ананас | 24 руб за 1 шт | 2 шт | 24∙2=48 руб |
| Сыр | 480 руб за 1 кг | 0,5 кг | 480∙0,5=240 руб |
| Виноград | 50 руб за 1 кг | 2 кг | 50∙2=100 руб |
Теперь находим стоимость всей покупки: 48+240+100=388 руб
Зная, что Максим дал 500 руб, надо 500-388=112(руб) сдачи он получит
Ответ: 112 рублей
Биатлон — зимний вид спорта, сочетающий лыжную гонку со стрельбой из винтовки. В биатлоне за каждый промах при стрельбе по мишени биатлонисту ко времени прохождения дистанции добавляется 1 минута штрафного времени. В таблице показаны результаты четырёх биатлонистов. Каково наименьшее итоговое время с учётом штрафных минут? Запишите решение и ответ.
| Биатлонист | Время прохождения | Количество промахов |
| Иванов | 33 мин 28 сек | 1 |
| Петров | 34 мин 45 сек | 0 |
| Сидоров | 33 мин 12 сек | 2 |
| Сергеев | 34 мин 53 сек | 1 |
Зная, что за 1 промах добавляется штрафное время 1 минута, мы должны добавить (при наличии штрафов) соответствующее время в минутах.
Иванов: 1 промах, 33 мин 28 сек + 1 мин=34 мин 28 сек.
Петров: 0 промахов, время остается 34 мин 45 сек
Сидоров: 2 промаха, 33 мин 12 сек+2 мин=35 мин12 сек
Сергеев: 1 промах, 34 мин 53 сек + 1 мин=35 мин 53 сек
Теперь отвечаем на вопрос задачи – выбираем наименьшее время, это время у биатлониста Иванова, это 34 мин 28 сек.
Оформить решение задачи в поле бланка можно как по действиям, так и добавив справа в таблицу еще один столбец и вписав в него действия.
Ответ: 34 мин 28 сек
Нужно купить 60 кг стирального порошка. Данные о цене и массе стирального порошка в упаковке указаны в таблице. Сколько будет стоить самая дешёвая покупка? Ответ дайте в рублях.
| Стиральный порошок | Масса, кг | Цена, руб |
| «Миф» | 2 | 230 |
| «Ромашка» | 15 | 1400 |
| «Лотос» | 3 | 275 |
| «Аист» | 6 | 590 |
Решение данного вида задач можно расписывать по действиям или оформлять решение в виде таблицы.
Итак, нам надо узнать, сколько будет стоить самая дешевая покупка. Для этого надо узнать, а сколько же упаковок каждого порошка надо купить, чтоб было 60 кг. Для этого 60 кг будем делить на массу каждого порошка,
То есть:
60:2=30 упаковок — «Миф»
60:15=4 упаковки — «Ромашка»
60:3=20 упаковок – «Лотос»
60:6=10 упаковок – «Аист»
Теперь умножим каждое найденное число упаковок на их цену и выберем для ответа наименьшее:
230*30=6900 (руб) «Миф»
1400*4=5600 (руб) «Ромашка»
275*20=5500 (руб) «Лотос»
590*10=5900 (руб) «Аист»
Теперь видно, что самая дешевая покупка – это порошок «Лотос». Укажем в ответе полученный наименьший результат.
Ответ: 5500 рублей
Задание №8
Маша в течение недели читала книгу «Маугли». На диаграмме показано, сколько страниц она читала каждый день. По вертикали указано количество прочитанных страниц, по горизонтали — дни недели. Пользуясь этими данными, ответьте на вопросы.
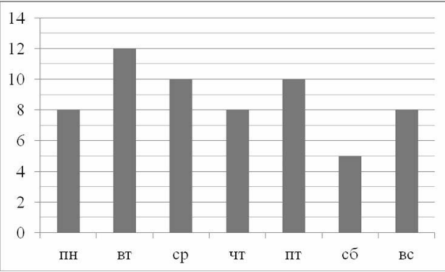
- Сколько страниц прочитала Маша во вторник?
- На сколько страниц меньше Маша прочитала в четверг, чем во вторник?
Чтобы ответить на первый вопрос, рассмотрим диаграмму. По условию сказано, что показано на вертикальной и на горизонтальной осях. Ищем на горизонтальной оси «вторник» (обведем красным цветом), двигаемся по этому столбцу вверх до его окончания и слева (на вертикальной оси) видим число 12 (показано стрелкой от столбца к числу). Это и есть наш ответ – 12страниц прочитала Маша во вторник.
Ответ: 12 страниц
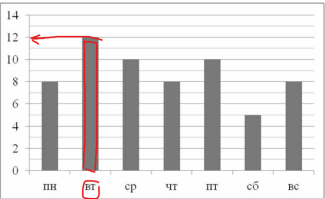
Рассмотрим, какие данные нужны, чтобы ответить на второй вопрос. Там речь идет о вторнике и четверге, а также о разнице в количестве прочитанных книг. Работаем с графиком. О количестве книг во вторник нам известно, их было 12. Также находим теперь на горизонтальной оси «четверг» (выделено зеленым цветом) и двигаемся вверх до окончания столбца, затем влево до указанного количества, видим, что их 8. Теперь находим, на сколько страниц меньше Маша прочитала в четверг, чем во вторник. Вспоминаем, что такая разница находится действием вычитания: 12-8=4 книги. Наш ответ 4.
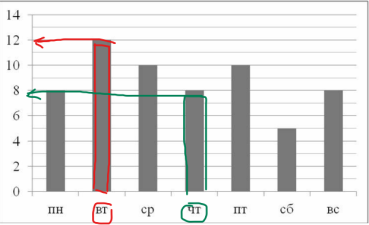
Ответ: на 4 книги
На диаграмме показана высота девяти самых высоких гор России. По вертикали указана высота в метрах над уровнем моря, по горизонтали — названия гор. Пользуясь этими данными, ответьте на вопросы.
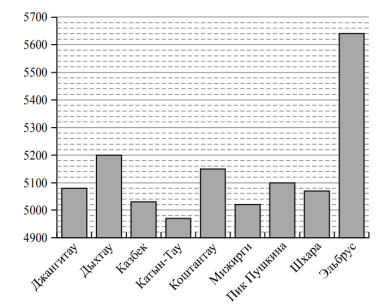
- Сколько на диаграмме гор высотой больше 5120 метров?
- Какая гора имеет высоту меньше 5000 метров?
На диаграмме рассмотрим, что указано по горизонтальной оси (названия гор), что указано на вертикальной оси (высота над уровнем моря). Чтобы ответить на первый вопрос, надо найти высоту 5120 метров на вертикальной оси. Там такого числа нет, следовательно, надо определить цену одного деления по этой оси (шкале). От 4900 до 5000 разница в 100 метров. А отрезков на шкале от 4900 до 5000 будет 5, значит 1 деление равно 100:5=20 метров.
Теперь находим на шкале число 5100 и поднимаемся на одно деление вверх, это и будет наша указанная высота – 5120 метров. Проведем от этого числа горизонтальную линию (показана красным цветом). 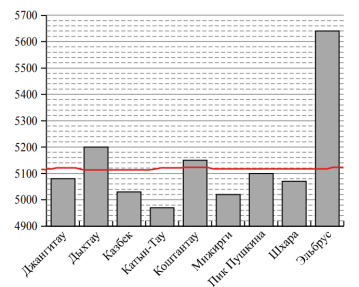
Теперь отвечаем на вопрос — сколько на диаграмме гор высотой больше 5120 метров. Считаем количество столбцов, которые выше этой линии (показаны синим цветом). Таких столбцов получилось три. Наш ответ 3.
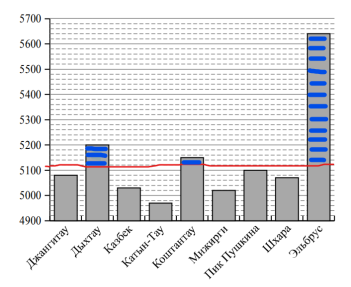
Ответ: 3 горы
Второй вопрос — какая гора имеет высоту меньше 5000 метров? Работаем с диаграммой. Находим высоту 5000 метров на вертикальной оси, проводим от этого числа горизонтальную линию (показана красным цветом).
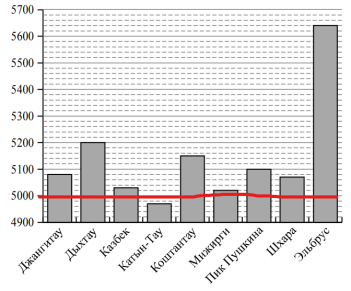
Теперь находим столбец, который ниже нашей линии, это столбец – гора Катын-Тау (показана синим цветом).
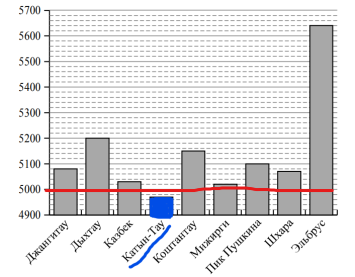
В ответе указывает название горы.
Ответ: Катын-Тау
На диаграмме показано, сколько золотых и серебряных медалей завоевали российские спортсмены на Олимпийских играх в разные годы.
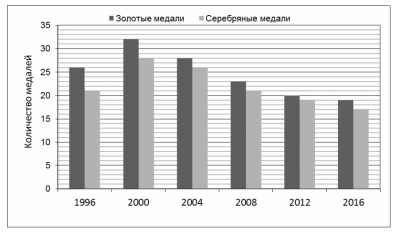
- В каком году количество полученных серебряных медалей наименьшее?
- Сколько всего золотых медалей завоевали российские спортсмены на Олимпийских играх 2000 и 2004 годов?
Для ответа на первый вопрос рассмотрим диаграмму, по горизонтальной оси указаны годы, по вертикальной – количество медалей. От каждого года вверх идут два столбца – черный и серый, черный – это золотые медали, серый – это серебряные. Будем работать с серым столбцом, чтобы найти в каком году количество серебряных медалей наименьшее. Ищем самый маленький серый столбец и соответствующий под ним год – 2016 (выделено красным цветом). Значит, в 2016 году было получено наименьшее количество серебряных медалей.
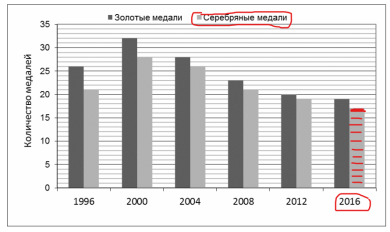
Ответ: в 2016 году
Для ответа на второй вопрос — сколько всего золотых медалей завоевали российские спортсмены на Олимпийских играх 2000 и 2004 годов, надо будет работать с золотыми медалями, они показаны на диаграмме столбцами черного цвета. Для определения количества медалей в каждом году надо знать цену деления, по вертикальной оси видно, что от 0 до 5 пять отрезков, значит, цена одного деления равна 1. Находим по горизонтальной оси 2000 и 2004 год и отмечаем их, от каждого черного столбца проведем линию влево до пересечения с вертикальной осью. Смотрим, сколько золотых медалей в 2000 году – получается 32, в 2004 году – 28. На рисунке это выделено синим цветом.
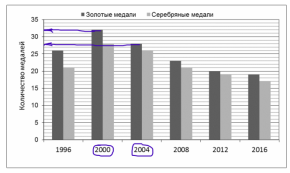
Теперь складываем их количество, так как надо найти, сколько всего медалей было: 32+28=60 медалей.
Ответ: 60 медалей
Задание №9
Найдите объём прямоугольного параллелепипеда по данным, указанным на рисунке. Ответ дайте в куб. см.
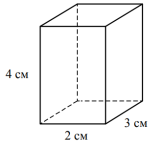
Вспомним, как находится объем прямоугольного параллелепипеда. Нужно знать формулу объема V=abc, где данные величины a, b, c – это соответственно длина, ширина и высота нашего прямоугольного параллелепипеда. Рассмотрим по рисунку, что длина равна 2 см, ширина 3 см, а высота 4 см. Перемножим данные величины: 2*3*4=24 см3 — объем данного параллелепипеда.
Ответ: 24 см3
Задание №10
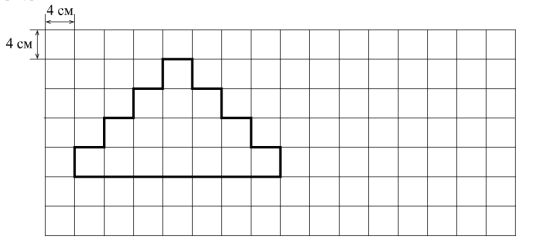
На рисунке дано поле, расчерченное на квадраты со стороной 4 см. На нём изображена фигура. Найдите периметр данной фигуры. Ответ дайте в сантиметрах. На поле, данном в условии, начертите прямоугольник, периметр которого равен 64 см.
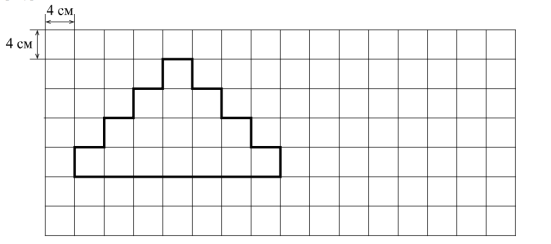
Для выполнения первой части этого задания необходимо просто сосчитать количество отрезков по клеточкам, то есть обойти фигуру от одной начальной точки. Рассмотрим это на рисунке, где синим цветом показана начальная точка. От неё «шагаем» по краю фигуры, чтобы попасть в эту же точку. Получим 22 отрезка по 4 см каждый, как указано в условии задания.
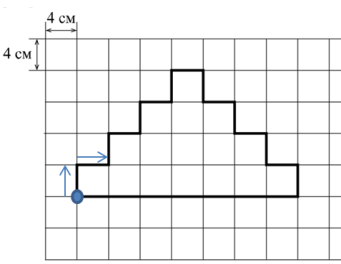
Теперь найдем периметр, умножив 4 на 22. Получаем 88 см. Это ответ на 1 часть задания.
Приступим ко второй части задания. На поле, данном в условии, надо начертить прямоугольник, периметр которого равен 64 см.
Имеем ввиду, что чертить мы будем в поле рядом с фигурой из первой части задания, так как нам нужно поле в клетку. Теперь вспомним, какие элементы надо знать для нахождения периметра прямоугольника – длину и ширину. Вспомним формулу периметра прямоугольника: P=(a + b)*2
Если наш периметр должен быть 64, то сумма одной длины и одной ширины должна равняться 32 (разделили периметр на два). Знаем, что длина стороны одной клетки равна 4, разделим 32 на 4 и получим 8. Значит, на нашу одну длину и одну ширину вместе приходится 8 отрезков. Например, длина 6, а ширина 2, длина 5, а ширина 3 и т.д. Выбираем удобный для нас вариант, чтобы фигура вошла в поле. Например, 5 и 3 и чертим прямоугольник с длиной 5 клеток, шириной 3 клетки.
Данный рисунок и будет являться решением второй части данного задания.