Треугольник. Медиана, биссектриса, высота, средняя линия. | теория по математике 🎲 планиметрия

Определение

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные Тупоугольные Прямоугольные
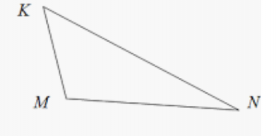
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. Прямоугольным называется треугольник, у которого есть угол, равный 900 (прямой угол). На рисунке угол С равен 900. Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний Равнобедренный Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Определение

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Определение

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Определение

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Определение

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Текст: Базанов Даниил, 13.6k 👀

Задание 25OM21R

В треугольнике АВС известны длины сторон АВ=36, АС=54, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

C:\Users\Учитель\Desktop\Inkedизображение_viber_2021-07-07_16-21-42-727_LI.jpg

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

AEAB..=ABAF.. откуда по свойству пропорции АВ2=АЕ∙АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

AEAD..=ACAF.. ; откуда выразим AD=AE∙AFАC..=AE∙AFAC..

Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC..

Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD=AE∙AFAC..=36254..=24

Теперь найдем CD=AC-AD=54-24=30

Ответ: 30

pазбирался: Базанов Даниил | обсудить разбор

Задание 18OM21R

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

Ответ: 4

pазбирался: Базанов Даниил | обсудить разбор

Задание 15OM21R

В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420

Ответ: 42

pазбирался: Базанов Даниил | обсудить разбор

Вся теория

Натуральные числа • Отношение чисел • Обратные числа • Обыкновенные дроби • Десятичные дроби • Перевод обыкновенной дроби в десятичную и наоборот • Бесконечные дроби и иррациональные числа • Округление чисел • Действия с рациональными числами • Действия со степенями • Числовые и буквенные выражения. Порядок действий. • Одночлен и его стандартный вид • Многочлены. Действия с многочленами. • Формулы сокращенного умножения. Разложение на множители. • Алгебраические дроби • Линейное уравнение • Неполные квадратные уравнения • Квадратное уравнение. Дискриминант. Теорема Виета. • Биквадратные уравнения • Числовые неравенства и их свойства • Линейные неравенства с одной переменной • Квадратные неравенства с одной переменной • Метод интервалов • Числовая последовательность • Арифметическая прогрессия и сумма ее членов • Геометрическая прогрессия и сумма ее членов • Функция. Зависимые и независимые переменные. Область определения и область значений функции. • Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства. • Линейная функция, ее свойства и график • Парабола, график, вершина, нули. • Гипербола. График функции и свойства. • Угол. Биссектриса. Виды углов. • Прямая. Параллельные и перпендикулярные прямые. • Плоскость. Прямая. Луч. Отрезок. Серединный перпендикуляр. • Равнобедренный и равносторонний треугольники • Прямоугольный треугольник. Теорема Пифагора. • Признаки равенства треугольников • Неравенство треугольника • Окружность и круг • Вписанные и центральные углы, их свойства • Описанная и вписанная окружность • Четырехугольники • Умножение и его свойства • Шкала. Координатный луч. • Многоугольники. Равные фигуры. • Прямоугольный параллелепипед и его объем. Пирамида. • ВПР по Математике 8 класс • ВПР по математике 7 класс • ВПР по математике 6 класс • ВПР по математике 5 класс •