Характеристика инструментария
Назначение КИМ для проведения проверочной работы по математике — оценить качество общеобразовательной подготовки обучающихся 8 классов в соответствии с требованиями ФГОС. КИМ ВПР позволяют осуществить диагностику достижения предметных и метапредметных результатов обучения, в том числе овладения межпредметными понятиями и способности использования универсальных учебных действий (УУД) в учебной, познавательной и социальной практике. Результаты ВПР в совокупности с имеющейся в общеобразовательной организации информацией, отражающей индивидуальные образовательные траектории обучающихся, могут быть использованы для оценки личностных результатов обучения.
Содержание и структура проверочной работы определяются на основе Федерального государственного образовательного стандарта основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897) с учетом Примерной основной образовательной программы основного общего образования (одобрена решением Федерального учебно-методического объединения по общему образованию (протокол от 08.04.2015 № 1/15 (в редакции протокола № 1/20 от 04.02.2020)) и содержания учебников, включенных в Федеральный перечень.
Всероссийские проверочные работы основаны на системнодеятельностном, компетентностном и уровневом подходах. В рамках ВПР наряду с предметными результатами обучения оцениваются также метапредметные результаты, в том числе уровень сформированности универсальных учебных познавательных, коммуникативных и регулятивных действий (УУД) и овладения межпредметными понятиями. Тексты заданий в вариантах ВПР в целом соответствуют формулировкам, принятым в учебниках, включенных в Федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.
Структура варианта проверочной работы
Работа содержит 19 заданий. В заданиях 1–3, 5, 7, 9–14 необходимо записать только ответ. В заданиях 4 и 8 нужно отметить точки на числовой прямой. В задании 6 требуется записать обоснованный ответ. В задании 16 требуется дать ответ в пункте 1 и схематично построить график в пункте 2. В заданиях 15, 17–19 требуется записать решение и ответ.
Кодификатор проверяемых элементов содержания
| № п/п | Проверяемые элементы содержания |
| 1 | Числа и вычисления |
| 2 | Алгебраические выражения |
| 3 | Уравнения |
| 4 | Функции |
| 5 | Координаты на прямой |
| 6 | Геометрия |
| 7 | Статистика и теория вероятностей |
Типы заданий
- В задании 1 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь», вычислительными навыками.
- В задании 2 проверяется умение решать линейные, квадратные уравнения, а также системы уравнений.
- В задании 3 проверяется умение решать задачи на части.
- В задании 4 проверяется знание свойств целых чисел и правил арифметических действий.
- Задание 5 проверяет владение понятиями «функция», «график функции», «способы задания функции».
- Задание 6 направлено на проверку умения извлекать и анализировать информацию, представленную в таблицах, на диаграммах, графиках.
- В задании 7 проверяются умения читать информацию, представленную в таблицах, на диаграммах, графиках и определять статистические характеристики данных.
- В задании 8 проверяется умение сравнивать действительные числа.
- В задании 9 проверяется умение выполнять преобразования буквенных дробно-рациональных выражений.
- Задание 10 направлено на проверку умения в простейших случаях оценивать вероятность события.
- Задание 11 проверяет умение решать текстовые задачи на проценты, в том числе задачи в несколько действий.
- Задания 12–15 и 17 проверяют умение оперировать свойствами геометрических фигур, а также знание геометрических фактов и умение применять их при решении практических задач.
- В задании 16 проверяются умения извлекать из текста необходимую информацию, представлять данные в виде диаграмм, графиков.
- Задание 18 направлено на проверку умения решать текстовые задачи на производительность, движение.
- Задание 19 является заданием высокого уровня сложности и направлено на проверку логического мышления, умения проводить математические рассуждения.
Система оценивания
Правильное решение каждого из заданий 1–5, 7, 9–14, 17 оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину; изобразил правильный рисунок. Выполнение каждого из заданий 6, 8, 15, 16, 18, 19 оценивается от 0 до 2 баллов. Максимальный первичный балл — 25.
Перевод первичных баллов
Перевод первичных баллов в отметки по пятибалльной шкале
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичные баллы | 0–7 | 8–14 | 15–20 | 21-25 |
Задание №1
Найдите значение выражения: 179:(29+14)
В данном примере два действия. Выполним первое – в скобках, вспомним правило сложения обыкновенных дробей с разными знаменателями: надо найти общий знаменатель, для чисел 9 и 4 это будет 36, так как это наименьшее число, которое делится и на 9 и на 4 одновременно. Затем найти дополнительный множитель к дроби 29 (надо 36:9, получим 4) и умножить его на числитель 2. Для второй дроби – надо 36 разделить на 4, получим 9, умножим 9 на числитель 1. Получим дроби 836+936, после этого надо сложить числители, а знаменатель оставить тот же. Распишем данное действие: 29+14=836+936=1736
Теперь выполняем деление. По правилу деления обыкновенных дробей надо делимое умножить на число обратное делителю, в данном случае числитель 17 сократится со знаменателем 17, а числитель 36 со знаменателем 9. Запишем решение:
179:1736=179∙3617=4
Ответ: 4
Найдите значение выражения −7,2:(1,16+1,24)
В данном примере два действия. Выполним первое действие – в скобках. Это сложение десятичных дробей, при котором надо запятую записать под запятой и выполнить сложение. Запишем это 1,16+1,24=2,4. Теперь выполним следующее действие — деление на полученное число:
(−7,2):2,4=−72:24=−3
Перенеся запятые на одну цифру вправо в обоих множителях, так как у делителя после запятой одна цифра, получим деление целых чисел. Ответ будет отрицательным, так как выполняем деление двух чисел с разными знаками.
Ответ: −3
Задание №2
Решите уравнение: 17х+2х2+21=0
Нам дано квадратное уравнение. Вспомним, что стандартный вид квадратного уравнения выглядит как ах2+вх+с=0, где а,в и с некоторые числа. Таким образом, наше уравнение надо привести к стандартному виду:
2х2+17х+21=0
Сначала надо найти дискриминант по формуле D=b2−4ac, выпишем для этого коэффициенты: a=2, b=17, c=21
Запишем: D=172−4∙2∙21=289−168=121>0 Значит, уравнение имеет два корня, которые находим по формуле:
−b±√D2a
x1=−17−√1212∙2=−17−114=−284=−7
x2=−17+√1212∙2=−17+114=−64=−1,5
Ответ: −7; −1,5
Задание №3
В спортивном зале находятся баскетбольные и футбольные мячи. Число баскетбольных мячей относится к числу футбольных как 4:7. Сколько всего мячей в спортивном зале, если баскетбольных мячей 28?
Примем за части данные из условия, то есть если число баскетбольных мячей относится к числу футбольных как 4: 7, то получается, что баскетбольные мячи составляют 4 части от общего количества мячей, а футбольные – 7. По условию баскетбольных 28 мячей, значит, можно найти, сколько мячей приходится на 1 часть: 28:4=7. Теперь найдем, сколько было футбольных мячей: 7∙7=49. Находим, сколько всего мячей было: 28+49=77
Ответ: 77 мячей
На кружок по математике записались семиклассники и восьмиклассники, всего 28 человек. Количество семиклассников, записавшихся на кружок, относится к количеству восьмиклассников как 4:3 соответственно. Сколько восьмиклассников записалось на кружок по математике?
Примем за части данные из условия, то есть если количество семиклассников, записавшихся на кружок, относится к количеству восьмиклассников как 4:3 соответственно, то получается, что семиклассники составляют 4 части от общего количества детей, а восьмиклассники – 3. Значит, всего частей было 7. По условию всего 28 детей, значит, можно найти, сколько детей приходится на 1 часть: 28:7=4. Теперь найдем, сколько человек приходится на 3 части, так как по условию задачи требуется найти количество восьмиклассников: 4∙3=12.
Ответ: 12 человек
Задание №4
На координатной прямой отмечены числа 0, a и b. Отметьте на этой прямой какое-нибудь число x так, чтобы при этом выполнялись три условия:х−а<0, х−b<0, −ахb<0

Решение
Для того, чтобы проще было выполнить задание, обозначим числами точки а и b. Например, а(1) и b(2,3)
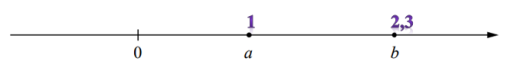
Для выполнения первого условия х−а<0 надо, чтобы х было меньше а, так как результат должен быть отрицательным. Значит, х должен располагаться левее а.
Для выполнения второго условия х−b<0 надо, чтобы х был тоже меньше b, так как результат должен быть отрицательным.
Таким образом, х должен быть и левее а, и левее b. Например, пусть х будет положительным числом 0,5.
Проверим третье условие с этим числом:
−ахb<0
Подставим наши числа в данное неравенство: −1∙0,52,3<0
При выполнении вычислений мы получим отрицательное число, следовательно, неравенство верное, значит, число х положительно и расположено между 0 и числом а. Покажем это на нашей координатной прямой, это и есть ответ к заданию:

На координатной прямой отмечены числа a, b и c. Отметьте на этой прямой какое-нибудь число x так, чтобы при этом выполнялись три условия:−a+x>0, b−x>0, x−c<0
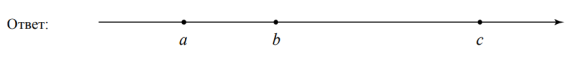
Решение
Для удобства нахождения решения примем а, b, c за 1, 2 и 4 соответственно:

Теперь проверим каждое из данных условий:
−a+x>0, подставим число: −1+x>0. Из неравенства видно, что х должен быть больше 1, чтобы результат стал положительным, то есть х должен располагаться правее а.
b−x>0, подставим число 2: 2−x>0. Из неравенства видно, что х должен быть меньше 2, так как результат должен быть положительным. Значит, х должен располагаться левее 2.
Так как из 1 и 2 условия следует, что х располагается между 1 и 2 (то есть между а и b), то и проверять условие 3 не имеет смысла. Выполним решение задания, покажем его на координатной прямой:

Задание №5
Прямая y =kx− 4 проходит через точку (3; −19). Найдите k.
Так как прямая проходит через данную точку, то надо подставить её координаты в формулу, выполним это, зная, что х=3; у=−19.
−19=3k−4
В полученном уравнении перенесем слагаемые с переменной в одну часть, а числа в другую, не забывая при этом изменить знаки:
−19+4=3k
Приведем подобные слагаемые в левой части:
−15=3k
Найдем значение k:
k=−5
Ответ: k=−5
Дана функция у=−53х+14. Найдите значение x, при котором значение функции равно −6.
Так как по условию известно, что значение функции равно −6, то можно подставить это значение в формулу. Выполним это:
−6=−53х+14
В полученном уравнении перенесем слагаемые с переменной в одну часть, а числа в другую, не забывая при этом изменить знаки:
−6−14=−53х
Приведем подобные слагаемые в левой части:
−20=−53х
Найдем значение х:
х=−20:(−53)=20∙35=12
Ответ: х=12
Задание №6
Пассажиропоток — это количество пассажиров, которых перевозит определённый вид транспорта за определённый промежуток времени (час, сутки, месяц, год). Пассажиропотоком называют также количество пассажиров, проходящих за определённый промежуток времени через транспортный узел (вокзал, аэропорт, автостанцию). Особенностью пассажиропотоков является их неравномерность и изменчивость: они зависят от времени, от направления и от других факторов. Изменение пассажиропотока в зависимости от месяца или времени года называется сезонностью пассажиропотока. На диаграмме показан пассажиропоток аэропорта им. Д.А. Хворостовского (Красноярск) в 2019 году. На сколько, примерно человек снизился пассажиропоток в сентябре по сравнению с августом? Чем можно объяснить рост пассажиропотока во второй половине лета? Напишите несколько предложений, в которых обоснуйте своё мнение по этому вопросу.
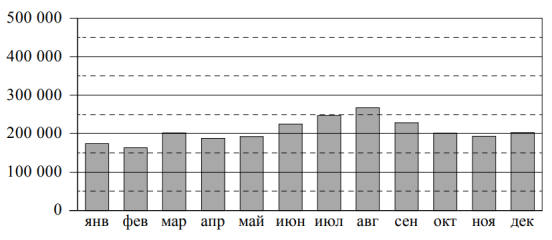
Рассмотрим пассажиропоток в сентябре и августе. Проведем от них горизонтальные линии на шкалу с количеством человек, подпишем на шкале, что одно деление это 50000 человек.
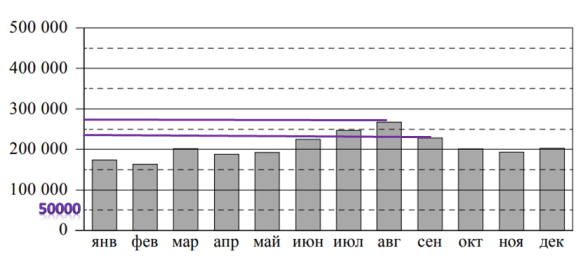
Найдем пассажиропоток в августе и сентябре, показав его количество на графике.
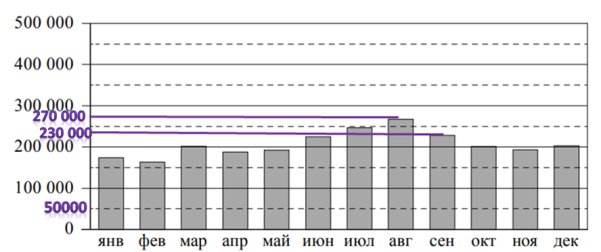
Примерное количество в августе 270000 человек, в сентябре — 230000 человек. Видно, что снизился пассажиропоток в сентябре по сравнению с августом на 40 000 человек. Это ответ на первый вопрос задания: 40000 человек.
Теперь необходимо написать рассуждения о том, чем можно объяснить рост пассажиропотока во второй половине лета?
Ответить можно так: Рост пассажиропотока во второй половине лета происходит потому, что многие берут отпуск и путешествуют. Также школьники и студенты находятся на каникулах.
Возможны построить предложения по-другому, но связать их желательно с отпусками и каникулами.
Загруженность автомобильных дорог измеряется в баллах по десятибалльной шкале. Для каждого значимого маршрута в городе определяется эталонное время, за которое его можно проехать по свободной дороге, не нарушая правил дорожного движения. Сравнивая время проезда по тем же улицам при текущей дорожной ситуации и эталонное время, компьютер вычисляет загруженность дороги в баллах. Загруженность автомобильных дорог в 1–2 балла означает, что дороги практически свободны, а если загруженность выше 7 баллов, то пользоваться автомобилем нецелесообразно. На графике показана средняя загруженность дорог в Москве в некоторый будний день. На графике видны два «всплеска» в течение суток. Чем их можно объяснить? Второй «всплеск» шире первого. Какими причинами это может быть вызвано? Напишите несколько предложений, в которых обоснуйте своё мнение по этим вопросам.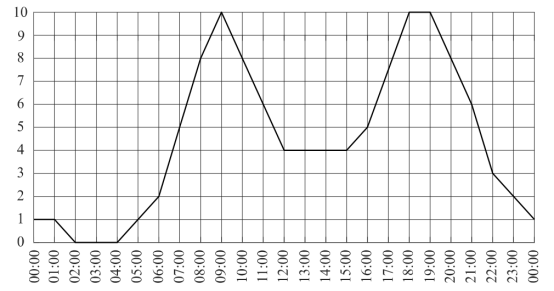
Для того, чтобы ответить на вопрос задания, необходимо рассмотреть диаграмму и понять, в какое время суток был «всплеск» на дорогах. Видно, что наивысший показатель в 10 баллов был в 9 утра и с 18.00 до 19.00 вечера.
Покажем эти места на графике:
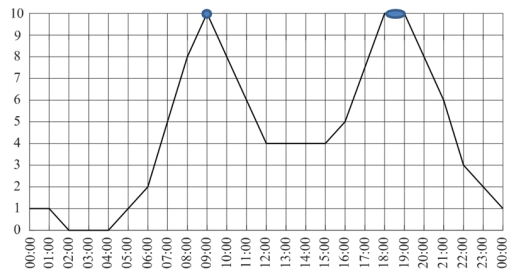
Также видно, что второй «всплеск» шире, то есть с 18.00 до 19.00.
Теперь обоснуем найденные данные, чтобы записать решение в бланк.
На графике показаны два «всплеска» — утром в 9.00 и вечером с 18.00 до 19.00, так как утром в это время большинство людей едет на работу или на учебу, а вечером они возвращаются. В вечернее время дороги более загружены, чем утром, так как люди еще заезжают в магазины, например, или по каким-то еще делам.
Возможны построить предложения по-другому, но они должны быть правдоподобными и логичными в изложении.
Задание №7
Коэффициент Бергера используется для распределения мест в шахматных турнирах среди нескольких участников, набравших равное количество очков. Коэффициент Бергера участника равен сумме всех очков противников, у которых он выиграл, плюс половина суммы очков противников, с которыми он сыграл вничью. Александр Гусев — один из участников шахматного турнира, состоящего из 8 туров. В таблице показано количество очков, набранных в турнире соперниками Александра, и результат игры с Александром. 1 — выиграл Александр, 0,5 — ничья, 0 — проиграл Александр. Вычислите коэффициент Бергера шахматиста Александра Гусева.
| Тур | Соперник | Очки | Результат |
| 1 | Денисов Егор | 5,0 | 0 |
| 2 | Васильев Павел | 3,0 | 1 |
| 3 | Чистяков Михаил | 4,0 | 1 |
| 4 | Волкова Светлана | 6,5 | 0,5 |
| 5 | Алексеев Даниил | 5,5 | 1 |
| 6 | Дружинина Мария | 3,0 | 0,5 |
| 7 | Антонов Ярослав | 7,0 | 0 |
| 8 | Осипов Егор | 5,5 | 0,5 |
Чтобы ответить на вопрос задания, надо знать алгоритм нахождения. Он указан в условии: коэффициент Бергера участника равен сумме всех очков противников, у которых он выиграл, плюс половина суммы очков противников, с которыми он сыграл вничью.
Итак, сначала найдем сумму всех очков противников, у которых он выиграл, то есть результат должен быть равен 1. Выделим это в таблице:
| Тур | Соперник | Очки | Результат |
| 1 | Денисов Егор | 5,0 | 0 |
| 2 | Васильев Павел | 3,0 | 1 |
| 3 | Чистяков Михаил | 4,0 | 1 |
| 4 | Волкова Светлана | 6,5 | 0,5 |
| 5 | Алексеев Даниил | 5,5 | 1 |
| 6 | Дружинина Мария | 3,0 | 0,5 |
| 7 | Антонов Ярослав | 7,0 | 0 |
| 8 | Осипов Егор | 5,5 | 0,5 |
Сумма очков: 3,0+4,0+5,5=12,5
Теперь нам надо найти и прибавить половину суммы очков противников, с которыми он сыграл вничью, это с результатом 0,5. Выделим их в таблице.
| Тур | Соперник | Очки | Результат |
| 1 | Денисов Егор | 5,0 | 0 |
| 2 | Васильев Павел | 3,0 | 1 |
| 3 | Чистяков Михаил | 4,0 | 1 |
| 4 | Волкова Светлана | 6,5 | 0,5 |
| 5 | Алексеев Даниил | 5,5 | 1 |
| 6 | Дружинина Мария | 3,0 | 0,5 |
| 7 | Антонов Ярослав | 7,0 | 0 |
| 8 | Осипов Егор | 5,5 | 0,5 |
Сумма очков: 6,5+3,0+5,5=15; половина суммы – это 15:2=7,5
Теперь складываем эти данные: 12,5+7,5=20
Итак, коэффициент Бергера шахматиста Александра Гусева равен 20
Ответ: 20
В таблице указаны тарифы на почтовые отправления в регионы России (по железной дороге). Посылки массой от 10 кг до 20 кг считаются тяжеловесными. Посылки, по сумме измерений превосходящие 120 см либо превосходящие хотя бы по одному измерению 60 см, считаются крупногабаритными. Максимальный разрешённый размер посылок по России 190×130×350 см. Если посылка тяжеловесная или крупногабаритная (негабаритная), она отправляется с наценкой 40%. Из Тулы в Воронеж отправили посылку массой 19 кг. Размеры посылки 49×28×39 см. Расстояние между городами по железной дороге 485 км. Дополнительные услуги не предусмотрены. Сколько рублей стоит отправление такой посылки?
| Расстояние | Менее 600 км | 600–2000 км | 2000–5000 км | 5000–8000 км | Более 8000 км |
| Тариф за массу до 500 г (руб.) | 194 | 263 | 274 | 329 | 270 |
| Дополнительно за каждые полные / неполные 500 г (руб.) | 22 | 25 | 34 | 49 | 56 |
Для ответа на вопрос задания надо определить тип нашей посылки. По условию — посылки массой от 10 кг до 20 кг считаются тяжеловесными, наша весит 19 кг, значит она тяжеловесная. Посылки, по сумме измерений превосходящие 120 см либо превосходящие хотя бы по одному измерению 60 см, считаются крупногабаритными. Наша посылка имеет размеры 49×28×39 см, значит, она не крупногабаритная.
Расстояние между городами по железной дороге 485 км, следовательно, в таблице работаем с первой колонкой, где указано расстояние менее 600 км, тариф за массу там 194 рубля, а далее дополнительно оплачиваются каждые полные / неполные 500 г по 22 рубля. То есть 19 кг=19000 гр, уберем 500 гр, за которые заплатим 194 руб, получим, 18500 гр. Теперь 18500: 500=37. Это столько раз по 22 рубля надо дополнительно заплатить: 22∙37=814 рублей. Итак, 814+194=1008 руб.
Мы определили, что посылка тяжеловесная, следовательно, идет наценка 40%, вспомним, чтобы найти процент от числа, надо выразить его десятичной дробью и умножить на данное число, то есть: 0,4∙1008=403,2 – это наценка. Прибавляем ее к найденной сумме 1008 руб, получаем 1411,2 рубля стоит отправление посылки.
Ответ: 1411,2 рубля
Задание №8
Отметьте на координатной прямой число √166
![]()
На координатной прямой нам показаны целые числа, а показать надо иррациональное. Поэтому представим некоторые числа на луче в виде квадратного корня, то есть возведем в квадрат.

Теперь видно, что данное число будет располагаться между 12 и 13, ближе к числу 13. Покажем это на координатной прямой.
![]()
Расположение данного числа на координатной прямой – это и есть наш ответ.
Задание №9
Найдите значение выражения 4(4а4)2а3а7 при а=√20
Чтобы найти значение данного выражения, необходимо его сначала упростить, а уже потом подставить значение переменной а.
Для упрощения вспомним свойства степеней: при возведении степени в степень показатели умножают, а основание оставляют прежним; при умножении степеней показатели складывают, при делении – вычитают, показатели также оставляем такими же.
В нашем случае имеем дробь, в числителе и знаменателе которой есть действия со степенями. Возводим в числителе в квадрат каждый множитель из скобок, в знаменателе выполняем умножение степеней (складываем показатели):
4(4а4)2а3а7=4∙16а8а10
Далее в числителе выполняем умножение чисел 4 и 16:
4(4а4)2а3а7=4∙16а8а10=64а8а10
Теперь надо сократить числитель и знаменатель на меньшую степень, то есть на а8:
4(4а4)2а3а7=4∙16а8а10=64а8а10=64а2
Подставляем вместо переменной «а» её значение √20:
4(4а4)2а3а7=4∙16а8а10=64а8а10=64а2=64(√20)2
По правилу возведения во вторую степень квадратного корня, получаем в знаменателе 20. Далее выполняем деление 64 на 20 и получаем ответ 3,2
4(4а4)2а3а7=4∙16а8а10=64а8а10=64а2=64(√20)2=6420=3,2
Ответ: 3,2
Найдите значение выражения: 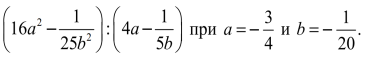
Чтобы найти значение данного выражения, надо его сначала упростить, а уже затем подставить значения данных переменных.
Дано выражение, содержащее действия в скобках, при этом это действия с дробными рациональными выражениями, содержащими степень.
Удобнее выполнять каждое действие отдельно. По порядку действий сначала выполняются действия в скобках – вычитания, а затем уже деление.
В первом действии находим общий знаменатель, это 25в2. Дополнительный множитель к числу 16а2 будет 25в2.
16а2−125в2=16а2∙25в2−125в2
Перемножим числа 16 и 25, получим выражение:
16а2−125в2=16а2∙25в2−125в2=400а2в2−125в2
Выполняем второе действие, в котором приводим к общему знаменателю 5в и находим дополнительный множитель к выражению 4а:
4а−15в=4а∙5в−15в
Перемножим числа 4 и 5, получим выражение:
4а−15в=4а∙5в−15в=20ав−15в
Последнее действие – деление рациональных дробей. Сразу же раскладываем на множители числитель первой дроби по формуле сокращенного умножения (разность квадратов двух выражений), то есть а2−в2=(а−в)(а+в) . При делении дробей надо умножить делимое на дробь, обратную делителю. Получим выражение:
400а2в2−125в2: 20ав−15в=(20ав−1)(20ав+1)25в2∙5в20ав−1
В полученном выражении сокращаем числитель и знаменатель на (20ав−1)и на 5в
400а2в2−125в2: 20ав−15в=(20ав−1)(20ав+1)25в2∙5в20ав−1=20ав+15в
Теперь надо подставить значения переменных, данных по условию, затем выполнить решение данного выражения:
20ав+15в=20∙(−34)∙(−120)+15∙(−120)=34+1−14=134−14=74∙(−41)=−7
В решении видно, что в числителе при умножении сократились 20, не стало минусов, так как умножали два отрицательных числа. В знаменателе при умножении сократили на 5, знаменатель получили отрицательный. Затем выполнили сложение 34 и 1, перевели полученное смешанное число в неправильную дробь. Выполнили деление двух обыкновенных дробей и сократили при умножении на 4. Получили ответ −7.
Ответ: −7
Задание №10
В коробке лежат одинаковые на вид шоколадные конфеты: 5 с карамелью, 3 с орехами и 2 без начинки. Коля наугад выбирает одну конфету. Найдите вероятность того, что он выберет конфету без начинки.
Задание по теории вероятности. Разбираемся, что у нас известно по условию задачи:
С карамелью – 5
С орехами – 3
Без начинки – 2
Имеем разные конфеты, а выбрать надо конфету без начинки. То есть количество элементарных исходов, то есть общее количество равно 5+3+2=10. А количество благоприятных исходов, то есть, что Коля выберет конфету без начинки, равно 2, так как по условию их 2. Теперь находим вероятность, для этого количество благоприятных исходов делим на общее количество конфет: 2:10=0,2
Ответ: 0,2
В среднем 12 керамических горшков из 200 после обжига имеют дефекты. Найдите вероятность того, что случайно выбранный после обжига горшок не имеет дефекта.
Задание по теории вероятности. Разбираемся, что у нас известно по условию задачи:
Всего – 200 горшков
С дефектами – 12 горшков
Найти надо вероятность того, что случайно выбранный горшок не имеет дефекта, значит, находим сначала, сколько горшков без дефекта: 200-12=188. Теперь находим вероятность, то есть количество благоприятных исходов (без дефекта) делим на общее количество: 188:200=0,94
Ответ: 0,94
Задание №11
Турист прошёл 20% всего маршрута, а затем 25% оставшегося расстояния. Сколько километров нужно ещё пройти туристу, если длина всего маршрута составляет 132 км?
Для решения данной задачи можно составить схему, тогда будет видно полное условие. Весь путь по условию – 132 км, покажем это как 100%. Турист прошел 20% пути, значит, осталось пройти 80%, покажем это на схеме. Затем он прошел 25% уже оставшегося пути, то есть от оставшихся 80% пути. Покажем вопросом то, что требуется найти.
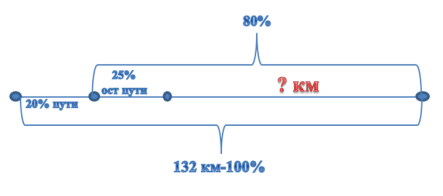
Если туристу после 20% пути, который он прошел, осталось 80%, то можно найти, сколько это километров, так как общий путь 132 км. При нахождении процента от числа переводим проценты в десятичную дробь (разделим на 100) и умножим на данное число: 0,8∙132=105,6 км
Теперь, зная, что он прошел 25% от этого пути, то есть от 105,6 км, то останется пройти ему 100%-25%=75%. Найдем 75% от 105,6 км. Выражаем проценты десятичной дробью и умножаем на данное число: 0,75∙105,6=79,2 км.
Значит, 79,2 км осталось пройти туристу.
Ответ: 79, 2 км
Бак автомобиля вмещает 95 л бензина. Перед поездкой бак был заполнен бензином на 80%. За время поездки было израсходовано 25% бензина. Сколько литров бензина нужно долить, чтобы бак стал полным?
Если бак вмещает 95 литров, а был заполнен на 80%, значит, мы можем найти, на сколько литров был заполнен бак. Находим 80% от числа 95, то есть выражаем проценты десятичной дробью и умножаем на данное число: 0,8∙95=76 литров.
Теперь, зная, что истратили 25%, а это четвертая часть, найдем, сколько бензина истратили: 76:4=19 литров.
Значит, осталось в баке 76-19=57 литров.
По условию требуется найти, сколько бензина нужно долить, чтобы бак стал полным. Следовательно, 95-57=38 литров требуется долить в бак.
Ответ: 38 литров
Задание №12
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм ABCD. Найдите произведение стороны AD и высоты параллелограмма, проведённой к этой стороне.
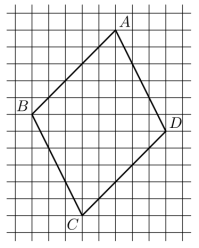
Для решения надо выполнить дополнительные построения, так как сосчитать количество клеток стороны АД и высоты невозможно.
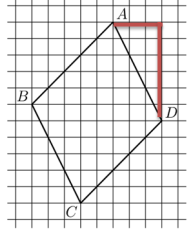 |
Достроили до прямоугольного треугольника. Теперь можно найти по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) сторону АД. Посчитаем длины катетов по клеточкам: 3 и 6. Составляем равенство по теореме Пифагора:
АД=√32+62=√45 |
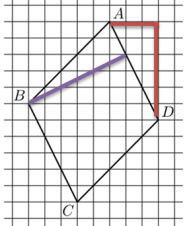 |
Теперь надо провести высоту на сторону АД. Но мы не можем сосчитать её длину. Поэтому выполним снова дополнительное построение – до прямоугольного треугольника. |
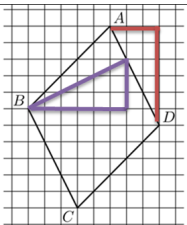 |
Получили новый прямоугольный треугольник, у которого считаем клеточки – длины катетов, это опять 3 и 6. Значит, высота равна стороне, то есть √45
Теперь можно ответить на вопрос задачи – найти произведение стороны AD и высоты параллелограмма, проведённой к этой стороне: √45 ∙√45=45 Ответ: 45 |
На клетчатой бумаге с размером клетки 1 1× изображён острый угол. Найдите тангенс этого угла.
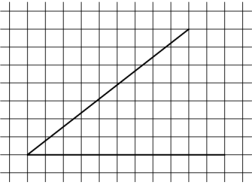
Для решения задачи надо вспомнить определение тангенса: тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Из определения следует, что необходимо провести дополнительное построение до прямоугольного треугольника, посчитать длины катетов и составить отношение. Выполним построение, взяв на стороне угла точку так, чтобы она находилась в узле клетки. Опустим из неё перпендикуляр на другую сторону угла, получим прямоугольный треугольник, где длина противолежащего катета равна 3, а прилежащего 4.
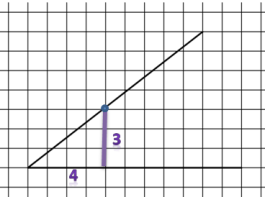
Составим отношение для нахождения тангенса: tq A=34=0,75
Ответ: 0,75
Задание №13
Углы треугольника относятся как 3:5:7. Найдите больший из этих углов. Ответ дайте в градусах.
Данная задача на отношение частей. Кроме этого, надо вспомнить, чему равна сумма углов треугольника. Сумма углов треугольника равна 180 градусов.
Примем за части данные из условия, то есть если углы треугольника относятся как 3:5:7 соответственно, то получается, что первый угол составляет 3 части от общей суммы углов, второй – 5, соответственно третий – 7 частей. Значит, всего частей было 15. Зная, что сумма углов треугольника равна 180 градусов, можно найти, сколько градусов приходится на 1 часть: 180:15=12. Теперь найдем, сколько градусов приходится на 7 частей, так как по условию задачи требуется найти величину наибольшего угла: 12∙7=84.
Ответ: 84
Один из углов равнобедренного тупоугольного треугольника на 69° больше другого. Найдите больший угол этого треугольника. Ответ дайте в градусах.
Для решения данной задачи надо вспомнить определение равнобедренного треугольника и его свойства. Итак, равнобедренным называется треугольник, у которого две стороны равны. Углы при основании равнобедренного треугольника равны. Ну и вспомним, что сумма углов треугольника равна 180 градусов.
По условию задачи нам сказано, что один из углов равнобедренного тупоугольного треугольника на 69° больше другого, следовательно, этот угол не при основании. Обозначим угла при основании за «х», тогда угол, который на 69 градусов больше, будет равен х+69.
Зная, что сумма углов треугольника 180 градусов, а угла при основании равны, составим и решим уравнение:
х+х+х+69=180
3х=180-69
3х=111
х=111:3
х=37
Значит, углы при основании равны по 37 градусов. Следовательно, больший угол равен 37+69=106 градусов
Ответ: 1060
Задание №14
Выберите верные утверждения и запишите в ответе их номера.
- Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники могут быть не равны.
- Через любые три различные точки плоскости, не лежащие на одной прямой, можно провести окружность.
- В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов
Проверяем истинность каждого утверждения и находим верные для ответа
Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники могут быть не равны.
Мы знаем первый признак равенства треугольников, который звучит так: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. У нас же в утверждении сказано, что такие треугольники могут быть не равны, и не указано, про какой именно угол идет речь. Следовательно, это верное утверждение.
Через любые три различные точки плоскости, не лежащие на одной прямой, можно провести окружность.
Это верное утверждение, так как данные точки можно соединить и получится треугольник, а мы знаем, что около любого треугольника можно описать окружность, то есть она будет проходить через все его вершины, а это значит – через данные три точки, которые не лежат на одной прямой.
В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. Это неверное утверждение, так как по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, а у нас в утверждении — разности.
Ответ: 12
Выберите неверное утверждение и запишите в ответе его номер.
- Центром окружности, вписанной в любой треугольник, является точка пересечения медиан этого треугольника.
- Диагонали параллелограмма точкой их пересечения делятся пополам.
- Если две прямые перпендикулярны третьей, то эти две прямые параллельны.
Проверяем каждое утверждение на истинность и находим НЕВЕРНОЕ, так как именно его номер надо указать в ответе.
Центром окружности, вписанной в любой треугольник, является точка пересечения медиан этого треугольника. Это неверное утверждение, так по теореме центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Диагонали параллелограмма точкой их пересечения делятся пополам. Это верное утверждение, так как это свойство диагоналей параллелограмма.
Если две прямые перпендикулярны третьей, то эти две прямые параллельны. Это верное утверждение, так как это признак параллельности прямых
Ответ: 1
Задание №15
Механический одометр (счётчик пройденного пути) для велосипеда — это прибор, который крепится на руле и соединён тросиком с редуктором, установленным на оси переднего колеса. При движении велосипеда спицы колеса вращают редуктор, это вращение по тросику передаётся счётчику, который показывает пройденное расстояние в километрах. У Антона был велосипед с колёсами диаметром 16 дюймов и с одометром, который был настроен под данный диаметр колеса. Когда Антон вырос, ему купили дорожный велосипед с колёсами диаметром 20 дюймов. Антон переставил одометр со своего старого велосипеда на новый, но не настроил его под диаметр колеса нового велосипеда. В воскресенье Антон поехал кататься на велосипеде в парк. Когда он вернулся, одометр показал пройденное расстояние — 13,2 км. Какое расстояние на самом деле проехал Антон?
Разбираемся с условием, что мы знаем: был велосипед с колёсами диаметром 16 дюймов, купили новый велосипед с колёсами диаметром 20 дюймов. Имеется специальный прибор, который переставили, но не настроили, проехав 13,2 км. И это расстояние не реальное, его показал не настроенный прибор.
Надо понимать, что большое колесо сделает меньше оборотов, чем маленькое, проехав то же расстояние. Количество оборотов колеса и, значит, показания счётчика километров обратно пропорциональны диаметру колеса.
Запишем решение в бланк, составляя пропорцию:
Пусть «х» реальное расстояние, тогда
х13,2=2016
х=20∙13,2:16=16,5 км
Значит, 16,5 км реальное расстояние, которое проехал Антон на самом деле
Ответ: 16,5 км
Квадратный лист бумаги ABCD согнули по линии EF так, что точка C попала на середину стороны AD (точка С1 на рисунке). Найдите длину отрезка DE, если длина стороны листа равна 16 см. Ответ дайте в сантиметрах. Запишите решение и ответ.
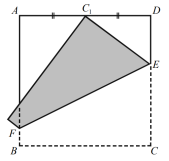
Рассмотрим треугольник С1ДЕ, где угол Д прямой по условию, С1Д=16:2=8 см, так как по условию сказано, что точка C попала на середину стороны AD (точка С1 на рисунке).
Запишем равенство по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов): ЕС12=С1Д2+ДЕ2. Но так как ЕС1=16-ДЕ, то подставим это в наше равенство:
(16-ДЕ)2=82+ДЕ2
Возведем левую часть в квадрат по формуле квадрата разности двух выражений:
256-32ДЕ+ДЕ2=64+ДЕ2
Приведем подобные, взаимоуничтожив в разных частях слагаемые ДЕ2, получим:
256-32ДЕ=64
Дорешаем равенство, перенося слагаемые и изменяя у них знаки на противоположные:
256-64=32ДЕ
192=32ДЕ
ДЕ=6
Ответ: 6
Возможно другое объяснение решения задачи.
Задание №16
Чемпионаты мира по футболу проводятся с 1930 года раз в четыре года. Чтобы попасть в финальную часть чемпионата сначала национальные команды соревнуются в отборочных турнирах. Финальная часть чемпионата мира начинается с группового этапа. Команды разбиваются на 8 групп, по четыре команды в каждой, и играют между собой в группах. По две лучших команды из каждой группы, всего 16 команд, выходят в заключительную стадию чемпионата, которая называется «плей-офф». Сначала проходят восемь игр этапа «1/8 финала». Проигравшие выбывают, а победители выходят в следующий этап — «1/4 финала». На этом этапе проигравшие также выбывают, а победители выходят в «полуфинал». Таким образом, в полуфинале проводится два матча. Победители полуфинальных матчей могут продолжить борьбу в финальном матче за первое и второе места, а проигравшие встречаются в игре за третье и четвёртое места. Чемпионат мира по футболу 2014 года проходил в Бразилии. Лучшими командами турнира стали сборные Аргентины, Бразилии, Германии и Нидерландов. Каждая из них к моменту финальных игр сыграла по 6 матчей: по 3 матча в групповом этапе и по 3 матча в плей-офф. В таблице показано количество мячей, забитых командами Аргентины, Германии и Нидерландов в первых шести играх чемпионата мира 2014 года. Рассмотрите таблицу и прочтите фрагмент сопровождающей статьи.
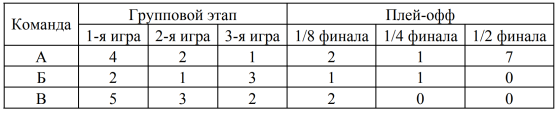
Среди всех команд, вышедших в полуфинал, наименьшее число мячей в групповом этапе забила сборная Аргентины, а наибольшее — сборная Нидерландов. Немцы же установили рекорд по количеству мячей, забитых за одну игру. Сборная Бразилии первые шесть игр чемпионата провела не блестяще. Во второй игре бразильцы не забили ни одного мяча и забили всего лишь по одному мячу в 1/8 финала и в полуфинале. Правда, в первом своём матче сборная Бразилии трижды поразила ворота противника, а в третьем — четыре раза. Общее количество мячей, забитых Бразилией во всех шести играх, равно 11.
- На основании прочитанного определите, какой сборной соответствует строка В.
- По имеющемуся описанию заполните таблицу, показывающую количество голов, забитых сборной Бразилии в первых шести матчах чемпионата мира 2014 года.

В тексте сказано, что среди всех команд, вышедших в полуфинал, наименьшее число мячей в групповом этапе забила сборная Аргентины, а наибольшее — сборная Нидерландов. Немцы же установили рекорд по количеству мячей, забитых за одну игру. Посчитаем количество мячей в строке А группового этапа: 4+2+1=7, в строке Б: 2+1+3=6, в строке В: 5+3+2=10. Получаем, что наибольшее количество очков в строке В, а это мячи Нидерландов, так как по условию они забили наибольшее количество.
Ответ: Нидерланды
По имеющемуся описанию надо заполнить таблицу, показывающую количество голов, забитых сборной Бразилии в первых шести матчах чемпионата мира 2014 года.
Читаем описание и заполняем таблицу: Сборная Бразилии первые шесть игр чемпионата провела не блестяще. Во второй игре бразильцы не забили ни одного мяча (ставим нуль во 2-й игре) и забили всего лишь по одному мячу в 1/8 финала и в полуфинале (ставим единицы в столбцах 1/8 и ½). Правда, в первом своём матче сборная Бразилии трижды поразила ворота противника (ставим тройку в столбце 1-я игра), а в третьем — четыре раза (ставим четверку в столбце 3-я игра). Общее количество мячей, забитых Бразилией во всех шести играх, равно 11 (значит, посчитаем, сколько мы уже поставили: 3+0+4+1+1=9; тогда до 11 мячей не хватает 2, поэтому ставим двойку в столбец ¼ финала).
Ответ:
| Команда | Групповой этап | Плей-офф | ||||
| 1-я игра | 2-я игра | 3-я игра | 1/8 финала | ¼ финала | ½ финала | |
| Бразилия | 3 | 0 | 4 | 1 | 2 | 1 |
Чемпионаты мира по футболу проводятся с 1930 года раз в четыре года. Чтобы попасть в финальную часть чемпионата сначала национальные команды соревнуются в отборочных турнирах. Финальная часть чемпионата мира начинается с группового этапа. Команды разбиваются на 8 групп, по четыре команды в каждой, и играют между собой в группах. По две лучших команды из каждой группы, всего 16 команд, выходят в заключительную стадию чемпионата, которая называется «плей-офф». Сначала проходят восемь игр этапа «1/8 финала». Проигравшие выбывают, а победители выходят в следующий этап — «1/4 финала». На этом этапе проигравшие также выбывают, а победители выходят в «полуфинал». Таким образом, в полуфинале проводится два матча. Победители полуфинальных матчей могут продолжить борьбу в финальном матче за первое и второе места, а проигравшие встречаются в игре за третье и четвёртое места. Чемпионат мира по футболу 1990 года проходил в Италии. Лучшими командами турнира стали сборные Англии, Аргентины, Германии и Италии. Каждая из них к моменту финальных игр сыграла по 6 матчей: по 3 матча в групповом этапе и по 3 матча в плей-офф. В таблице показано количество мячей, забитых командами Англии, Аргентины и Германии в первых шести играх чемпионата мира 1990 года. Рассмотрите таблицу и прочтите фрагмент сопровождающей статьи.
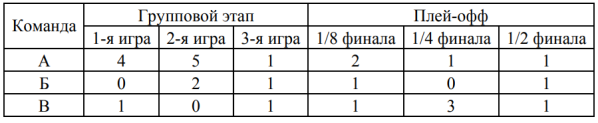
Среди всех команд, вышедших в полуфинал, наименьшее число мячей в групповом этапе забила Англия, а наибольшее — сборная Германии. Аргентинцы же забили меньше всего голов по итогам всех шести игр. Сборная Италии лучшие свои результаты показала в третьей игре группового этапа и в 1/8 финала, забив в каждом из этих матчей по 2 мяча. Общее количество мячей, забитых сборной Италии во всех шести играх, равно 8, при этом не было матча, в котором итальянцы ни разу не смогли отправить мяч в ворота соперника.
- На основании прочитанного определите, какой сборной соответствует строка В.
- По имеющемуся описанию заполните таблицу, показывающую количество голов, забитых сборной Италии в первых шести матчах чемпионата мира 1990 года.

Необходимо определить, какой сборной соответствует строка В. Читаем текст и определяем: Среди всех команд, вышедших в полуфинал, наименьшее число мячей в групповом этапе забила Англия, а наибольшее — сборная Германии. Аргентинцы же забили меньше всего голов по итогам всех шести игр.
Считаем мячи в групповом этапе. В строке А: 4+5+1=10; в строке Б: 0+2+1=3; в строке В: 1+0+1=2. Таким образом, наименьшее количество получилось в строке В, а это сборная Англии.
Ответ: Англия
По имеющемуся описанию надо заполнить таблицу, показывающую количество голов, забитых сборной Италии в первых шести матчах чемпионата мира 1990 года.
Читаем текст заполняем таблицу:
Сборная Италии лучшие свои результаты показала в третьей игре группового этапа и в 1/8 финала, забив в каждом из этих матчей по 2 мяча (ставим по двойке в столбцы 3-я игра и 1/8 финала). Общее количество мячей, забитых сборной Италии во всех шести играх, равно 8, при этом не было матча, в котором итальянцы ни разу не смогли отправить мяч в ворота соперника (значит, нет нулей в оставшихся столбцах. А так как всего было забито 8 мячей, значит, в оставшихся четырех столбцах надо поставить по единице, так как 1+1+2+2+1+1=8).
Ответ:
| Команда | Групповой этап | Плей-офф | ||||
| 1-я игра | 2-я игра | 3-я игра | 1/8 финала | ¼ финала | ½ финала | |
| Италия | 1 | 1 | 2 | 2 | 1 | 1 |
Задание №17
В прямоугольной трапеции ABCD с основаниями AD и BC диагональ АС является биссектрисой угла А, равного 450. Найдите длину диагонали BD, если меньшее основание трапеции равно 3√2 .
Для решения задачи необходимо сделать чертеж с указанием необходимых данных.
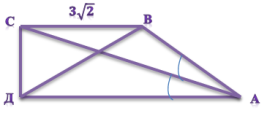
Н |
В данной трапеции угол АСВ равен углу ДАС как накрест лежащие при параллельных прямых ВС и АД и секущей АС. Так как по условию АС биссектриса угла А, то угол ВСА равен углу ВАС, следовательно треугольник АВС равнобедренный, то есть АВ=ВС=3√2. |
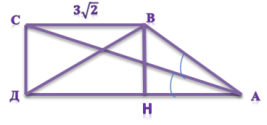 |
Выполним дополнительное построение – проведем высоту ВН на сторону АД.
Рассмотрим прямоугольный треугольник АВН, где угол А по условию 45 градусов, значит, угол НВА тоже равен 45 градусов (сумма острых углов прямоугольного треугольника равна 90 градусов). Значит, треугольник АВН равнобедренный и АН=ВН. Так как АВ=3√2, то можно найти по теореме Пифагора высоту ВН. АВ2=ВН2+АН2 (3√2)2=х2+х2 18=2х2 х2=9, следовательно х=3, то есть высота ВН=3. Так как трапеция прямоугольная, то СД=ВН=3. Теперь рассмотрим прямоугольный треугольник ВСД, где ВС=3√2, СД=3. По теореме Пифагора ВД2=(3√2)2+32=18+9=27, значит, ВД=√27 ВД=3√3 Ответ: ВД=3√3 |
Допускается другое расположение чертежа, другая последовательность решения, которая приведет к правильному ответу.
В треугольнике АВС стороны АВ и АС равны. На стороне АС взяли точки Х и Y так, что точка Х лежит между точками А и Y и AX=BX=BY. Найдите величину угла CBY, если ∠ XBY =280 . Запишите решение и ответ.
Для решения задачи выполним построение чертежа.
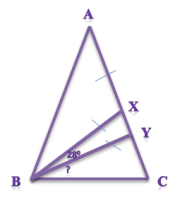 |
Рассмотрим равнобедренный по построению треугольник BXY, где BX=ВY, угол XВY=280. Можно найти углы при основании (по свойству они равны):
(1800-280):2=152:2=760. Итак, углы BYX и BXY равны по 760. В равнобедренном треугольнике АВХ можно найти угол АХВ, так как он является смежным с углом BXY. Зная, что сумма смежных углов равна 180 градусов, найдем величину угла АХВ, 1800-760=1040. Значит углы А и ХВА равны (1800-1040):2=380. Так как треугольник АВС тоже равнобедренный, то найдем величину углов при основании: (1800-380):2=710 Теперь найдем искомый по условию задачи угол СВY: 710-280-380=50 |
Возможно другое расположение построения чертежа, а также другая последовательность решения, приводящая к правильному результату.
Ответ: 50
Задание №18
Катер прошёл по течению реки 40 км, повернув обратно, он прошёл ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость катера, если скорость течения реки равна 5 км/ч. Ответ дайте в км/ч. Запишите решение и ответ.
Для решения задачи составим таблицу с величинами – скорость, время, расстояние. Так как найти надо собственную скорость катера, то примем эту величину за «х». Зная, что скорость по течению находится путем сложения скоростей по течению и скорости течения, а скорость против течения вычитанием, запишем эти действия в таблицу. Заполним столбец «расстояние», оно известно по условию. Так как время находится делением расстояния на скорость, то заполним в таблице столбец «время».
Данную таблицу и все последующие решения записать в поле «решение» бланка ВПР:
| Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| По течению | х+5 | 40х+5 | 40 км |
| Против течения | х-5 | 30х−5 | 30 км |
| Собственная | х, х>0 | ||
| Течения | 5 |
Зная, что катер затратил на весь путь 5 часов, составим и решим уравнение:
40х+5+30х−5=5
40(х−5)+30(х+5)=5(х−5)(х+5)
40х−200+30х+150=5х2−125
5х2−70х−125+50=0
5х2−70х−75=0, (:5)
х2−14х−15=0
По теореме Виета х1=−1, х2=15. Так как скорость — это положительная величина, то собственная скорость катера равна 15 км/ч.
Ответ: 15 км/ч
Пояснение к решению уравнения: уравнение дробно-рациональное, привели к общему знаменателю, и нашли дополнительные множители; привели подобные слагаемые, получили квадратное уравнение, которое можно решать как с помощью теоремы Виета, так и найти корни по формуле через дискриминант.
Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.
Первый рабочий за час делает на 6 деталей больше, чем второй, и выполняет заказ, состоящий из 90 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий? Запишите решение и ответ.
По условию задачи требуется найти количество деталей, изготовленных за 1 час вторым рабочим. Обозначим за «х» это количество. Так как первый рабочий за час делает на 6 деталей больше, то (х+6) – это количество деталей, изготовленных за час первым рабочим.
Так как каждый из них должен сделать 90 деталей, то производительность труда первого будет 90х+6, а второго 90х. Зная, что первый рабочий выполняет заказ на 4 часа быстрее, составим и решим уравнение:
90х+6+4=90х
90х+4х(х+6)=90(х+6)
90х+4х2+24х=90х+540
4х2+24х−540=0 (:4)
х2+6х−135=0
D=b2−4ac=36−4(−135)=36+540=576>0, 2 корня
х1=−b−√D2a=−6−242=−302=−15 посторонний корень
х2=−b+√D2a=−6+242=182=9
Значит, 9 деталей в час изготавливает второй рабочий.
Ответ: 9 деталей.
Задание №19
На товарищеском турнире школьников по шахматам каждый школьник сыграл с каждым другим не более одной партии, кроме того, каждый из них сыграл с приглашённым гроссмейстером не более одной партии. Всего было сыграно 56 партий. Какое наименьшее количество школьников могло участвовать в этом турнире? Запишите решение и ответ.
В данной задаче очень мало данных для решения, поэтому введем переменную «х», обозначив ею количество всех участников, но не считая гроссмейстера. Тогда количество партий, которые сыграл гроссмейстер, не больше «х», а количество партий между школьниками не больше, чем х(х−1)2.
Получается, что общее количество партий не превосходит х+х(х−1)2
Получаем неравенство х+х(х−1)2≥56
Подставим вместо «х» числа.
Итак, при x 1 получится неверное неравенство, так как 1+1(1−1)2≥56, тогда
1≥56.
Если x 2 получаем 2+2(2−1)2≥56, тогда 3≥56. Это тоже неверное неравенство.
Попробуем подставить числа больше, например, 9. Получим 9+9(9−1)2≥56, тогда 45≥56. Неверное неравенство.
При х=10 получим 55≥56.
При х=11 получим, что 66≥56. Это верное неравенство и мы получили наименьшее натуральное число, которое требуется найти по условию задачи.
Ответ: 11
Возможна другая последовательность логических рассуждений, приводящая к верному ответу.
Митя написал пять натуральных (необязательно различных) чисел, а потом Таня вычислила все возможные попарные суммы этих чисел. Получилось всего три различных значения: 77, 88 и 99. Посмотрев на полученные Таней значения, Петя смог точно назвать наибольшее из написанных Митей чисел. Какое это число? Запишите решение и ответ.
По условию задачи сказано, что числа натуральные и необязательно различные, значит, можно рассмотреть случай, что среди написанных чисел есть одинаковые. Тогда действительно, если все написанные числа разные, то различных попарных сумм должно быть не менее четырёх, например, суммы одного числа с четырьмя остальными. Следовательно, среди попарных сумм есть суммы двух одинаковых натуральных чисел. Такая сумма должна быть чётной, в нашем списке это число 88. Следовательно, среди написанных есть число 44 и оно написано не меньше двух раз. Одинаковых чисел, отличных от 44, быть не может, так как среди попарных сумм было бы ещё одно чётное число.
Обозначим одно из трёх оставшихся чисел за «х», тогда среди попарных сумм есть число (44+ x), значит, х равно либо 99−44=55, или 77−44=33. Наборы 44, 44, 44, 44, 55 и 44, 44, 44, 44, 33 нам не подходят, так как в них всего две различные попарные суммы. Значит, был написан набор 44, 44, 44, 33, 55. Нам надо определить наибольшее число, следовательно, наибольшее число — это 55.
Ответ: 55
Допускается другая логическая последовательность действий, приводящая к верному ответу.