В зависимости от конкретных чисел используется способ сравнения, но существует способ, который охватывает все числа, он основывается на следующем определении.
Пример №1.
- 123>118, так как 123–118=5, a 5>0;
- –15>–65, так как –15–(–65)= –15+65=50, a 50>0
- 118<123, так как 118–123=–5, a –5<0;
- –90<–50, так как –90–(–50)=–90+50=–40, а –40<0
- 451=451, так как 451–451=0
Пример №2.
- Дано неравенство 45>21. Если обе части умножим на одно и то же положительное число, например, 10, то получится верное неравенство 450>210.
- Дано неравенство 95>35. Обе части разделим на одно и то же отрицательное число (–5), при этом знак неравенства изменим на противоположный: 95:(–5)<35:(–5), получим верное неравенство –19<–7.
- Даны числа 17 и 52, где 17<52. Если разделить число 1 на каждое из них, то получим:
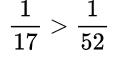 Это неравенство получим в соответствии со следствием из свойства №3.
Это неравенство получим в соответствии со следствием из свойства №3.
Текст: Алла Василевская, 7.2k 👀