Всероссийские проверочные работы (ВПР) проводятся в целях осуществления мониторинга результатов перехода на ФГОС и направлены на выявление качества подготовки обучающихся. Назначение КИМ для проведения проверочной работы по математике – оценить качество общеобразовательной подготовки обучающихся 6 классов в соответствии с требованиями ФГОС. КИМ ВПР позволяют осуществить диагностику достижения предметных и метапредметных результатов обучения, в том числе овладение межпредметными понятиями и способность использования универсальных учебных действий (УУД) в учебной, познавательной и социальной практике. Результаты ВПР в совокупности с имеющейся в общеобразовательной организации информацией, отражающей индивидуальные образовательные траектории обучающихся, могут быть использованы для оценки личностных результатов обучения. Результаты ВПР могут быть использованы образовательными организациями для совершенствования методики преподавания математики, муниципальными и региональными органами исполнительной власти, осуществляющими государственное управление в сфере образования, для анализа текущего состояния муниципальных и региональных систем образования и формирования программ их развития.
Содержание и структура проверочной работы определяются на основе Федерального государственного образовательного стандарта основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897) с учетом Примерной основной образовательной программы основного общего образования (одобрена решением Федерального учебно-методического объединения по общему образованию (протокол от 08.04.2015 № 1/15 (в редакции протокола № 1/20 от 04.02.2020)) и содержания учебников, включенных в Федеральный перечень.
Всероссийские проверочные работы основаны на системнодеятельностном, компетентностном и уровневом подходах. В рамках ВПР наряду с предметными результатами обучения учеников основной школы оцениваются также метапредметные результаты, в том числе уровень сформированности универсальных учебных познавательных, коммуникативных и регулятивных действий (УУД) и овладения межпредметными понятиями. Тексты заданий в вариантах ВПР в целом соответствуют формулировкам, принятым в учебниках, включенных в Федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.
Структура проверочной работы
Работа содержит 13 заданий. В заданиях 1–8, 10 необходимо записать только ответ. В задании 12 нужно изобразить рисунок или требуемые элементы рисунка. В заданиях 9, 11, 13 требуется записать решение и ответ.
Кодификатор проверяемых элементов содержания
| № п/п | Проверяемые элементы содержания |
| 1 | Числа и вычисления |
| 2 | Геометрические фигуры |
| 3 | Текстовые задачи |
| 4 | Статистика и теория вероятностей |
| 5 | Измерения и вычисления |
Типы заданий
- В заданиях 1–2 проверяется владение понятиями отрицательные числа, обыкновенная дробь.
- В задании 3 проверяется умение находить часть числа и число по его части.
- В задании 4 проверяется владение понятием десятичная дробь.
- Заданием 5 проверяется умение оценивать размеры реальных объектов окружающего мира.
- В задании 6 проверяется умение извлекать информацию, представленную в таблицах, на диаграммах.
- В задании 7 проверяется умение оперировать понятием модуль числа.
- В задании 8 проверяется умение сравнивать обыкновенные дроби, десятичные дроби и смешанные числа.
- В задании 9 проверяется умение находить значение арифметического выражения с обыкновенными дробями и смешанными числами.
- Задание 10 направлено на проверку умения решать несложные логические задачи, а также на проверку умения находить пересечение, объединение, подмножество в простейших ситуациях.
- В задании 11 проверяются умения решать текстовые задачи на проценты, задачи практического содержания.
- Задание 12 направлено на проверку умения применять геометрические представления при решении практических задач, а также на проверку навыков геометрических построений.
- Задание 13 является заданием повышенного уровня сложности и направлено на проверку логического мышления, умения проводить математические рассуждения.
Успешное выполнение обучающимися заданий 12 и 13 в совокупности с высокими результатами по остальным заданиям говорит о целесообразности построения для них индивидуальных образовательных траекторий в целях развития их математических способностей.
Система оценивания
Правильное решение каждого из заданий 1–8, 10, 12 оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину, изобразил правильный рисунок. Выполнение каждого из заданий 9, 11, 13 оценивается от 0 до 2 баллов. Максимальный первичный балл – 16.
Перевод первичных баллов в отметки по пятибалльной шкале
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичные баллы | 0–5 | 6–9 | 10–13 | 14-16 |
Задание №1
Вычислить: –34+18•3
В данном примере два действия. Выполним первое – умножение, 18 умножим на 3, получим 54. Далее у нас получается действие: –34+54. По правилу нам надо выполнить вычитание, так как два числа имеют разные знаки. Из числа, модуль которого больше, — это 54, вычтем число, которое по модулю меньше – это 34, получим в ответе положительное число 20 (так как 54 – положительное и оно по модулю больше).
Ответ: 20
Вычислить: –24+72:4
В данном примере два действия. Выполним первое – деление, 72 разделим на 4, получим 18. Далее у нас получается действие: –24+18. По правилу нам надо выполнить вычитание, так как два числа имеют разные знаки. Из числа, модуль которого больше, — это 24, вычтем число, которое по модулю меньше – это 18, получим в ответе отрицательное число 6 (так как 24 – отрицательное и оно по модулю больше).
Ответ: –6
Вычислить: 27 – 13∙(−5)
В данном примере два действия. Выполним первое – умножение, 13 умножим на (−5), получим (−65).
Далее у нас получается действие: 27–(–65). По правилу вычитания отрицательного числа нам надо выполнить сложение, так как, раскрывая скобки, перед которыми стоит знак минус, надо изменить знак у числа в скобках на противоположный, то есть получим 27+65. Выполним сложение и получим ответ 92.
Можно рассуждать по-другому: выполним умножение чисел минус 13 и минус 5, получим положительное число 65, то есть 27−13∙(−5)=27+65=92
Ответ: 92
Задание №2
Вычислить: 1−58:2532
В данном примере два действия. Выполним первое – деление. По правилу деления обыкновенных дробей надо делимое умножить на число обратное делителю. Запишем это так:
58:2532=58∙3225
Теперь выполним умножение обыкновенных дробей, предварительно сократив 8 и 32 на 8, а 5 и 25 на 5. Получим:
58∙3225=11∙45=45
Теперь выполним второе действие – вычитание дроби из 1. Вспомним, чтобы вычесть из 1, необходимо представить её в виде обыкновенной неправильной дроби, числитель и знаменатель которой равны знаменателю второй дроби: 1−45= 55−45=15.
Ответ: 15
Вычислить: 35:(45+1120)
Решение
В данном примере два действия. Выполним первое – в скобках, вспомним правило сложения обыкновенных дробей с разными знаменателями: надо найти общий знаменатель, для чисел 5 и 20 это будет 20, так как это наименьшее число, которое делится и на 5 и на 20 одновременно. Затем найти дополнительный множитель к дроби 45 (надо 20:5, получим 4) и умножить его на числитель 4. После этого сложить числители, а знаменатель оставить тот же. Распишем данное действие:
45+1120=1620+1120=2720
Теперь выполняем деление. По правилу деления обыкновенных дробей надо делимое умножить на число обратное делителю. Запишем это так:
35:2720=35∙2027
Теперь выполним умножение обыкновенных дробей, предварительно сократив 3 и 27 на 3, а 5 и 20 на 5. Получим:
35:2720=35∙2027=11∙49=49
Ответ:49
Конец решения
Задание №3
Задумали число. Из 286 вычли утроенное задуманное число и получили седьмую часть задуманного числа. Найдите задуманное число.
Решить данное задание можно с помощью уравнения, обозначив задуманное число буквой х. Затем, следуя условию, составляем уравнение:
Из числа 286 вычли утроенное задуманное число, то есть пишем выражение 286 – 3х. Получили седьмую часть задуманного числа, то есть данное выражение 286−3х=17х (так как седьмая часть от х это и есть 17х). Теперь решаем данное уравнение, следуя алгоритму и правилам решения:
Переносим слагаемые с переменной в левую часть, без переменной в правую часть уравнения, изменяя у слагаемых при переносе знаки на противоположные:
−3х− 17х=−286
Приводим подобные слагаемые, которые есть в левой части уравнения, получим: −317х=−286
Находим неизвестный множитель действием деления, при этом смешанное число переведем в неправильную дробь:
х=−286:(−227)
От деления перейдем к умножению, так как по правилу деления на обыкновенную дробь надо делимое умножить на число обратное делителю.
х=−286∙(−722)
Выполним умножение и получим, что х=91. Ответ получили положительный, следуя правилу умножения двух отрицательных чисел. Итак, задуманное число равно 91.
Ответ: 91
Если от задуманного числа отнять 12, то получится число, которое в четыре раза меньше этого задуманного числа. Найдите задуманное число.
Решить данное задание можно с помощью уравнения, обозначив задуманное число буквой х. Затем, следуя условию, составляем уравнение:
Если от задуманного числа отнять 12, то есть составляем выражение х−12, то получится число, которое в 4 раза меньше задуманного, то есть данное выражение х−12 будет равно 14х. Получим уравнение:
х−12=14х
Теперь решаем данное уравнение, следуя алгоритму и правилам решения:
Переносим слагаемые с переменной в левую часть, без переменной в правую часть уравнения, изменяя у слагаемых при переносе знаки на противоположные:х−14х=12
Приводим подобные слагаемые в левой части уравнения:
34х=12
Находим неизвестный множитель действием деления:
х=12:34
От деления перейдем к умножению, так как по правилу деления на обыкновенную дробь надо делимое умножить на число обратное делителю:
х=12∙43
Выполним умножение и получим, что х=16. Итак, задуманное число равно 16.
Ответ: 16
Задание №4
Вычислите: −8,8+6,5∙1,6
В данном примере два действия, встречаются отрицательные числа. Выполним первое действие – умножение десятичных дробей, то есть получим −8,8+6,5∙1,6=−8,8+10,4. Теперь у нас есть два числа с разными знаками, поэтому, по правилу нам надо выполнить вычитание. Из числа, модуль которого больше, — это 10,4, вычтем число, которое по модулю меньше – это 8,8, получим в ответе положительное число 1,6 (так как 10,4 – положительное и оно по модулю больше).
Ответ: 1,6
Вычислите: (−8,9+1,5):3,7
В данном примере два действия, встречаются отрицательные числа. Выполним первое действие – в скобках. Там у нас два числа с разными знаками, поэтому, по правилу нам надо выполнить вычитание. Из числа, модуль которого больше, это 8,9 вычтем число, которое по модулю меньше – это 1,5. Получаем отрицательное число, так как 8,9 по модулю больше:
(−7,4):3,7
Теперь выполним деление десятичных дробей, перенеся запятые на одну цифру вправо в обоих множителях, так как у делителя после запятой одна цифра. Ответ будет отрицательным, так как выполняем деление двух чисел с разными знаками:
(−7,4):3,7=−74:37=−2
Ответ: -2
Задание №5
На рисунке изображены здание и стоящее рядом дерево. Высота дерева равна 10 м. Какова примерная высота здания? Ответ дайте в метрах.

В данном задании надо оценить размеры реальных объектов окружающего мира – здания и дерева. Нам известна высота дерева – 10 метров. Дом состоит из семи этажей, фундамента (нижняя часть, основание дома) и крыши. Фундамент примерно в два с половиной раза меньше одного этажа, а высота крыши примерно равна одному этажу дома. Если сравнить докуда доросло дерево, то видно, что оно на уровне четвертого этажа. Выше него еще три этажа и крыша, которая, как мы предположили, примерно равна одному этажу. Поэтому, высота дома может быть примерно равна двум размерам высоты дерева, то есть 10+10=20 метров. Наш ответ 20 метров.
Ответ: 20 метров
Замечание к заданию: ответ задания может быть записан числом от 17 до 21 метра, так как подход к сравнению размеров у каждого ученика может быть разный, в том числе кто-то использует линейку. Поэтому будет засчитано правильным ответом любое число от 17 до 21.
На рисунке изображён фрагмент карты европейской части России. Расстояние между Москвой и Тулой 180 км. Сколько приблизительно километров между Тулой и Брянском?
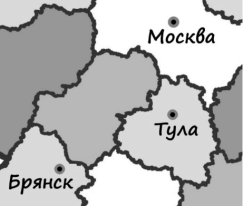
В данном задании надо оценить размеры реальных объектов, то есть двух величин – расстояний между городами. Покажем на нашем рисунке их разными цветами – известное красным отрезком, а искомое – синим отрезком
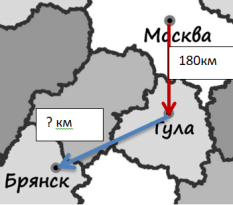
Теперь сравним наши отрезки. Красный начертим рядом с синим, откладывая с помощью линейки расстояние равное расстоянию от Москвы до Тулы.
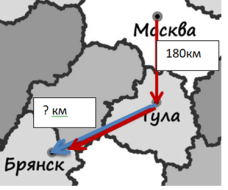
Видно, что расстояние от Москвы до Тулы короче, покажем недостающее расстояние зеленым отрезком.
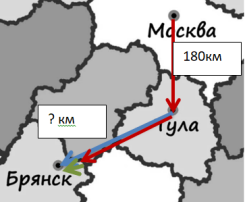
А теперь проверим, сколько таких зеленых отрезков входит в наш красный, покажем их на рисунке сверху красного:
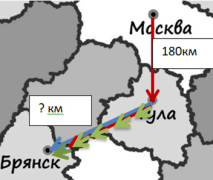
Видим, что таких зеленых отрезков вошло в наш красный четыре. Поэтому делим расстояние 180 км на 4, получаем 45 км – это длина одного зеленого отрезка. Значит, расстояние от Тулы до Брянска будет 180 + 45=225 км. Помним, что это примерное расстояние, которое зависит от выбора нашего хода решения.
Ответ: 225 км
Задание №6
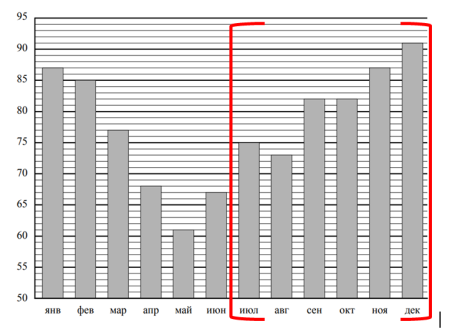
На диаграмме показана средняя влажность воздуха в Смоленске в каждом месяце. По вертикали указана влажность воздуха в процентах, по горизонтали — месяцы. В каком месяце второго полугодия средняя влажность воздуха была самой высокой?
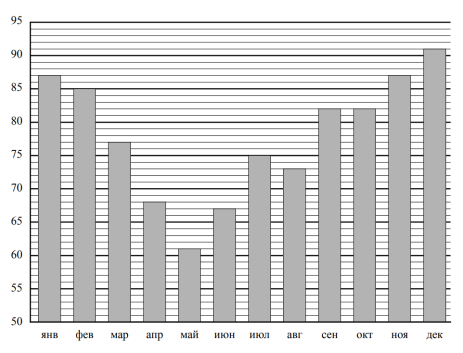
По условию задачи требуется определить, в каком месяце второго полугодия средняя влажность воздуха была самой высокой. Следовательно, надо знать, что в году два полугодия: первое с января по июнь, второе – с июля по декабрь, то есть в каждом полугодии по 6 месяцев, так как в году 12 месяцев. Значит, нам надо работать с полугодием с июля по декабрь. Покажем это полугодие на нашем рисунке с помощью скобок красного цвета.
Зная, что по вертикали указана влажность воздуха в процентах, а по горизонтали — месяцы, определяем, что наибольшая влажность воздуха была в декабре. Покажем это на нашем рисунке линией зеленого цвета.
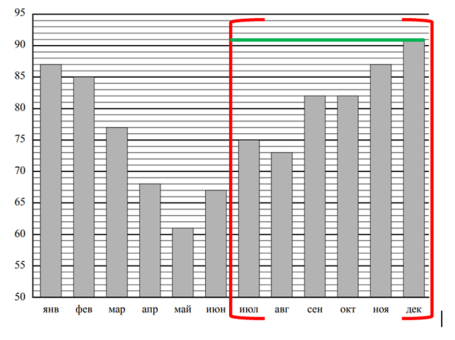
Таким образом, наш ответ — декабрь.
Ответ: декабрь
На диаграмме показано среднее количество выпавших атмосферных осадков за каждый месяц в Оренбурге в течение года. На вертикальной оси указано количество осадков (в мм), на горизонтальной — месяцы. Определите по диаграмме, сколько месяцев в Оренбурге выпадало больше 55 мм осадков за месяц.
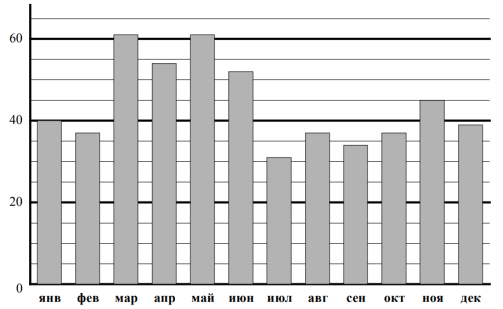
В данном задании требуется определить количество месяцев, за которые выпадало больше 55 мм осадков за месяц. Для этого нам надо определить, где на вертикальной оси данное количество. На шкале нанесены числа 20, 40 и 60, следовательно, надо определить, чему равно одно деление. На каждом отрезке, то есть от 0 до 20, от 20 до 40, от 40 до 60 есть еще по 4 отрезка. Значит, чтобы найти, чему равно одно деление на шкале, надо 20 разделить на 4, получим 5. Теперь найдем на данной вертикальной оси требуемое число – 55 мм, покажем границу 55 мм горизонтальной линией.
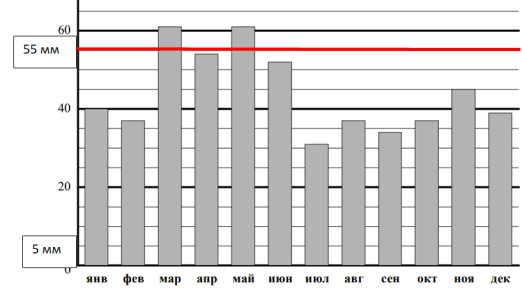
Теперь мы можем ответить на вопрос нашего задания — определить количество месяцев, за которые выпадало больше 55 мм осадков за месяц. На рисунке видно, что выше красной линии 55 мм получилось два столбика, то есть два месяца выпадало осадков выше 55 мм.
Ответ: 2
Задание №7
Найдите значение выражения: 5х−∣∣3х−14∣∣ при x = − 5
Чтобы найти значение данного выражения, надо сразу подставить значение х=− 5 в данное выражение, не раскрывая модуль.
5х−∣∣3х−14∣∣=5∙(−5)−|3∙(−5)−14|
Затем сосчитать значение выражения, стоящее под модулем и впереди него
−25−|−15−14|=−25−|−29|
И после этого раскрыть модуль, используя правило, что модуль отличного от нуля числа равен положительному числу, и найти ответ
−25−29=−54
Итак, запись общего решения выглядит следующим образом:
5х−∣∣3х−14∣∣=5∙(−5)−|3∙(−5)−14|=−25−|−15−14|=−25−|−29|=−25−29=−54
Наш ответ получился −54
Ответ: −54
Найдите значение выражения: |4х+ 9|+6x при x = − 4
Чтобы найти значение данного выражения, надо сразу подставить значение х=− 4 в данное выражение, не раскрывая модуль.
∣∣4х+9∣∣+6х=|4∙(−4)+9|+6∙(−4)
Затем сосчитать значение выражения, стоящее под модулем и после него
|−16+9|−24
И после этого раскрыть модуль, используя правило, что модуль отличного от нуля числа равен положительному числу, и найти ответ
|−7|−24=7−24=−17
Итак, запись общего решение выглядит следующим образом:
|4x+9|+6x=|4∙(−4)+9|+6∙(−4)=|−16+9|−24=|−7|−24=7−24=−17
Ответ: −17
Задание №8
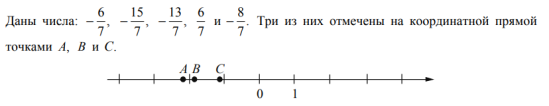
Установить соответствие между точками и числами
Точки:
А) А Б) В В) С
Числа:
1)−67 2)−157 3)−137 4)67 5)−87
В таблице для каждой точки укажите номер соответствующего числа.
| А | Б | В |
Рассмотрим рисунок и расположение данных точек на нём:
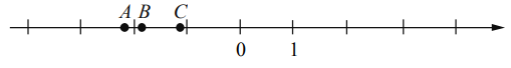
Видно, что все точки расположены левее нуля, следовательно, все числа, соответствующие им, будут отрицательными.
Нанесем на нашу координатную прямую единичные отрезки, чтобы удобнее было работать с рисунком далее:
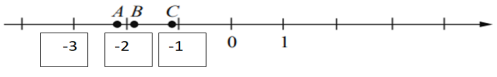
Теперь видим, что точки В и С расположены между -1 и -2, но точка С расположена ближе к -1, а точка В дальше от неё, точка А расположена на отрезке между -2 и -3, ближе к -2. То есть, если сравнить значения точек А, В и С, то значение С будет наибольшим, а значение А наименьшим. Теперь рассмотрим, какие значения (числа) нам даны по условию:
1)−67 2)−157 3)−137 4)67 5)−87
Исключим из ряда чисел число под номером 4, так как оно положительное, а их на нашей координатной прямой нет. Также исключим число под номером 1, так как оно является правильной дробью, то есть не имеет целой части, а наши данные точки располагаются, начиная с -1 целой.
Значит, осталось сравнить числа
2)−157 3)−137 5)−87
и расставить их в соответствии с буквами:
Дроби имеют одинаковые знаменатели, поэтому сравнивать будем по их отрицательным числителям −15; −13 и−8. Наибольшее, то есть ближе к нулю будет число −8 (число номер 5), значит, оно соответствует точке С, дальше будет −13 (число номер 3), оно соответствует точке В. И самое маленькое – это число −15 (число номер 2), оно соответствует точке А. Теперь запишем это в нашу таблицу
| А | Б | В |
| 2 | 3 | 5 |
Ответ: 235

Установить соответствие между точками и числами
Точки:
А) Р Б) Q В) R
Числа:
1)0,06 2)6,7 3)6,2 4)0,6 5)2,6
В таблице для каждой точки укажите номер соответствующего числа.
| А | Б | В |
Рассмотрим расположение точек на координатной прямой. Расставим на ней единичные отрезки, чтобы лучше определить координаты этих точек.

Видим, что точка Р расположена между 0 и 1, чуть за серединой этого отрезка, значит, её целая часть равна 0, а дробная — больше половины (5 десятых), то есть это точке соответствует число 0,6 (номер 4). Точка Q расположена между 2 и 3, чуть за серединой отрезка, то есть ее целая часть равна 2. У нас есть такое число под номером 5 – это 2,6. Определим координаты точки R, которая расположена между 6 и 7, а также ближе к 7. Из двух чисел – 6,7 и 6,2 это будет 6,7 (число номер 2). Теперь заполним нашу таблицу
| А | Б | В |
| 4 | 5 | 2 |
Ответ: 452
Задание №9
Вычислите: 4:1619+335∙(512−31324)
Выполним решение по порядку действий, где первое будет в скобках вычитание, затем деление, умножение и сложение. Каждое действие нужно подробно расписать в поле «РЕШЕНИЕ», чтобы получить соответствующие баллы за это задание.
Выполним вычитание:512−31324=−(31324−512)=−(31324−1024)=−3324=−318
Для выполнения данного действия мы поставили скобки и перед ними вынесли знак минус, чтобы не потерять его в ответе, так как вычитать будем из смешанного числа, которое по модулю больше. При вычитании дробей привели их к общему 24, где дробь 512=1024. Выполнили вычитание, а затем сократили дробь 324 на 3 и получили 18.
Выполним деление 4 на 1619. По правилу деления на дробь, надо от деления перейти к умножению на дробь, обратную данной, то есть на 1916
4:1619=4∙1916=1∙194=194
В процессе умножения мы сократили число 4 и знаменатель 16 на 4, откуда и получили 1 и 4.
Выполним умножение 335∙(−318)=185∙(−258)=−91∙54=−454
При умножении смешанных числе перевели их в неправильные дроби. Далее сокращали 18 и 8 на 4, получили 9 и 4. 25 и 5 сокращали на 5, получили 5 и 1. Выполнили умножение дробей, получили отрицательное число.
Выполним сложение: 194+(−454)=−264=−132=−612 или−6,5
При выполнении действия мы видим два числа с разными знаками, поэтому будем вычитать. Так как вычитаем из числа, которое больше по модулю, то ответ будет отрицательным, так как большее по модулю число – отрицательное. Также мы видим, что получилась обыкновенная неправильная сократимая дробь, поэтому сократим её на 2. Затем выделим целую часть. Ответ можно оставить в виде смешанной дроби, а можно записать в виде десятичной, вспомнив, что 12=0,5.
Ответ: −612
Задание №10
Во время диспансеризации в школе измерили рост учащихся. Оказалось, что рост каждого одиннадцатиклассника больше 160 см и меньше 195 см. Выберите верные утверждения и запишите в ответе их номера.
- Разница в росте между любыми двумя одиннадцатиклассниками этой школы или меньше, или равна 35 см.
- Рост любого одиннадцатиклассника в этой школе меньше 195 см.
- В этой школе обязательно найдётся одиннадцатиклассник ростом ровно 196 см.
- В этой школе обязательно найдётся одиннадцатиклассник ростом ровно 159 см
Чтобы решить эту простую логическую задачу, надо точно определить, что нам известно по условию: рост каждого больше 160 см и меньше 195 см. Теперь разбираем отдельно каждое утверждение и определяем – верное оно или нет.
1) Разница в росте между любыми двумя одиннадцатиклассниками этой школы или меньше, или равна 35 см. Можно сделать запись в виде неравенства, например:
160<195−160<195160<35<195
Неравенство получилось верное, значит и утверждение верное. Можно рассуждать и просто, например, если взять наибольшее и наименьшее число и найти разницу, то получится число 35. Оно может быть и меньше, например, если рост 194 наибольший, а рост 161 наименьший.
2) Рост любого одиннадцатиклассника в этой школе меньше 195 см. Утверждение верное, так как по условию задания сказано именно так (выделим жирным): рост каждого больше 160 см и меньше 195 см
3) В этой школе обязательно найдётся одиннадцатиклассник ростом ровно 196 см. Это утверждение неверное, так как сказано, что рост каждого больше 160 см и меньше 195 см.
4) В этой школе обязательно найдётся одиннадцатиклассник ростом ровно 159 см. Это утверждение также неверное, так как рост каждого больше 160 см и меньше 195 см.
Ответ: 12
Задание №11
Сумма трёх чисел равна 140. Первое число составляет 5% этой суммы. Второе число в шесть раз больше первого. Найдите третье число.
Данная задача требует решения с подробным описанием. Поэтому нужно не забыть в поле «РЕШЕНИЕ» записать каждое действие с пояснением.
Рассмотрим, что известно по условию: есть три числа, которые в сумме дают 140. Первое – 5% от суммы, от 140. Второе – в 6 раз больше первого. По порядку находим данные числа. Первое – 5% от 140, то есть вспоминаем, чтобы найти процент от числа, можно выразить его десятичной дробью (разделить на 100) и умножить на данное число, запишем это:
0,05∙140=7−первое число
Далее сказано, что второе в 6 раз больше первого, то есть надо первое число умножить на 6. Запишем действие:
7∙6=42−второе число
Теперь, зная, что сумма чисел равна 140, найдем третье число, вычитая из данной суммы первое и второе числа:
140−(7+42)=91−третье число
Ответ: третье число равно 91
На заправочной станции в январе бензин стоил 42 рубля за литр. К июлю цена на бензин выросла на 5%, а к ноябрю выросла ещё на 10%. Сколько рублей стоил литр бензина в ноябре?
Данная задача требует решения с подробным описанием. Поэтому нужно не забыть в поле «РЕШЕНИЕ» записать каждое действие с пояснением.
Рассмотрим, что известно: стоимость бензина была 42 руб, в июле выросла на 5%; в ноябре выросла на 10%. Зная это, можно найти стоимость бензина в июле и в ноябре.
Так как в июле выросла на 5%, то найдем эти 5% от исходного числа 42. Для этого переведем проценты в десятичную дробь (разделим 5 на 100) и умножим на 42. Запишем действие:
1) 0,05∙42=2,1 (руб)−на столько повысилась стоимость в июле
Теперь узнаем, сколько стал стоить бензин в июле, то есть к исходному числу 42 прибавим наши 5%:
2) 42+2,1=44,1 (руб)−стоимость в июле
Знаем, что в ноябре стоимость бензина выросла на 10% (от стоимости июля), то найдем эти 10%, выразив их десятичной дробью и умножив на новую стоимость 44,1 руб:
3)44,1∙0,1=4,41 (руб)на столько повысилась стоимость в ноябре
Ну и ответим на вопрос задачи – узнаем, сколько стал стоить бензин в ноябре. Прибавим 4,41 руб к числу 44,1:
4) 44,1+4,41=48,51(руб)стоимость бензина в ноябре
Ответ: 48,51 рублей за литр стал стоить бензин в ноябре
Задание №12
Света нарисовала фигуру на квадратном листке и сложила его (линия сгиба обозначена на рисунке). Получился отпечаток. На рисунке показана фигура и полученный отпечаток.
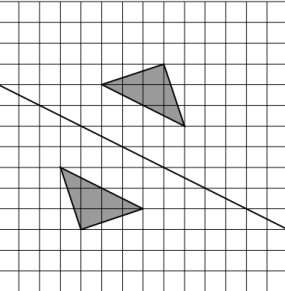
Затем на таком же листке Света нарисовала другую фигуру и сложила листок так же, как и первый листок (линия сгиба обозначена на рисунке). Нарисуйте получившийся отпечаток.
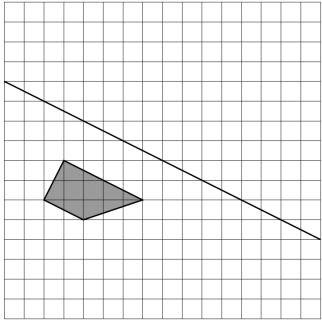
Чтобы построить другую фигуру, равную данной и находящуюся с другой стороны от прямой, надо вспомнить правило построения фигуры, симметричной данной относительно оси. То есть необходимо сначала из каждой вершины нашей фигуры, провести прямые под углом 90 градусов к данной прямой (оси симметрии). Выполним это (красным цветом показаны углы 90 градусов):
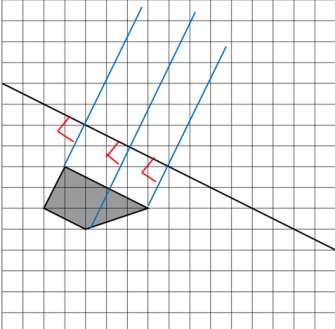
Две линии слева у нас совпали, поэтому их три, а не 4, как вершин фигуры. Теперь на наших прямых надо отложить точки на таком же расстоянии от оси, как и вершины исходной фигуры от данной оси, чтобы получить вершины новой фигуры.
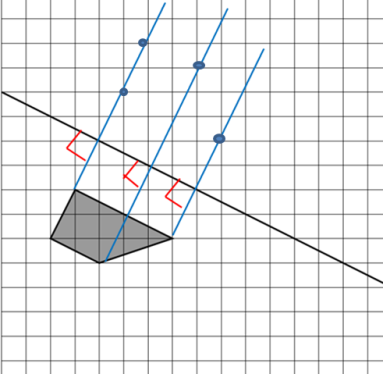
Осталось соединить наши точки отрезками и получить новую фигуру, равную данной.
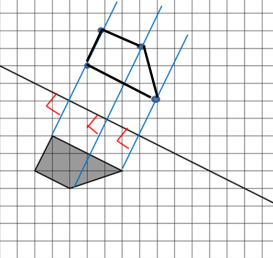
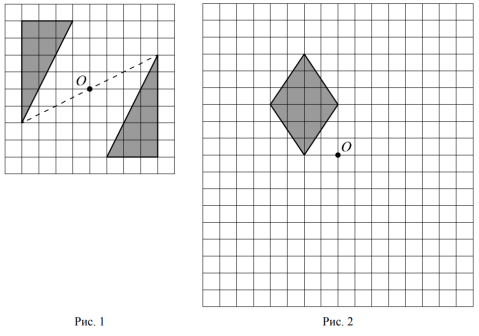
На рисунке 1 показаны фигуры, симметричные относительно точки O. На рисунке 2 показаны фигура и точка O. Нарисуйте фигуру, симметричную данной фигуре относительно точки O, на рисунке 2.
Чтобы построить другую фигуру, равную данной, надо вспомнить правило построения фигуры, симметричной данной относительно заданной точки (центра симметрии). Для начала из каждой вершины фигуры нужно провести лучи через заданную точку О.
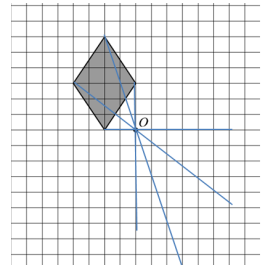
Теперь от точки О откладываем отрезки, равные каждому из отрезков от данных вершин до точки О и отмечаем их точками.
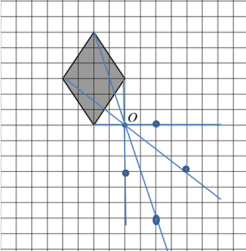
Соединим данные точки и получим фигуру, симметричную данной.
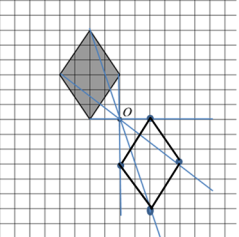
Задание №13
Вася и Маша не умеют сокращать дроби. Они делают это неправильно. Вася думает, что при сокращении дроби нужно от числителя отнять 3, а от знаменателя отнять 2. Вася делает так: 64=6−34−2=32
Маша считает, что при сокращении дроби нужно от числителя отнять 2, а от знаменателя отнять 1. Маша делает так:42=4−22−1=21
Вася и Маша (не обязательно по очереди) тридцать раз «сократили» по своим правилам дробь 20202021 и получили дробь со знаменателем 1989. Найдите числитель получившейся дроби.
Данная задача требует решения с подробным описанием. Поэтому нужно не забыть в поле «РЕШЕНИЕ» записать все рассуждения к задаче.
Запишем, какая дробь была, и какая должна получиться, как сказано в условии: 20202021=?1989. Итак, вместо вопросительного знака у нас должно получиться число.
Теперь, если посмотреть на дроби, которые получались у Васи и Маши после их неправильного сокращения, то можно заметить, что разница между числителем и знаменателем равна 1.
После каждого «сокращения» данной дроби разность между знаменателем и числителем увеличивается на 1. Значит, после тридцати преобразований эта разность равна 2021-2020+30=31, поэтому числитель равен 1989-31=1958.
Ответ: числитель дроби равен 1958
В погребе хранилось несколько головок сыра. Ночью пришли мышки и съели 4 головки сыра, причём все съели поровну. Следующей ночью пришли не все мышки, а только 9, и доели оставшийся сыр, но каждая мышка съела в два раза меньше сыра, чем накануне. Сколько головок сыра хранилось в погребе? Запишите решение и ответ.
Данная задача требует решения с подробным описанием. Поэтому нужно не забыть в поле «РЕШЕНИЕ» записать все рассуждения к задаче.
Рассмотрим условие и запишем необходимые рассуждения.
В погребе хранилось несколько головок сыра. Ночью пришли мышки и съели 4 головки сыра, причём все съели поровну. То есть мышей было неизвестно, например, обозначим их количество за «х». Тогда каждая съела 4х головок сыра.
Следующей ночью пришли не все мышки, а только 9. Они доели оставшийся сыр, но каждая мышка съела в два раза меньше сыра, чем накануне. Значит, можно обозначить за «у» оставшийся сыр, тогда у9∙2 съела каждая из них.
Составим равенство 4х=2∙у9, упростим его по свойству пропорции (произведение крайних членов равно произведению средних членов), получаем 4х=2у9; 36=2х∙у; разделим обе части на 2, получим 18=х∙у.
Поскольку сказано, что во вторую ночь было 9 мышей, а это больше, чем в первую, значит, всего мышей было больше 9. То есть х>9 и х – натуральное число, так как обозначает количество мышей. Тогда х=18, значит, в равенство 18=х∙у подставим 18 вместо х и получим, что у=1, то есть 1 головка сыра оставалась на второй день. Следовательно, всего их было первоначально 5 (не забываем, что в первый день они съели 4 головки сыра).
Ответ: 5