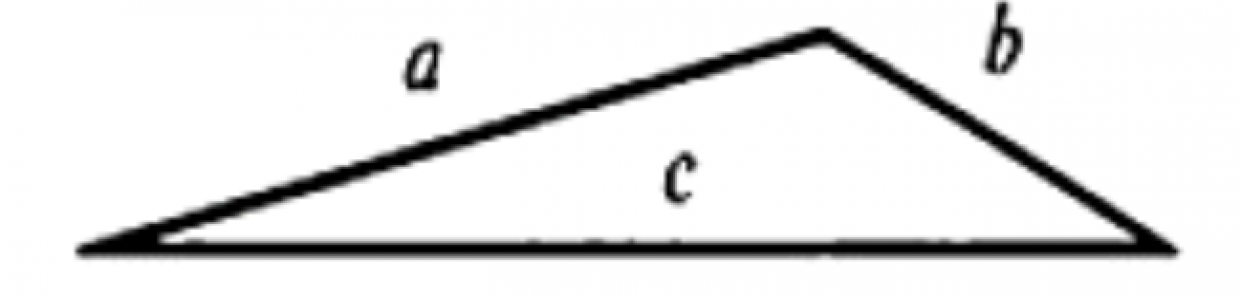
На данном рисунке показан произвольный треугольник, стороны которого обозначены для удобства буквами а, b, c. Так, в соответствии с неравенством треугольника:
- а<c+b
- b<a+c
- c<a+b
Неравенство треугольника используется при решении задач на построение или на определение существования треугольника. Рассмотрим это на конкретных примерах:
Можно ли построить треугольник со сторонами 12, 18 и 23 см?
Для ответа на вопрос данной задачи нужно проверить каждую сторону на верность неравенства: 12<18+23 (верно); 18<12+23 (верно); 23<12+18 (верно). Если все три равенства верны, значит, треугольник со сторонами 12, 18 и 23 см можно построить.
Существует ли треугольник со сторонами 19, 31 и 11 см?
Для ответа на вопрос данной задачи нужно также проверить каждую сторону на верность неравенства: 19<31+11 (верно); 31<19+11 (не верно); 11<19+31 (не верно). Так как не все три равенства верны, значит, треугольник со сторонами 19, 21 и 11 см не существует.
Сделаем вывод, что, если хотя бы одно неравенство не является верным, то не выполняется неравенство треугольника и поэтому треугольника с указанными сторонами не существует, следовательно, и построить его тоже нельзя.
Почему в задаче где нужно понять можно ли построить треугольник со сторонами 19,21 и 11 см? Не верно!? Если правило гласит так : каждая сторона треугольника меньше суммы двух других сторон. В объяснение задачи вы пишите, что 11<21+19 и считаете это неверным, если 11<40. Не считаете это странным?
Спасибо, Виктория, поправили!