Прямая
Теперь представим, что проведенная на плоскости линия будет увеличиваться вместе с ней. Получается, что прямая тоже бесконечна. На бумаге мы изображаем только часть прямой. Прямую обозначают одной строчной буквой латинского алфавита. Например, b (рис.1). Так как через две точки на плоскости проходит одна прямая, то прямую можно обозначить двумя латинскими заглавными буквами, которыми обозначают точки на этой прямой (рис. 2), например, АС или СА.
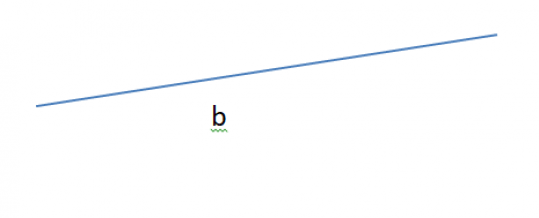
Рисунок №1. Обозначение прямой одной строчной буквой. Прямая b.
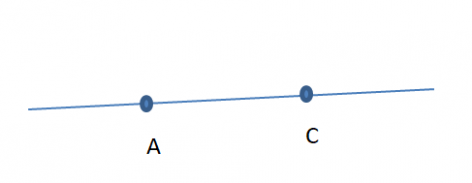
Рисунок 2. Обозначение прямой двумя латинскими буквами. Прямая AB.
Луч
Если на прямой АС поставить еще одну букву, например, О, то получим, что точка О делит прямую на две части, каждая из которых называется лучом (рис.3).
Итак, луч – имеет начало, но не имеет конца. Называть лучи на рисунке 3 можно ОА или ОС (на первом месте ставится буква, которая обозначает начало луча).
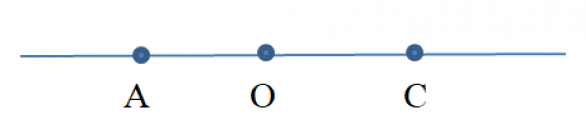
Рисунок №3. Лучи OA и OC.
Рисунок 4
Перпендикуляр и наклонная
К любому отрезку можно провести перпендикулярную прямую. Вспомним, что перпендикулярной прямой называется прямая, проведенная под углом 90 градусов.
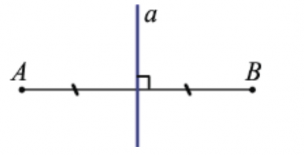
Серединный перпендикуляр к отрезку AB.
На данном рисунке мы видим, что отрезок разделен на две равные части (показаны штрихами), а через середину проведена прямая а под углом 900 к данному отрезку АВ. Следовательно, прямая а – серединный перпендикуляр к отрезку АВ.
Свойство серединного перпендикуляра
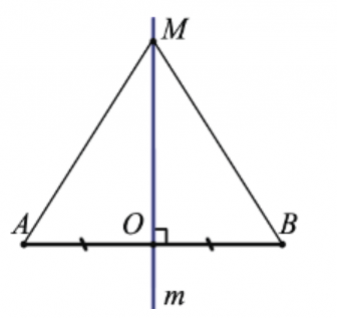
На данном рисунке через середину О отрезка АВ проходит прямая m, которая является серединным перпендикуляром. На этой прямой взята некоторая точка М. По свойству серединного перпендикуляра к отрезку, расстояния от точки М до концов отрезка АВ будут равны, то есть АМ=МВ.
Если прямая, проведённая через данную точку, пересекает прямую (отрезок), но не перпендикулярна к ней, то ее называют наклонной. Наклонная всегда больше перпендикуляра.
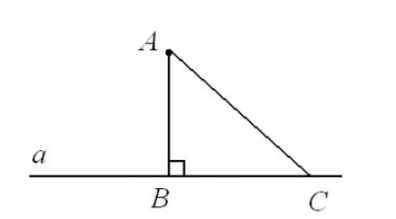
На данном рисунке АВ – перпендикуляр, а АС – наклонная к прямой а. Видим, что действительно АС>ВС. Точку В называют основанием перпендикуляра, а точку С – основанием наклонной.