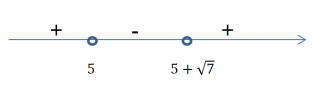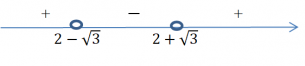Квадратные неравенства с одной переменной | теория по математике 🎲 неравенства

Определение

Неравенство вида ax²+bx+c>0 или ax²+bx+c<0, где х – переменная, a, b и c некоторые числа называют неравенством второй степени с одной переменной (или квадратными неравенствами). Также в неравенствах могут встречаться знаки ≤ или ≥.

Для решения неравенства находят промежутки, в которых функция у=ax²+bx+c принимает положительные или отрицательные значения, это зависит от знака неравенства, данного в стандартном виде. Для этого достаточно определить, в каком направлении расположены ветви параболы у=ax²+bx+c, а также найти нули данной функции, относительно которых и определяются промежутки.

Вспомним, что ветви параболы направлены вверх при а>0, ветви направлены вниз при а<0. Для нахождения нулей функции необходимо решить обычное квадратное уравнение, то есть найти дискриминант и корни квадратного трехчлена ax²+bx+c.

Алгоритм решения неравенства второй степени с одной переменной

Порядок действий

Находим дискриминант квадратного трехчлена ax²+bx+c и выясняем, имеет ли уравнение корни.
- Если квадратный трехчлен имеет два корня (D>0), то на оси х отмечаем две точки (выколотые или приколотые, в зависимости от знака исходного неравенства) и проводим через них параболу ветвями вверх/вниз (зависит от условия).
- Если квадратный трехчлен имеет два одинаковых корня (D=0), то отмечаем одну точку на оси х – вершину параболы, проводим из этой точки её ветви.
- Если квадратный трехчлен не имеет корней (D<0), то изображаем параболу схематически в одной из полуплоскостей, это зависит от направления ветвей (а>0 – расположена в верхней полуплоскости ветвями вверх; а<0 – расположена в нижней полуплоскости ветвями вниз).
находим на оси х промежутки, для которых точки параболы расположены выше оси х (если условие дано для чисел больших нуля) или ниже оси х (если условие дано для чисел меньших нуля).

Первый случай. D>0, a>0.

Решить неравенство:

х²+2х–48<0

Неравенство дано в стандартном виде. Находим дискриминант квадратного трехчлена х²+2х–48:

D=b²–4ac=2²-=4+192=196>0

Значит, квадратный трехчлен имеет два корня, находим их по формуле:

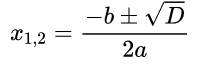
Это будут числа –8 и 6. Нам надо на оси х отметить две выколотые точки и построить параболу ветвями вверх, так как число а=1, то есть а>0. Теперь для ответа определяем промежуток отрицательных чисел, так как в условии неравенства стоит знак «меньше».

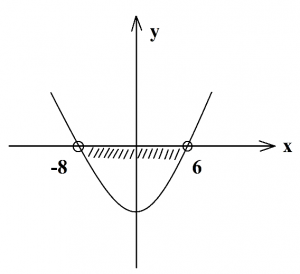Это будут все числа, расположенные ниже оси х (на рисунке промежуток заштрихован), в ответ запишем промежуток чисел (–8;6).

Второй случай. D>0, a<0.

Решить неравенство:

–х²+2х+15<0

Находим дискриминант, он равен 64, значит, квадратный трехчлен имеет два корня. Находим по известной формуле эти корни, получим –3 и 5. Отмечаем на оси х эти две выколотые точки и проводим параболу ветвями вниз, так как a<0 по условию. Теперь для ответа определяем промежуток отрицательных чисел, так как в условии неравенства стоит знак «меньше».

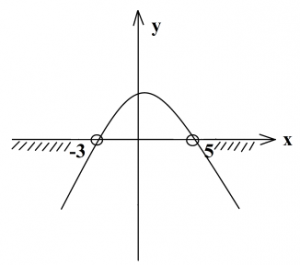
Это будут все числа, расположенные ниже оси х (промежутки показаны штриховкой), в ответ запишем промежутки чисел (-∞;-3)∪(5:+∞).

Третий случай. D=0, a<0.

Решить неравенство:

4х²–12х+9>0

Находим дискриминант, он равен нулю. Значит, имеем корень, который равен 1,5. Отмечаем на оси х выколотую точку, это будет вершина параболы, проводим параболу ветвями вверх, так как а=4. Теперь определяем промежуток положительных чисел, это все числа, которые находятся выше оси х (показаны штриховкой).

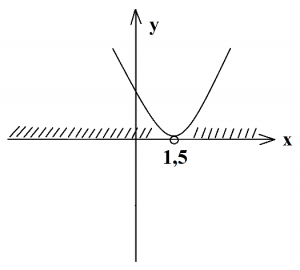
То есть, это числа от минус бесконечности до 1,5 и от 1,5 до плюс бесконечности, так как точка 1,5 выколотая, а значит, она не входит в данный промежуток чисел. Запишем ответ: (-∞;-1,5)∪(1,5:+∞). Также данный ответ можно записать короче: х≠1,5.

Четвертый случай. D<0, a>0.

Решить неравенство:

5х²+6х+9<0

Находим дискриминант, он равен –144, значит, квадратный трехчлен не имеет корней. В координатной плоскости покажем параболу, которая не пересекает ось х, то есть расположена в верхней полуплоскости ветвями вверх, так как а=5. Теперь для нахождения ответа определяем промежуток отрицательных чисел: так как парабола находится в верхней полуплоскости, а нужен промежуток отрицательных чисел (показан штриховкой), то данное неравенство не имеет решений.

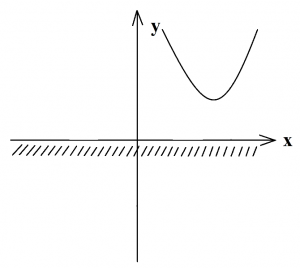
Записываем ответ: нет решений.

Пятый случай. D<0, a<0.

Решить неравенство:

–10х²+3х–2≤0

Находим дискриминант, он равен отрицательному числу (–71), значит, корней нет. В координатной плоскости покажем параболу, которая не пересекает ось х, то есть, расположена в нижней полуплоскости ветвями вниз, так как а=–10. Теперь для нахождения ответа определяем промежуток отрицательных чисел: так как парабола находится в нижней полуплоскости, а нам нужен промежуток отрицательных чисел (показан штриховкой), то данное неравенство имеет множество решений (искомый промежуток совпал с расположением параболы в нижней полуплоскости).

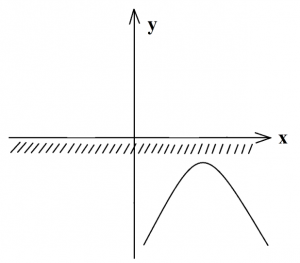
C:UsersO2Desktop4.png

Записываем ответ: множество решений. Также ответ можно записать в виде промежутка (-∞;+∞) или записать так: х – любое число.

Текст: Базанов Даниил, 5.8k 👀

Задание OM2005

Решить неравенство(

{х - 5)}^{2} < \sqrt{7} (х - 5)

Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:

${(х - 5)}^{2} - \sqrt{7} (х - 5) < 0$

Теперь вынесем за скобки общий множитель (х-5), получим:

$(х - 5) (х - 5 - \sqrt{7}) < 0$

Найдем нули функции, приравнивая каждый множитель к нулю:

$х - 5 = 0$ , откуда х=5

$х - 5 - \sqrt{7} = 0,$

откуда:

$х = 5 + \sqrt{7}$

Отметим эти числа на числовом луче и найдем интервал отрицательных чисел:

Итак, видно, что необходимый интервал от 5 до $(5 + \sqrt{7})$

Ответ: $(5; 5 + \sqrt{7}$ $)$

Ответ: см. решение

pазбирался: Базанов Даниил | обсудить разбор

Задание OM2003

Решить неравенство

\frac{- 11}{{(х - 2)}^{2} - 3} \geq 0

Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:

(х – 2)² – 3 $< 0$

У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:

х² – 4х+4 – 3 $< 0$

х² – 4х+1 $< 0$

Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел ( $< 0$ )

Для этого найдем нули функции, решая с помощью дискриминанта:

Д=(-4)² — 4 $∙ 1 ∙ 1$ =16-4=12

$х_{1} = \frac{4 - \sqrt{12}}{2} = \frac{2 (2 - \sqrt{3)}}{2} = 2 - \sqrt{3}$

Знаем, что х₂ будет отличаться только знаком, получим, что $х_{2} = 2 + \sqrt{3}$

Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки $(2 - \sqrt{3)}$ до точки $(2 + \sqrt{3)}$ .

Ответ: $(2 - \sqrt{3}$ ; $2 + \sqrt{3})$

pазбирался: Базанов Даниил | обсудить разбор

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Алгоритм решения неравенства второй степени с одной переменной

Первый случай. D>0, a>0.

Второй случай. D>0, a<0.

Третий случай. D=0, a<0.

Четвертый случай. D<0, a>0.

Пятый случай. D<0, a<0.

Задание OM2005

Задание OM2003

Вся теория

Добавить комментарий Отменить ответ