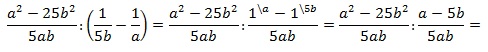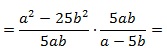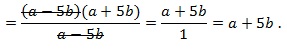Примеры алгебраических дробей:
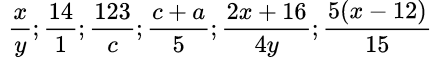
Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.
Сокращение алгебраической дроби
Пример №1. Сократим дробь:
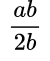
В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:
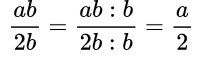
Промежуточные действия можно не записывать, а выполнять устно.
Пример №2. Сократим дробь:
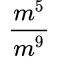
Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m5:
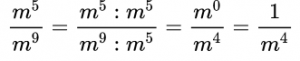
Пример №3. Сократим дробь:
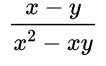
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).
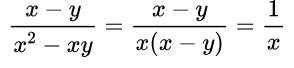
Пример №4. Сократим дробь:
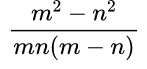
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m2– n2=(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).
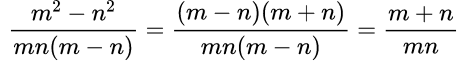
Сложение и вычитание алгебраических дробей с одинаковым знаменателем
Пример №5. Выполним сложение дробей:
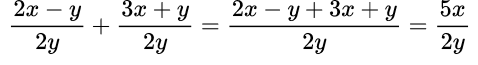
Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.
Пример №6. Выполним вычитание дробей:
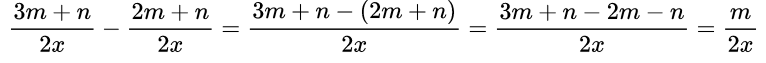
В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.
Сложение и вычитание алгебраических дробей с разными знаменателями
Пример №7. Выполнить сложение дробей:
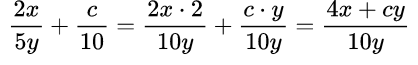
Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.
Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.
Пример №8. Выполнить вычитание дробей:
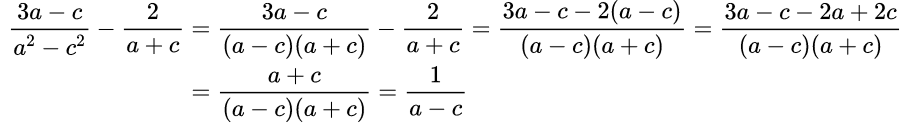
Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а2 – с2=(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).
Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).
Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).
Умножение алгебраических дробей
Пример №9. Выполнить умножение дробей:
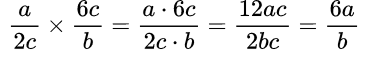
Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.
Пример №10. Выполнить умножение дробей:
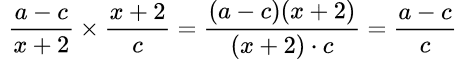
Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.
Деление алгебраических дробей
Пример №11. Выполнить деление дробей:
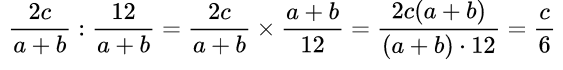
Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.