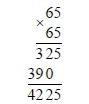При переводе обыкновенной дроби в десятичную можно получить конечную периодическую или бесконечную десятичные дроби (кроме простой десятичной, разумеется).
Пример №1. ¾ — делим 3 на 4 и получаем 0,75.
Пример №2. 31/50 делим 31 на 50 и получаем 0,62.
Пример №3. 3/25 делим 3 на 25 и получаем 0,12.
Пример №4. 7/12 При делении 7 на 12 получается 0,5833333…, где постоянно повторяется цифра 3, запись делают следующим образом: 0,58(3); читается эта дробь следующим образом: нуль целых пятьдесят восемь сотых и три в периоде.
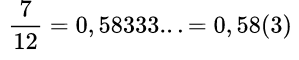
Пример №5. 1/11 При делении 1 на 11 получается 0,090909… и так до бесконечности повторяются цифры 0 и 9. Данную дробь записывают в виде 0,(09) и читают как нуль целых и нуль десять в периоде.
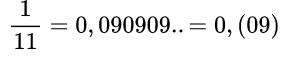
Пример №6. √15=3,8729833….
Пример №7. π = 3,1415926535…