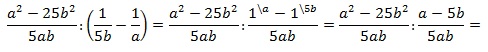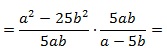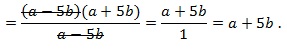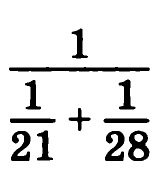Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
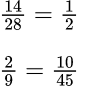
Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.
- Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
- Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
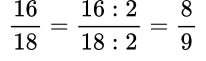
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
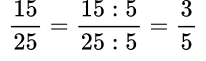
Пример №4.
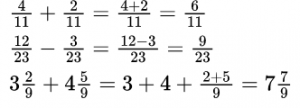
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
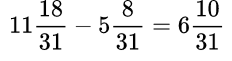
Вычитание обыкновенной дроби из целого числа
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
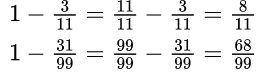
Пример №6.
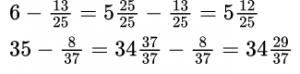
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7.
1. Нужно разложить на простые множители каждое число:
12=2×2×3
15=3×5
2. Затем найти одинаковые множители (подчеркиваем):
12=2×2×3
15=3×5
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Пример №8.
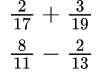
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
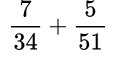
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Пример №10.
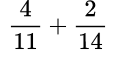
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
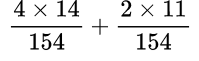
Выполняем умножение в числителе:
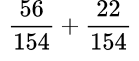
Выполняем сложение дробей с одинаковыми знаменателями:
![]()
Умножение обыкновенных дробей
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
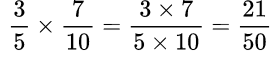
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
![]()
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
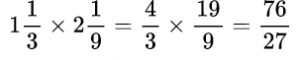
Деление обыкновенных дробей
Пример №14. Делимое умножаем на число, обратное делителю.
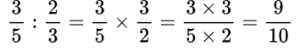
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.
![]()
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
![]()