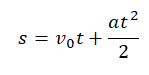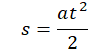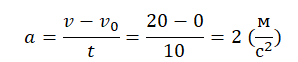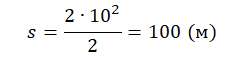Перемещение и путь при равноускоренном прямолинейном движении | теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀= 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁ оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁= 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2.Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Текст: Алиса Никитина, 32.9k 👀

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t $-$ 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

$x (t) = x_{0} + v_{0} t + \frac{a t^{2}}{2}$

Теперь мы можем выделить кинематические характеристики движения тела:

• x₀ = 10 (м).

• v₀ = 5 (м/с).

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

$s = v_{0} t + \frac{a t^{2}}{2}$

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

$x (t) = v_{0} t + \frac{a t^{2}}{2} = 5 t - 3 t^{2}$

Кинетическая энергия тела определяется формулой:

$E_{k} = \frac{m v^{2}}{2}$

Скорость при прямолинейном равноускоренном движении равна:

$v = v_{0} + a t = 5 - 6 t$

Поэтому кинетическая энергия тела равна:

$E_{k} = \frac{m {(5 - 6 t)}^{2}}{2} = \frac{0, 2}{2} {(5 - 6 t)}^{2} = 0, 1 {(5 - 6 t)}^{2}$

Следовательно, правильная последовательность цифр в ответе будет: 34.

.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17957

За 10 секунд скорость автомобиля, движущегося равноускоренно по прямой дороге, увеличилась от 0 до 20 м/с. Пройденный автомобилем путь равен…

Алгоритм решения

Записать исходные данные.
Записать формулу для определения пути при равноускоренном прямолинейном движении.
Определить недостающие исходные данные.
Найти искомую величину.

Решение

Запишем исходные данные:

Начальная скорость v₀ = 0 м/с.
Конечная скорость v = 20 м/с.
Время изменения скорости t = 10 с.

Формула для вычисления пути при равноускоренном прямолинейном движении:

Так как начальная скорость равна нулю, формула принимает вид:

Нам неизвестно ускорение, но его можно вычислить по формуле:

Вычисляем путь:

Ответ: 100

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18831

На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от

t_{1} = 20

с до

t_{2} = 50

с.

Алгоритм решения

Охарактеризовать движение тела на различных участках графика.
Выделить участки движения, над которыми нужно работать по условию задачи.
Записать исходные данные.
Записать формулу определения искомой величины.
Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

Исходные данные:

Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s = s₁ + s₂

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁ и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁ и s₂, а затем сложим их:

s₁ + s₂ = 100 + 100 = 200 (м)

Ответ: 200

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Перемещение при разгоне и торможении тела

Этап торможения

Этап разгона

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Проекция и график перемещения

График пути

Задание EF18553

Задание EF18774

Задание EF17957

Задание EF18831

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ