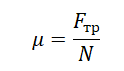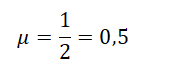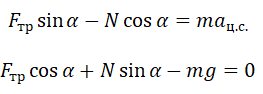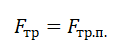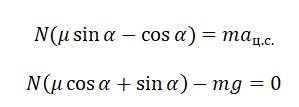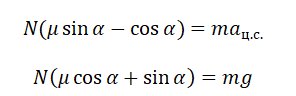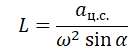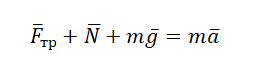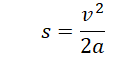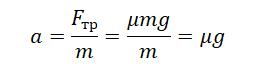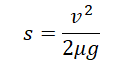Сила трения | теория по физике 🧲 динамика

Определения

Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.

Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как F_тр. Единица измерения — Н (Ньютон).

Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.

Виды сухого трения:

трение скольжения;
трение качения;
трение покоя.

Трение скольжения

Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: F_тр↑↓v.

Сила трения скольжения определяется формулой:

μ — коэффициент трения, N — сила реакции опоры, F_давл. — сила нормального давления

Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.

Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.

Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.

Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.

Полезные факты

Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
Сила трения скольжения не зависит от площади соприкосновения тел.
Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.

Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?

Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:

Трение покоя

Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).

Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:

0 < F_тр.пок. < F_{тр. ск.}

Способы определения вида силы трения, возникающей между телами, и ее модуля:

Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < F_{тр. ск.}, F_тр.пок.= F.
Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ F_{тр. ск.}, F_тр.= F_тр.ск.

Графически это можно изобразить так:

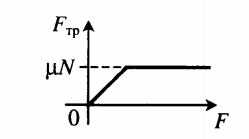
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?

Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.

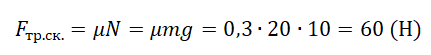
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:

F_тр.пок. = F = 36 (Н).

Описание движения тел с учетом сил трения

Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.

Движение тела по горизонтальной плоскости

Равноускоренное движение по горизонтали, сила тяги параллельная плоскости
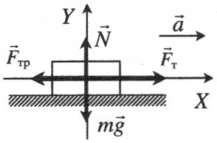	Второй закон Ньютона в векторной форме: mg + N + F_т + F_тр = ma Проекция на ось ОХ: F_т – F_тр = ma Проекция на ось ОУ: N – mg = 0
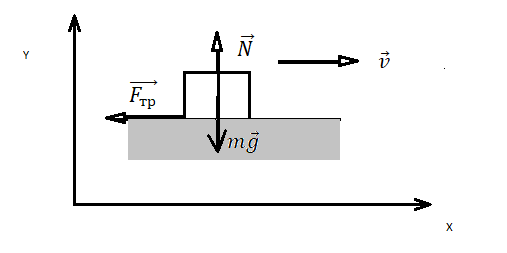
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости
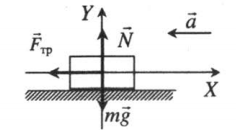	Второй закон Ньютона в векторной форме: mg + N + F_т + F_тр = ma Проекция на ось ОХ: – F_тр = –ma Проекция на ось ОУ: N – mg = 0
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх)
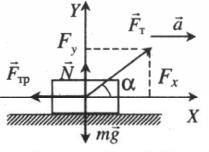	Второй закон Ньютона в векторной форме: mg + N + F_т + F_тр = ma Проекция на ось ОХ: F_тcosα – F_тр = ma Проекция на ось ОУ: F_тsinα + N – mg = 0
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз)
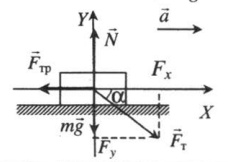	Второй закон Ньютона в векторной форме: mg + N + F_т + F_тр = ma Проекция на ось ОХ: F_тcosα – F_тр = ma Проекция на ось ОУ: N – F_тsinα – mg = 0

Внимание! В случаях, когда сила тяги F_т направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.

Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?

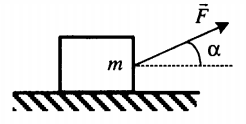
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:

F_тр = μN

Проекция сил на ось ОУ выглядит так:

N – F_тsinα – mg = 0

Отсюда силы реакции опоры равна:

N = F_тsinα + mg

Подставим ее в формулу для вычисления силы трения и получим:

F_тр = μN = μ (F_тsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)

Движение тела по вертикальной плоскости

Тело прижали к вертикальной плоскости и удерживают
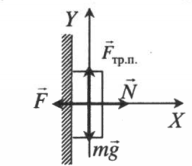	Второй закон Ньютона в векторной форме: mg + N + F_т + F_тр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: F_т.п. – mg = 0
Тело поднимается под действием силы тяги, направленной под углом к вертикали
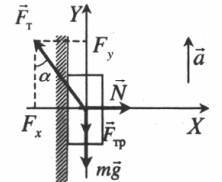	Второй закон Ньютона в векторной форме: mg + N + F_т + F_тр = ma Проекция на ось ОХ: N – F_тsinα = 0 Проекция на ось ОУ: F_тcosα – F_тр – mg = 0

Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.

Проекция на ось ОХ:

N – F = 0

Отсюда следует, что сила должна быть равна силе реакции опоры.

Проекция на ось ОУ:

F_т.п. – mg = 0

Перепишем, выразив силу трения через силу реакции опоры:

μN – mg = 0

Отсюда выразим силу реакции опоры:

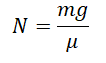
Следовательно:

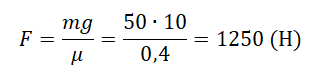
Движение тела по наклонной плоскости

Движение вниз без трения
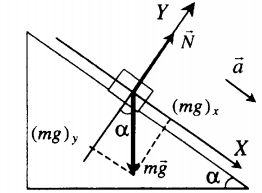	Второй закон Ньютона в векторной форме:
	mg + N = ma
	Проекция на ось ОХ:
	mg sinα = ma
	Проекция на ось ОУ:
	N – mg cosα = 0
Тело покоится на наклонной плоскости
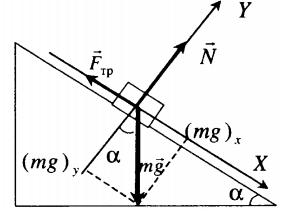	Второй закон Ньютона в векторной форме:
	mg + N + F_тр = ma
	Проекция на ось ОХ:
	mg sinα – F_тр.п.= 0
	Проекция на ось ОУ:
	N – mg cosα = 0
Тело удерживают на наклонной плоскости
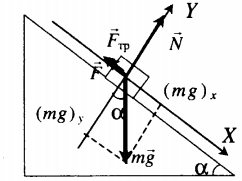	Второй закон Ньютона в векторной форме:
	mg + N + F + F_тр = ma
	Проекция на ось ОХ:
	F + F_тр. – mg sinα = ma
	Проекция на ось ОУ:
	N – mg cosα = 0
Равноускоренное движение вверх с учетом силы трения
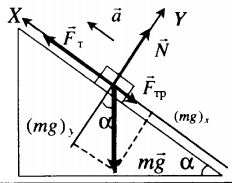	Второй закон Ньютона в векторной форме:
	mg + N + F_т + F_тр = ma
	Проекция на ось ОХ:
	F_т – mg sinα – F_тр.= ma
	Проекция на ось ОУ:
	N – mg cosα = 0
Равномерное движение вверх с учетом силы трения
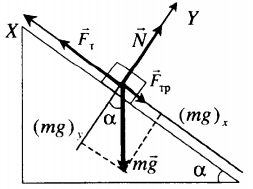	Второй закон Ньютона в векторной форме:
	mg + N + F + F_тр = ma
	Проекция на ось ОХ:
	F_т – mg sinα – F_тр.= 0
	Проекция на ось ОУ:
	N – mg cosα = 0

Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.

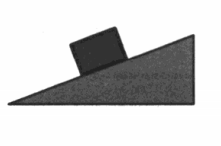
Переведем массу в килограммы: 200 г = 0,2 кг.

Проекция сил, действующих на тело, на ось ОХ:

mg sinα – F_тр.п. = 0

Отсюда сила трения равна:

F_тр.п. = mg sin α

Подставляем известные данные и вычисляем:

F_тр.п. = 0,2∙10∙sin30^o = 2∙0,5 = 1 (Н)

Полезная информация

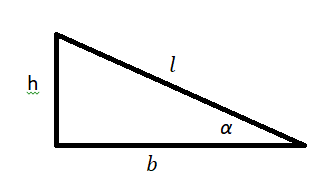
Косинус угла наклона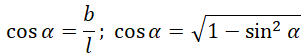
Синус угла наклона (уклон)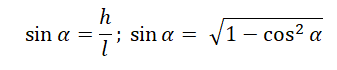
Тангенс угла наклона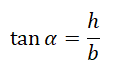

Текст: Алиса Никитина, 19.1k 👀

Задание EF18204

При исследовании зависимости силы трения скольжения F_тр от силы нормального давления F_д были получены следующие данные:

F_тр, Н	1,0	2,0	3,0	4,0
F_д, Н	2,0	4,0	6,0	8,0

Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:

а) 0,2 б) 2 в) 0,5 г) 5

Алгоритм решения

1.Записать формулу, связывающую силу трения с силой нормального давления.

2.Выразить из нее коэффициент трения.

3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).

4.Вычислить коэффициент трения на основании табличных данных.

Решение

Силу трения и силу нормального давления связывает формула:

F_тр = μN

Отсюда коэффициент трения равен:

Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17513

Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.

Алгоритм решения

1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.

2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.

3.Записать второй закон Ньютона в виде проекций на оси.

4.Через систему уравнений вывести искомую величину.

Решение

Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.

Второй закон Ньютона в векторном виде выглядит следующим образом:

Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:

Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:

Максимальное значение силы трения равно:

Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:

Запишем систему уравнение в следующем виде:

Поделим первое уравнение на второе и получим:

Сделаем сокращения и получим:

Отсюда центростремительное ускорение равно:

Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:

Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:

Отсюда центростремительное ускорение равно:

Выразим искомую величину L:

Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:

Поделим числитель на синус угла α, чтобы упростить выражение, и получим:

.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18051

Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.

5.Записать формулу для нахождения силы трения скольжения.

6.Записать формулу для расчета перемещения при движении с постоянным ускорением.

7.Использовать второй закон Ньютона для определения тормозного пути.

Решение

Из условий задачи нам известны следующие величины:

• Начальная скорость грузовика (до начала торможения) v₀ = v.

• Масса грузовика m.

• Коэффициент трения между колесами и дорогой μ.

Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:

Запишем второй закон Ньютона в векторной форме:

Запишем второй закон Ньютона в проекциях на оси:

F_тр = ma

N – mg = 0

Известно, что сила трения скольжения определяется формулой:

F_тр = μN = μmg

Значит, в первую ячейку таблицы мы должны поставить «1».

Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):

Выразим ускорение через проекцию сил на ось ОХ:

Подставим найденное ускорение в формулу тормозного пути и получим:

Следовательно, во вторую ячейку таблицы мы должны поставить «4».

Полный ответ: «14».

.

Ответ: 14

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Трение скольжения

Трение покоя

Описание движения тел с учетом сил трения

Движение тела по горизонтальной плоскости

Равноускоренное движение по горизонтали, сила тяги параллельная плоскости

Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости

Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх)

Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз)

Движение тела по вертикальной плоскости

Тело прижали к вертикальной плоскости и удерживают

Тело поднимается под действием силы тяги, направленной под углом к вертикали

Движение тела по наклонной плоскости

Движение вниз без трения

Тело покоится на наклонной плоскости

Тело удерживают на наклонной плоскости

Равноускоренное движение вверх с учетом силы трения

Равномерное движение вверх с учетом силы трения

Задание EF18204

Задание EF17513

Задание EF18051

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ