В запаянной с одного конца трубке находится влажный воздух, отделённый от атмосферы столбиком ртути длиной l = 76 мм. Когда трубка лежит горизонтально, относительная влажность воздуха ϕ1 в ней равна 80%. Какой станет относительная влажность этого воздуха ϕ2 , если трубку поставить вертикально, открытым концом вниз? Атмосферное давление равно 760 мм рт. ст. Температуру считать постоянной.
Алгоритм решения:
1.Записать исходные данные. При необходимости перевести единицы измерения в СИ.
2.Сделать поясняющий рисунок.
3.Определить относительную влажность воздуха в случаях 1 и 2.
4.Определить давление влажного воздуха в случаях 1 и 2.
5.Определить тип изопроцесса, записать и применить к нему соответствующий закон.
6.Записать и применить уравнение состояния идеального газа.
7.Привести необходимые преобразования с записанными формулами, чтобы вывести искомую величину.
8.Подставить известные величины и произвести вычисления.
Решение:
Запишем исходные данные:
• Длина столбика ртути: l = 76 мм.
• Относительная влажность воздуха в горизонтально расположенной трубке: ϕ1 = 80%.
• Атмосферное давление: p0 = 760 мм. рт. ст.
• Температура в случаях 1 и 2 (когда трубка расположена горизонтально и вертикально): T1 = T2 = const.
Из исходных данных видно, что системе СИ не соответствуют длина столбика ртути и атмосферное давление. Их необходимо перевести в метры (м) и Паскали (Па) соответственно. Однако мы можем этого не делать, если условимся, что при вычислениях будем использовать соразмерные величины. То есть, при расчете длин будем пользоваться миллиметрами (мм), а при расчете давлений — миллиметры ртутного столба (мм. рт. ст.). В рамках решения конкретной задачи это будет нам удобнее.
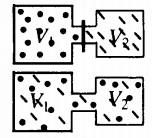
Сделаем поясняющие рисунки для случаев 1 и 2:
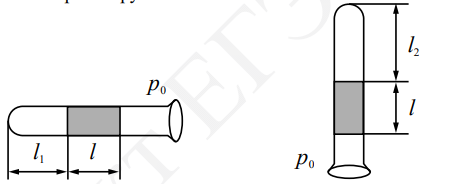
За l1 и l2 мы взяли длину столбика влажного воздуха в 1 и 2 случаях соответственно. За p0 берем атмосферное давление. А l — длина столбика ртути, которая остается для обоих случаев неизменной.
Относительная влажность воздуха определяется формулой:
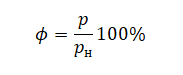
p — это давление водяных паров, а pн — давление насыщенных водяных паров при той же температуре. С помощью этой формулы запишем относительные влажности воздуха в трубке для случаев 1 и 2 соответственно:
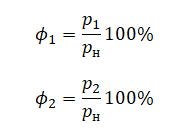
Выразим относительную влажность воздуха 2:
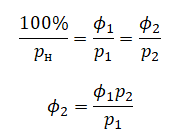
Теперь определим общее давление влажного воздуха в случаях 1 и 2. Когда трубка расположена горизонтально, ртуть, которая находится с открытого конца трубки, никак не давит на влажный воздух. Поэтому давление, оказываемое влажным воздухом, приходит в равновесие только с атмосферным давлением. Следовательно, давление влажного воздуха в 1 случае равно атмосферному давлению:
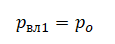
Когда трубка принимает вертикальное положение, и столбик ртути оказывается ниже столбика с влажным воздухом, влажный воздух приходит в равновесие с атмосферным воздухом вместе с этим столбиком ртути:
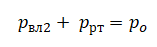
Причем ртуть находится в жидком состоянии, следовательно, ее давление может найти как давление в жидкостях:
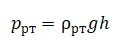
Вместо высоты мы можем применить высоту столбика ртути (l):
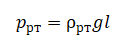
Следовательно:

Или:
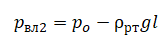
Также учитываем, что давление влажного воздуха и столбика ртути равно атмосферному давлению, которое может быть определено как произведение плотности ртути на ускорение свободного падения и высоту ртутного столба при таком давлении (обозначим за H):
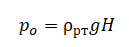
Так как в условии сказано, что атмосферное давление равно 760 мм рт. ст., то высота ртутного столба в данном случае может быть принята за 760 мм.
В случаях 1 и 2 температура остается неизменной. Следовательно, речь идет об изотермическом процессе, для которого применим закон Бойля — Мариотта:
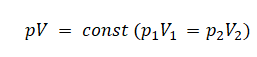
Объем влажного воздуха можем считать как произведение площади сечения трубки на высоту столбика с влажным воздухом. Тогда закон Бойля — Мариотта принимает вид:
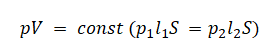
Площадь сечения остается неизменной величиной, поэтому ее обозначаем без индекса. Следовательно, объем влажного воздуха при изменении положения трубки меняется так же, как меняется длина столбика с этим воздухом:
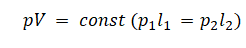
Давления влажного воздуха в случаях 1 и 2 мы выразили выше (они обозначены как (function(){function i(e){seraph_pds.View.InitFormulas();}if(seraph_pds && seraph_pds.View)i();else document.addEventListener(‘DOMContentLoaded’,i);})()pвл1 и pвл2 соответственно). Подставим их в выражение выше и преобразуем его:
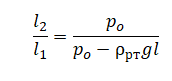
Основное уравнение идеального газа (а мы будем считать влажный воздух в трубке идеальным):
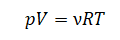
Или:
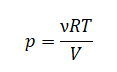
Применим его для влажного воздуха и получим:
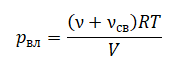
ν — количество моль водяного пара в трубке, νсв — количество моль сухого воздуха в трубке.
Так как речь идет об изотермическом процессе:
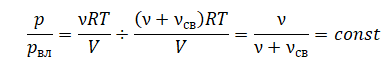
Поэтому отношение давлений водяных паров в 1 и 2 случае равно отношению давлений влажного воздуха в 1 и 2 случае:
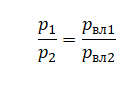
Отсюда имеем:
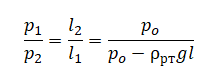
Теперь подставим это в следующее выражение:
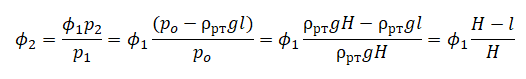
Отсюда:
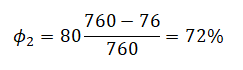
Ответ: 72
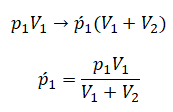
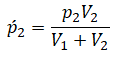
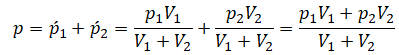
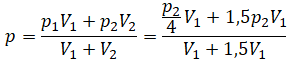
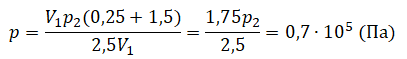

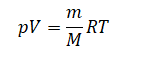
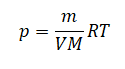
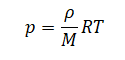
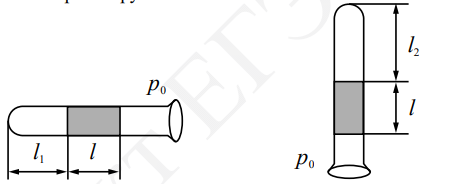
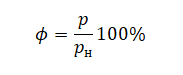
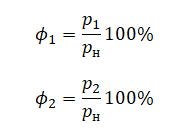
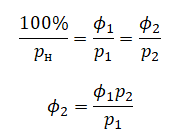

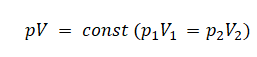
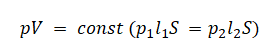
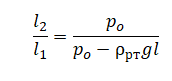
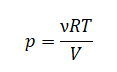
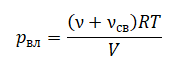
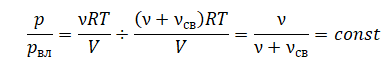
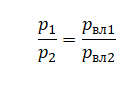
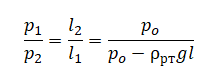
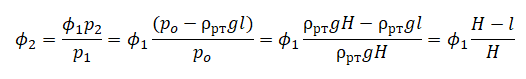
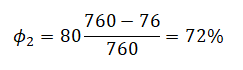
 В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?
В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?