Электромагнитная индукция и магнитный поток | теория по физике 🧲 магнетизм

Английский физик и химик Майкл Фарадей считал, что если электрический ток может намагнитить кусок железа, то магнит тоже каким-то образом должен вызывать появление электрического тока. И он оказался прав. В 1831 году он открыл явление электромагнитной индукции.

Определение

Электромагнитная индукция — явление, заключающееся в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитной поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.

Опыты Фарадея

Сначала Фарадей открыл электромагнитную индукцию в неподвижных друг относительно друга проводниках пи замыкании и размыкании цепи. Он собрал установку, состоящую из источника тока, реостата, гальванометра, ключа и двух катушек. Одну катушку он соединил с реостатом, ключом и подключил к источнику питания. Вторую он подключил к гальванометру и устанавливал ее на тот же сердечник, что и первую. Всякий раз, как он замыкал или размыкал цепь, стрелка гальванометра отклонялась от нулевого значения шкалы.

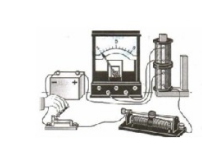
Затем электромагнитная индукция была обнаружена при сближении и удалении катушек в замкнутой цепи. Если ученый перемещал одну катушку относительно второй, стрелка гальванометра также отклонялась.

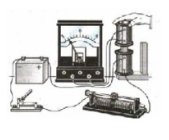
Потом явление электромагнитной индукции было обнаружено при изменении силы тока в подключенной к источнику питания катушке с помощью реостата. Если сила тока уменьшалась или увеличивалась, стрелка гальванометра отклонялась от начального положения. Но она вставала на нулевое значение, если прекращать перемещение ползунка реостата (делать силу тока постоянной).

Ученый понимал, что магнит представляет собой совокупность маленьких токов, циркулирующих в молекулах. Поэтому он поставил следующий опыт.

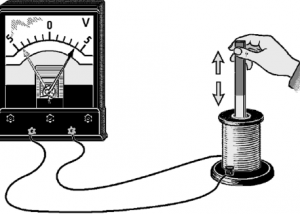
Фарадей собрал установку, состоящую из катушки и подключенного к ней гальванометра. Затем он взял полосовой магнит и ввел его внутрь катушки. В этот момент стрелка амперметра отклонилась от нулевого значения. Если же ученый останавливал движение магнита внутри катушки, стрелка прибора возвращалась в исходное положение. При извлечении магнита из катушки стрелка амперметра отклонялась в противоположную сторону.

Все эти опыты позволили Фарадею уловить то общее, от чего зависит появление индукционного тока в катушках. В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. При этом причина изменения числа линий магнитной индукции совершенно безразлична. Это может быть изменение числа линий магнитной индукции, пронизывающих поверхность неподвижного проводящего контура вследствие изменения силы тока в соседней катушке, и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве.

Магнитный поток

Вектор магнитной индукции $\to B$ характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значения вектора $\to B$ не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром. Для этого рассмотрим плоский замкнутый проводник (контур) с площадью поверхности S, помещенный в однородное магнитное поле. Нормаль $\to n$ к плоскости проводника составляет угол α с направлением вектора магнитной индукции $\to B$ (см. рисунок).

Определение

Магнитным потоком, или потоком магнитной индукции через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции $\to B$ на площадь S и косинус угла α между векторами $\to B$ и $\to n$ . Обозначается магнитный поток как $Φ .$

$Φ = B S cos . α$

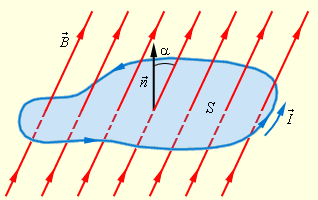
Произведение $B cos . α = B_{n}$ представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому:

$Φ = B_{n} S$

Магнитный поток можно представить как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единица измерения магнитного потока — вебер (Вб). Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции.

Пример №1. Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м² под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?

Выразим модуль вектора магнитной индукции:

$В = \frac{Φ}{S cos . α}$

Так как нам дан угол между поверхностью рамки и вектором магнитной индукции, угол между вектором магнитной индукцией и нормалью будет равен разности 90^о и угла поверхностью рамки и вектором магнитной индукции. Отсюда:

$\frac{0, 2}{0, 5 cos . (90 ° - 30 °)} = \frac{0, 2}{0, 5 \cdot 0, 5} = 0, 8 (Т л)$

Текст: Алиса Никитина, 8.7k 👀

Задание EF18180

Плоская рамка помещена в однородное магнитное поле, линии магнитной индукции которого перпендикулярны её плоскости. Если площадь рамки увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза, то магнитный поток через рамку

Ответ:

а) увеличится в 9 раз

б) не изменится

в) уменьшится в 3 раза

г) уменьшится в 9 раз

Алгоритм решения

1.Записать формулу, раскрывающую зависимость магнитным потоком, площадью рамки, помещенной в магнитное поле и индукции этого поля.

2.Установить, как изменится магнитной поток при изменении указанных в задаче величин.

Решение

Магнитный поток, пронизывающий площадь, ограниченную рамкой, определяется формулой:

$Φ = B S cos . α$

По условию задачи площадь рамки увеличивают в 3 раза, а индукцию магнитного поля уменьшают во столько же раз. Следовательно:

$S_{1} = 3 S$

$B_{1} = \frac{B}{3}$

Следовательно:

$Φ_{1} = B_{1} S_{1} cos . α = 3 S \cdot \frac{B}{3} cos . α = B S cos . α = Φ$

Следовательно, магнитный поток не изменится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18285

Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м² под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?

Ответ:

а) 0,2 Тл

б) 0,4 Тл

в) 0,8 Тл

г) 0,16 Тл

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения потока магнитной индукции.

3.Выразить искомую величину.

4.Подставить исходные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Магнитный поток, пронизывающий рамку:

Φ

= 0,2 Вб.

• Площадь рамки, находящейся в однородном магнитном поле: S = 0,5 м².

• Угол между вектором магнитной индукции и плоскостью, ограниченной контуром рамки:

β

= 30^о.

Запишем формулу для определения потока магнитной индукции:

$Φ = B S cos . α$

Так как в условиях задачи указан угол между вектором магнитной индукции и плоскостью рамки, то угол между нормалью и плоскостью рамки будет равен $α = 90 ° - β$ .

Выразим модуль вектора индукции магнитного поля:

$B = \frac{Φ}{S cos . (90 - β)} = \frac{0, 2}{0, 5 \cdot cos . (90 ° - 30 °)} = \frac{0, 4}{0, 5} = 0, 8 (Т л)$

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19000

Проволочная рамка площадью 2×10^–3м²вращается в однородном магнитном поле вокруг оси, перпендикулярной вектору магнитной индукции. Магнитный поток, пронизывающий площадь рамки, изменяется по закону Ф=4×10^–6cos10πt, где все величины выражены в СИ. Чему равен модуль магнитной индукции? Ответ выразите в мТл.

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения потока магнитной индукции.

3.Выразить искомую величину.

4.Подставить исходные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Магнитный поток, пронизывающий рамку:

Φ

= 4∙10^–6cos10πt Вб.

• Площадь рамки, находящейся в однородном магнитном поле: S = 2∙10^–3 м².

Запишем формулу для определения потока магнитной индукции:

$Φ = B S cos . α$

Выразим модуль вектора индукции магнитного поля:

$B = \frac{Φ}{S cos . α}$

Так как рамка вращается в однородном магнитном поле, угол между нормалью, проведенной к ее плоскости, и вектором магнитной индукции постоянно меняется. Если мы примем этот угол за 0 градусов, то косинус этого угла будет равен 1. Тогда мы получим максимальное значение магнитного потока, пронизывающего рамку, и сможем вычислить модуль вектора магнитной индукции.

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

Опыты Фарадея

Магнитный поток

Задание EF18180

Задание EF18285

Задание EF19000

ЕГЭ по физике

Вся теория

Добавить комментарий Отменить ответ