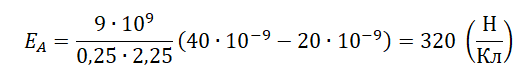Принцип суперпозиции сил и полей | теория по физике 🧲 электростатика

Принцип суперпозиции сил

Определение

Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:

$- R = \sum {- F}_{i}$

F_i — сила, с которой электрическое поле зарядом q действует на пробный заряд q_i, помещенный в это поле на расстоянии r_i от этого заряда. Численно ее можно вычислить по формуле:

$F_{i} = \frac{k q_{i} q}{r_{i}^{2}}$

Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):

Сделать чертеж. Указать расположение всех зарядов и их знаки.
Выделить заряд, для которого определяют равнодействующую.
Пронумеровать остальные заряды.
Определить расстояния от выделенного заряда до всех остальных.
Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.

Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила ${- F}_{K},$ действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?

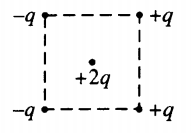
Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.

Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:

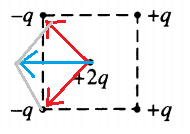
Из рисунка видно, что кулоновская сила ${- F}_{K},$ действующая на положительный точечный электрический заряд +2q, направлена влево.

Принцип суперпозиции полей

Определение

Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:

$- E = \sum {- E}_{i}$

${- E}_{i}$ — напряженность, создаваемая зарядом $q_{i}$ в точке, находящейся на расстоянии $r_{i}$ :

${- E}_{i} = \frac{k q_{i}}{r_{i}^{2}}$

Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:

$φ = \sum φ_{i}$

$φ_{i}$ — потенциал электростатического поля, создаваемого зарядом $q_{i}$ на расстоянии $r_{i}$ от него. Численно он равен:

$φ_{i} = \pm \frac{k q_{i}}{r_{i}}$

Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:

$W_{p} = \sum W_{i p}$

$W_{i p}$ — потенциальная энергия взаимодействия зарядов $q_{i}$ и $q_{n}$ , находящихся на расстоянии $r_{i}$ друг от друга. Численно она равна:

$W_{i p} = \pm \frac{k q_{i} q_{n}}{r_{i}}$

Примеры определения расстояний

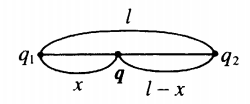	Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними: $r_{1} = x; r_{2} = l - x$
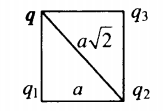	Изучаемый заряд лежит в вершине квадрата со стороной a: $r_{1} = r_{3} = a; r_{2} = a \sqrt 2$
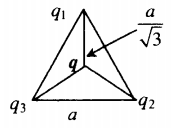	Изучаемый заряд лежит в центре равностороннего треугольника со стороной a: $r_{1} = {r_{2} = r}_{3} = \frac{a}{\sqrt 3}$
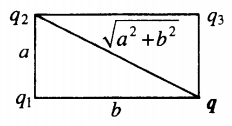	Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b: $r_{1} = b; r_{2} = \sqrt{a^{2} + b^{2}}; r_{3} = a$
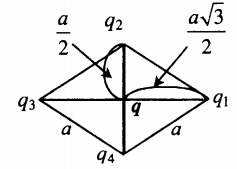	Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120^о: $r_{1} = r_{3} = \frac{a \sqrt 3}{2}; r_{2} = r_{4} = \frac{a}{2}$
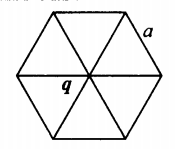	Изучаемый заряд лежит в центре правильного шестиугольника со стороной a: $r_{1} = r_{2} = r_{3} = r_{4} = r_{5} = r_{6} = a$

Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.

Построим чертеж:

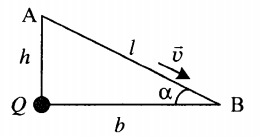
Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):

$E_{A} = E_{B}$

Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:

$E_{A} = m g h + \frac{k q Q}{h}$

В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:

$E_{B} = \frac{m v^{2}}{2} + \frac{k q Q}{b}$

Расстояние между точкой В и местом, где находится заряд Q:

$b = \frac{h}{tan . α}$

Приравняем правые части уравнений:

$m g h + \frac{k q Q}{h} = \frac{m v^{2}}{2} + \frac{k q Q}{b}$

$m g h + \frac{k q Q}{h} = \frac{m v^{2}}{2} + \frac{k q Q tan . α}{h}$

$\frac{m v^{2}}{2} = m g h + \frac{k q Q}{h} - \frac{k q Q tan . α}{h} = m g h + \frac{k q Q}{h} (1 - tan . α)$

$v = \sqrt{\frac{2 (m g h + \frac{k q Q}{h} (1 - tan . α))}{m}} = \sqrt{2 g h + \frac{2 k Q}{m h} (1 - tan . α)}$

Текст: Алиса Никитина, 4.6k 👀

Задание EF17563

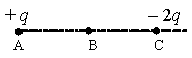Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?

Ответ:

а) − 5q

б) − 4q

в) 4q

г) 5q

Алгоритм решения

1.Определить направление вектора напряженности для зарядов в точках А и С.

2.Определить напряженность поля в точке В, используя принцип суперпозиции.

3.Найти, какой заряд нужно поместить в точку С вместо имеющегося, чтобы напряженность электростатического поля в точке В увеличилась вдвое.

Решение

Вектор напряженности заряда в точке А направлен в направлении от этого заряда, так как он положительный. Это значит, что в точке В вектор напряженности E_A направлен вправо. Вектор напряженности заряда в точке С направлен к этому заряду, так как он отрицательный. Поэтому в точке В вектор напряженности E_C тоже направлен вправо. Следовательно, при векторном сложении модули напряженностей должны складываться:

$E = E_{A} + E_{C} = \frac{k | q |}{r^{2}} + \frac{k | - 2 q |}{r^{2}} = \frac{3 k q}{r^{2}}$

Найдем, какой нужно поместить заряд в точку С, чтобы напряженность увеличилась вдвое:

$\frac{k | q |}{r^{2}} + \frac{k | x |}{r^{2}} = 2 \cdot \frac{3 k q}{r^{2}} = \frac{6 k q}{r^{2}}$

Преобразуем выражение и получим:

$| q | + | x | = 6 q$

Отсюда:

$| x | = 5 q$

Этот заряд должен быть отрицательным, так как в этом случае линии напряженности поля, создаваемого зарядом в точке С, будут складываться с линиями напряженности поля, создаваемыми положительным зарядом в точке А. Следовательно, x = –5q.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17967

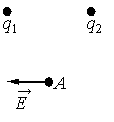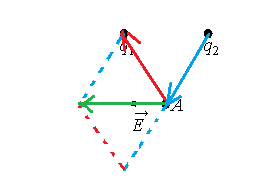
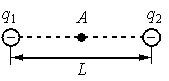На рисунке показано направление вектора напряжённости электрического поля E в точке А, равноудалённой от равных по модулю точечных зарядов q₁ и q₂. Какие знаки имеют заряды?

Ответ:

а) q₁ > 0; q₂ < 0

б) q₁ < 0; q₂ > 0

в) q₁ > 0; q₂ > 0

г) q₁ < 0; q₂ < 0

Алгоритм решения

1.Вспомнить, как направлены векторы напряженности полей, созданных положительным и отрицательным зарядами.

2.Построить параллелограмм, сторонами которого являются отрезки, равные длинам векторов напряженности полей, создаваемыми двумя точечными зарядами.

3.Определить, какое направление должны иметь векторы напряженности, чтобы результатом их вычитания/сложения был вектор

- E

.

4.Определить знаки зарядов с учетом направления векторов напряженности полей.

Решение

Векторы напряженности электростатического поля, создаваемого положительным точечным зарядом, направлены по радиусным линиям от заряда. Векторы напряженности электростатического поля, создаваемого отрицательным точечным зарядом, направлены по радиусным линиям к заряду.

Построим параллелограмм. Чтобы получить вектор $- E$ , нужно вычесть из вектора ${- E}_{1}$ вектор ${- E}_{2}$ . Причем первый должен быть направлен в сторону заряда, а второй — от заряда.

Следовательно, заряд q₁ отрицательный (q₁< 0), а заряд q₂ положительный (q₂ > 0).

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18357

Два точечных отрицательных заряда: q₁=−20 нКл и q₂=−40 нКл находятся в вакууме на расстоянии L=1,5м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов.

Ответ:

а) 160 Н/Кл

б) 320 Н/Кл

в) 125 Н/Кл

г) 640 Н/Кл

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Определить направление векторов напряженности в точке А.

3.Выполнить общее решение задачи, применив принцип суперпозиции полей.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Величина первого заряда: q₁ = –20 нКл.

• Величина второго заряда: q₂ = –40 нКл.

• Расстояние между зарядами: L = 1,5 м.

–20 нКл = –20∙10^–9Кл

–40 нКл = –40∙10^–9Кл

Вектор напряженности поля, создаваемого первым зарядом в точке А, направлен влево (в сторону заряда), так как он отрицательный. Второй заряд тоже отрицательный, но он лежит по другую сторону от точки А. Поэтому в ней вектор напряженности поля, создаваемого вторым зарядом, будет направлен вправо. Так как модуль второго заряда больше модуля первого, результирующая напряженность будет направлена вправо. Напряженность в точке А в этом случае будет вычисляться как разность двух напряженности:

$E_{A} = E_{2} - E_{1}$

Напряженность определяется формулой:

$E = \frac{k | q |}{r^{2}}$

Следовательно:

$E_{A} = \frac{k | q_{2} |}{{(0, 5 L)}^{2}} - \frac{k | q_{1} |}{{(0, 5 L)}^{2}} = \frac{k}{{(0, 5 L)}^{2}} (| q_{2} | - | q_{1} |)$

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

ЕГЭ по физике

Вся теория

• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •