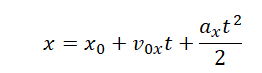Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с2. Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v0 = 0 м/с.
В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.
Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t1 = 0 с, а t2 = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает вид:

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с2, достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:


В результате получаем два корня: t1 = 0,6 с, а t2 = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.