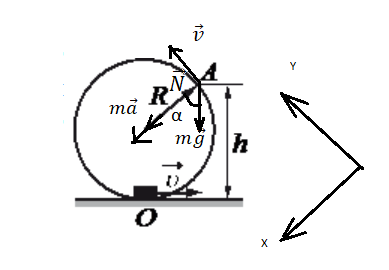
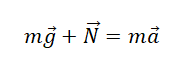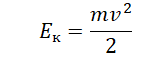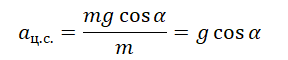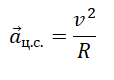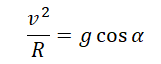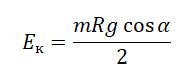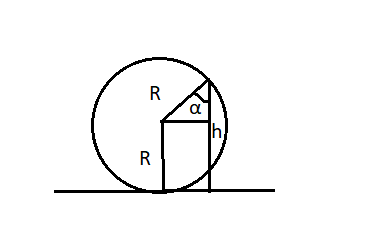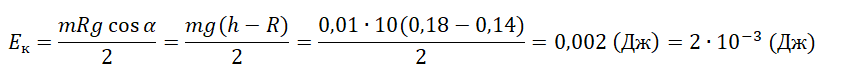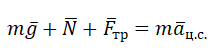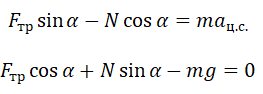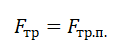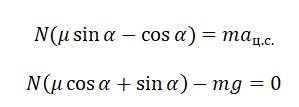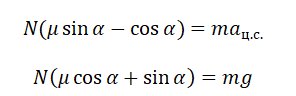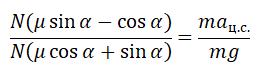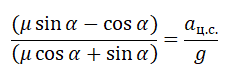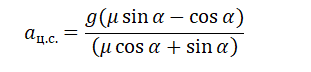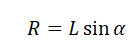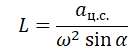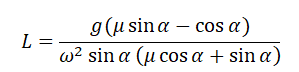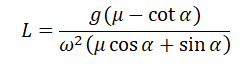На тело, движущееся по окружности, действует множество сил. При описании его движения нужно учесть все силы и правильно определить их направление. В этом вам поможет таблица:
| Сила | Направление |
| Сил тяжести | Вертикально вниз |
| Сила реакции опоры | Перпендикулярно опоре |
| Сила натяжения нити | Вдоль оси подвеса |
| Сила упругости | Противоположно деформации |
| Сила трения | Противоположно направлению движения или возможного движения |
| Сила сопротивления | |
| Центростремительная сила | К центру окружности |
Алгоритм решения задач на движение тела по окружности с постоянной по модулю скоростью
Частные случаи движения тела по окружности
Автомобиль на повороте |
|
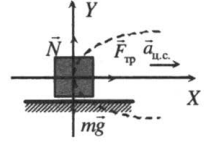 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = maц.с. |
|
| Проекция на ось ОХ: | |
|
Fтр = maц.с. |
|
| Проекция на ось ОУ: | |
|
N – mg = 0 |
|
Тело на вращающемся диске |
|
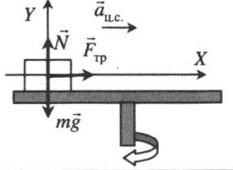 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = maц.с. |
|
| Проекция на ось ОХ: | |
|
Fтр = maц.с. |
|
| Проекция на ось ОУ: | |
|
N – mg = 0 |
|
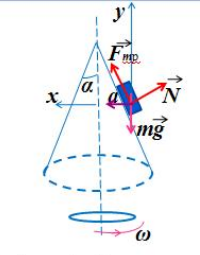
Конический маятник |
|
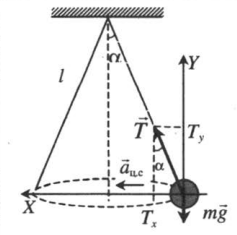 |
Второй закон Ньютона в векторной форме: |
|
T + mg = maц.с. |
|
| Проекция на ось ОХ: | |
|
T sinα = maц.с. |
|
| Проекция на ось ОУ: | |
|
T cosα – mg = 0 |
|
| Учтите, что: mg tgα = maц.с. | |
| Радиус окружности, по которой происходит движение тела: R = l sinα | |
Пример №1. Автомобиль совершает поворот на горизонтальной дороге по дуге окружности. Каков минимальный радиус окружности траектории автомобиля при его скорости 18 м/с и при коэффициенте трения шин о дорогу 0,4?
Проекция сил, действующих на автомобиль, на проекцию ОХ в данном случае равна:
Fтр = maц.с.
Выразим силу трения через силу реакции опоры:
μN = maц.с.
μmg = maц.с.
После взаимоуничтожения масс остается:
aц.с. = μg
Также известно, что центростремительное ускорение определяется формулой:
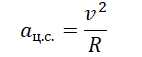
Приравняем правые части уравнений:
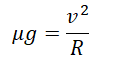
Выразим радиус окружности, по которой движется автомобиль:
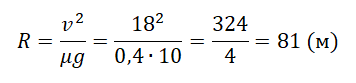
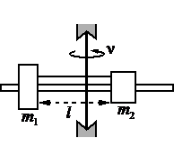 На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.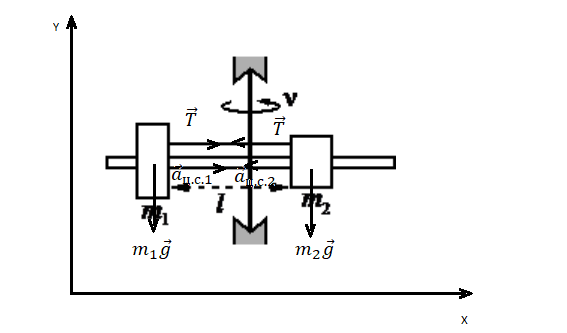
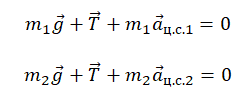
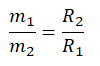
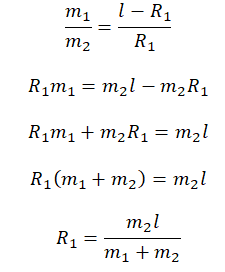
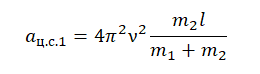
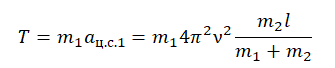
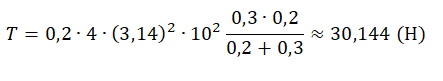
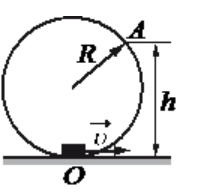 Небольшая шайба массой
Небольшая шайба массой